迭代与递归:To Iterate,Human; to Recurse, Divine.
引言
从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?「从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?『从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?……』」
什么是递归
递归(Recursion),在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。
为什么要用递归
- 有些问题很难用一般的循环来解决,采用递归使得我们思考的方式得以简化。
- 递归可以处理无限循环问题。(例如对于一个 字符串进行全排列 ,字符串长度不定)
void permute(const string &prefix, const string &str) { if(str.length() == 0) cout << prefix << endl; else { for(int i = 0; i < str.length(); i++) permute(prefix+str[i], str.substr(0,i)+str.substr(i+1,str.length())); } }
递归基本思想
- 把规模大的问题转化为规模小的 相似 的子问题来解决。
- 解决大问题的方法和解决小问题的方法往往是同一个方法。
递归使用条件
- 存在一个递归调用的 终止条件 ;
- 每次递归的调用必须 越来越靠近终止条件 ;只有这样递归才会终止,否则是不能使用递归的!
递归过程理解
- 我们已经完成了吗?如果完成了,返回结果。
- 如果没有,则简化问题,解决较容易的问题,并将结果组装成原始问题的解决办法。
return 语句
下面将会在解释递归深度为N层的递归函数的具体执行过程,在这之前,先回忆一下 “return”语句,因为递归一般都是使用return语句进行处理。
return语句用于结束当前正在执行的函数,并将控制权返回给调用此函数的函数。
return语句有两种形式:
- “ return; ”
不带返回值的return语句只能用于返回类型为void的函数。
一般情况下使用不带返回值的return语句是为了引起函数的强制结束。
隐式的return发生在函数的最后一个语句完成时。
- “ return expression; ”
任何返回类型不是void的函数都必须返回一个值, 返回值的类型必须和函数的返回类型相同,或者能隐式转化为函数的返回类型。
递归函数
递归函数一般可以分为三个部分:
- 递归调用前的处理
- 递归函数本身
- 递归调用后的处理
即:
recursion(){
//block1:递归调用前的处理
code before recursion
{
do something;
}
//block2:调用递归函数本身
{
if(end_condition) //递归终止条件
{
end;
}
else
{
recursion();
}
}
//block3:递归调用后的处理
code after recursion
{
do something;
}
}//end of recursion在解释上述代码之前,对于递归首先必须理解如下几点:
- 每一次函数调用都会有一次返回,显式的return语句返回或者隐式的执行完最后一条语句之后返回。
- 位于递归函数入口 前 的语句,由 最外层往最里层 执行。
- 位于递归函数入口 后 的语句,由 最里层往最外层 执行。
- 当程序流执行到某一级递归的结尾处时(执行完block3),它会转移到前一级递归继续执行
上述代码的具体执行过程为(假设递归深度为N):
- 执行第1层的block1;
- 执行第1层的block2;
- 执行第2层的block1;
- 执行第2层的block2;
... ...
执行第N层的block1;
执行第N层的block2时,由于满足end_condition,不再调用递归函数
执行第N层的block3。
转移到前一级的递归处
执行第N-1层的block3;
执行第N-2层的block3;
... ...
执行第2层的block3;
执行第1层的block3;
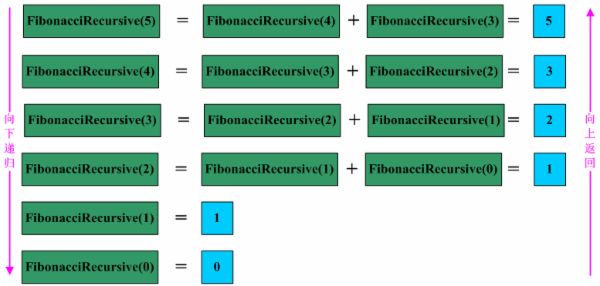
对于Fibonacci函数
int Fib(int n)
{
if( n < 2)
return n;
return (Fib(n-1)+Fib(n-2));
}递归应用:
- 把问题规模递归到最小 :递归在处理类似T(n)=aT(n/b)+f(n)的问题上的应用,如数据的定义是按递归定义的(Fibonacci函数,n的阶乘),问题解法按递归实现(分治,回溯)。
处理方法: 展开递归 直到可以 直接求解问题 ,在递归 “返回过程” 中求解每步中未解决部分的问题
recursion(T(n)) //T(n)为问题规模
{
展开递归,直到可以直接求解问题:
if (end_condition) //end_conditon:可以直接求解问题的T(n),如问题规模为1,2
{
return expression;
}
else
{
return_value = recursion(g(f(n)));//继续展开,g(f(n))的规模小于f(n)的规模
return solve(return_value);//solve()求解每步中未解决的部分,这部分求解依赖规模较小问题的解。
上面两部步就相当于Fib函数中的return (Fib(n-1)+Fib(n-2));
}
}
- 将问题递归穷举其所有的情形 ——递归在处理不确定数量的嵌套循环中的应用,如处理数据结构本身是按递归定义的树,图等问题,不能用循环实现,只能使用递归。
处理方法: 展开递归 ,在递归 “展开过程” 中求解问题:
recursion(T(n))
{
展开递归,直到满足终止条件:
if (end_condition)//end_condition:递归已经展开完毕,即已穷举问题的所有情形
{
return;
}
在展开过程中的每一步都解决该步中的问题。
solve(T(n));
recursion(g(f(n))); //继续展开;
}求解递归式
求解递归式一般有3种方法:
代入法
猜测一个界,然后用数学归纳法证明这个界是正确的。
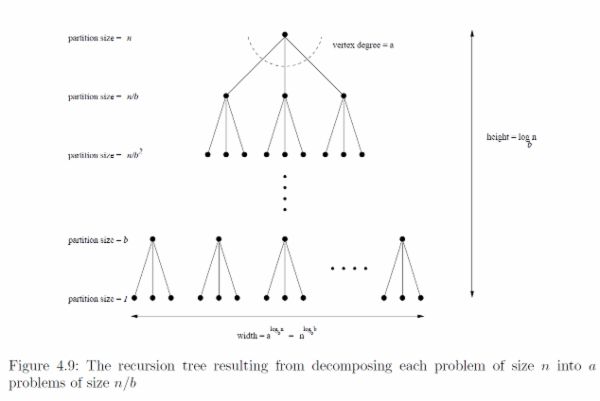
递归树法
将递归式转换为一棵树,其节点表示不同层次的递归调用产生的代价。
- 在递归树中 每个节点表示一个单一子问题的代价 ,子问题对应某次递归调用。
- 将 树中每层中的代价求和 ,得到每层的代价,然后将 所有层的代价求和 ,得到所有层次的递归调用的总代价
主方法
求解形如T(n)=aT(n/b)+f(n)的递归式的界。
递归式描述的是这样一种算法的运行时间:
它将规模为n的问题分解为a个子问题,每个子问题的规模为n/b,其中a,b都是正常数。a个子问题递归地进行求解,每个花费时间T(n/b)。 函数f(n)包含了问题分解和子问题合并的代价 。
严格讲上述递归式并不是良好定义的,因为n/b并不一定是整数,但将a项T(n/b)都替换为T(⌊n/b⌋)或T(⌈n/b⌉)并不影响递归式的渐进分析。
主方法求解依赖下面的定理: 
主定理不能适合于这样的递归式:T(n)=2T(n/2)+nlgn,因为该递归式落入了情况2和情况3之间的间隙。
对于所有递归式,只需 计算 ![]() 并和f(n)比较 即可。
并和f(n)比较 即可。
如:
T(n)=2T(n/2)+O(n) ---> O(nlgn)
T(n)=2T(n/2)+O(lgn) ---> O(n)
如何书写递归式
书写递归式主要的难点在于确定f(n), 函数f(n)包含了问题分解和子问题合并的代价 ,下面几个公式概括了常见的递归处理形式。
公式1
如果递归程序 循环处理 输入, 每次减少一项 ,则递归式为:T(n)=T(n-1)+n。T(N)=N*N/2
公式2
如果递归程序 每一步处理一半的输入 (另一半输入不需要考虑,如二分查找),则递归公式为:T(n)=T(n/2)+1。T(N)=lgN
公式3
如果递归程序 每一步处理一半的输入 ,但需要 检查输入的每一项 ,则递归公式为:T(n)=T(n/2)+n。T(N)=2N
公式4
如果递归程序 每一步将输入分成两半 ,但在划分之前、划分过程中或划分之后 需要线性地遍历输入 ,则递归公式为:T(n)=2T(n/2)+n。T(N)=NlgN
公式5
如果程序 每一步将输入分成两半 ,并且需要 做一些其他处理 (消耗常数时间),则递归公式为:T(n)=2T(n/2)+1。T(N)=2N
递归类型:
- Tail recursion:
当递归调用是整个函数体中 最后执行的语句 ,且 它的返回值不属于表达式的一部分 时,这个递归调用就是尾递归。即如下这种形式的递归:
```c
foo(){
something else;
return foo()//最后执行的语句,且不属于任何表达式的一部分
}
求解最大公约数的算法就是一个最典型的尾递归:
```c
int GCD(int ,int y)
{
if(y == 0)
return x;
else
return GCD(y, x % y);
}普通递归的实现:
普通递归的实现是通过调用函数本身, 每次调用函数本身要保存局部变量、形参、调用函数地址、返回值 。如果递归调用N次,就要分配N 局部变量、N 形参、N 调用函数地址、N 返回值这个执行过程的开销往往很大。当递归深度很大时,往往会导致栈溢出。
尾递归的实现:
尾递归特点是在递归返回过程中不用做任何操作 ,大多数现代的编译器会利用这种特点自动生成优化的代码。当编译器检测到一个函数调用是尾递归的时候,它就 覆盖当前的活跃记录而不是在栈中去创建一个新的 。通过覆盖当前的栈帧而不是在其之上重新添加一个,这样所使用的栈空间就大大缩减了,这使得实际的运行效率会变得更高。
因此,只要有可能我们就需要将递归函数写成尾递归的形式。
采用尾递归实现Fibonacci函数:
int Fib(int n,int ret1,int ret2)//ret1,ret2为数列的开头两项
{
if(n==0)
return ret1;
return Fib(n-1,ret2,ret1+ret2);
} (原理:0 1 1 2 3 5 8 13 21 ... F(8)=23,变换后为1 (0+1) 2 3 5 8 13 21 ... F(7)=23)
函数执行过程如下: 
- Augmenting recursion:
Whenever there is a pending operation to be performed on return from each recursive call, then recursion is known as Augmenting recursion.
The "infamous" factorial function fact is usually written in a non-tail-recursive manner:
int fact (int n)
{
if (n == 0) return 1;
return n * fact(n - 1);
}- Direct Recursion:
A function foo is directly recursive if it contains an explicit call to itself .int foo(int x) { if (x <= 0) return x; return foo(x - 1); } - Indirect Recursion:
A function foo is indirectly recursive if it contains a call to another function which ultimately calls foo .int foo(int x) { if (x <= 0) return x; return foo1(x); } int foo1(int y) { return foo(y - 1); } - Mutual Recursion:
When the pair of functions contains call to each other then they are said to perform mutual recursion.int foo(int x) { if (x <= 0) return x; return foo1(x); } int foo1(int y) { return foo(y - 1); } - Linear Recursion:
A recursive function is said to be linearly recursive when no pending operation involves another recursive call to the function .
For example, the "infamous" fact function is linearly recursive.
int fact (int n)
{
if (n == 0) return 1;
return n * fact(n - 1);
}
The pending operation is simply multiplication by a scalar, it does not involve another call to fact- Tree or Non-Linear Recursion:
A recursive function is said to be tree recursive (or non-linearly recursive) when the pending operation does involve another recursive call to the function .
```c
The Fibonacci function fib provides a classic example of tree recursion.
int fib(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
return fib(n - 1) + fib(n - 2);
}
Notice that the pending operation for the recursive call is another call to fib. Therefore fib is tree-recursive.
递归VS迭代
先解释一下以下几个概念:
循环(loop) ,一段在程序中只出现一次,但可能会连续运行多次的代码(不变的重复)。比如,while语句。
迭代(iterate) ,反复地运用同一函数计算,前一次迭代得到的结果被用于作为下一次迭代的输入(变化的循环)。指的是按照某种顺序逐个访问列表中的每一项。比如,for语句。
遍历(traversal) ,指的是按照一定的规则访问树形结构中的每个节点,而且每个节点都只访问一次。
递归(recursion) ,指的是一个函数不断调用自身的行为。比如斐波纳契数列。
使用递归的场景:
- 问题较复杂,使用递归可以简洁的解决
-
问题本身有递归的含义,如树的遍历
使用迭代的场景:
使用递归的场景
- Quick Sort
- Merge Sort
- All N-Log Sort
- Tree traversals
- XML Parsers
- HTML Parsers
- Backtracking Algorithm
- Binary Space Partitioning (BSP) Trees used for collision detection in
game development. - Recursive-descent language parsers
- Simulating state machines
- Lists (Linked Lists)
- Graphs
- Inductive reasoning used in AI
- Fractals
参考
Introduction to Algorithms
Algorithmrithms in C++ Parts 1-4
http://www.codeproject.com/Articles/32873/Recursion-made-simple
http://www.nowamagic.net/librarys/veda/detail/2314