神经网络详细解释（包含BP算法的推导）

神经网络是在人工智能界是比较流行的一种模型。发展到今日已经有很多变种，想cnn，rnn，LSTM，对抗神经网络，等等很多网络结构，网上也有很多比较详细的解释，最近系统的学习了一下神经网络，包括网络结构细节，激活函数，正向传播，反向传播的推导，梯度的计算，过拟合的解决方式等等，想要系统的学习神经网络的同学看过来吧。嘿嘿！

单层神经网络结构

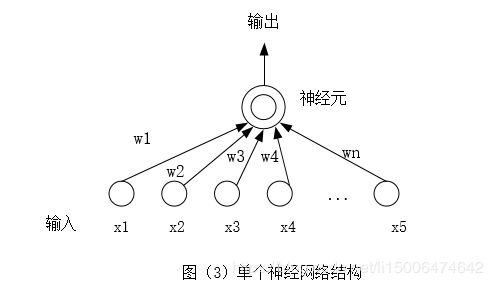
先从最简单的开始理解神经网络，如图（1），这是一个最简单的神经网络结构

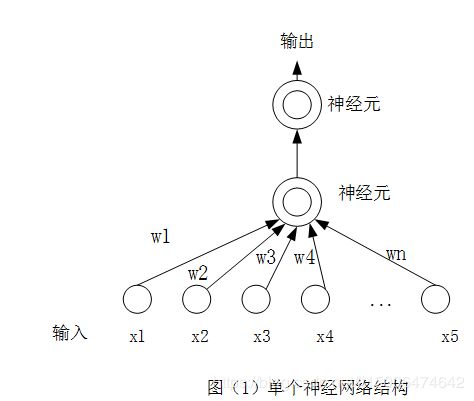
输入为：x1，x2，….xn。每个输入都对应一个权重w，那么将数据集x输入到神经元里面会有什么操作呢？如图（2）

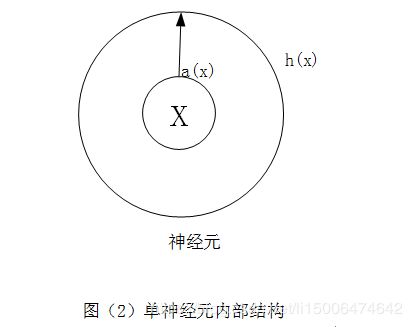
数据X输入到神经元后会经过两个操作：“a(x)”,和”h(x)” 后才能输出到下一个神经元中。我们也把a(x)称为pre-activation，h(x)称为post-activation，也就是第一步和第二步的意思。我们先看第一步a（x），a(x)是指对利用权重对数据进行一次线性转换，如公式（1）

简单来说就是将输入集乘以对应权重加上一个偏置。
第二步h（x）是指的对a（x）进行一次非线性的转换，如公式（2）

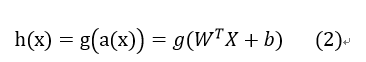
g(x)指的是激活函数，也就是对数据进行非线性转换的函数。如tanh，sigmold，relu等

那么问题来了，为什么要进行非线性的转换？

假设我们去掉h(x)这一步，每个神经元只经过a（x）也就是只有线性转换，那么我们的数据从第一个神经元到下一个神经元的过程就是$a_1\left(a\left(x\right)\right)=w_1^T\left(a\left(x\right)\right)+b_1$再到下一个神经元为：$a_2\left(a_1\left(a\left(x\right)\right)\right)=W_2^T{a}_1\left(a\left(x\right)\right)+b_2$

假定到此结束准备输出，我们展开公式：
$a_2\left(a_1\left(a\left(x\right)\right)\right)=W_2^T{a}_1\left(a\left(x\right)\right)+b_2=W_2^T\left(W_1^{T}a\left(x\right)+b_1\right)+b_2=W_2^T\left(W_1^T\left(W^{T}X+b\right)+b_1\right)+b_2=W_2^T{W}_1^T{W}^{T}X+W_2^T{W}_1^{T}b+W_2^T{b}_1+b_2$

由于W和b是常数，因此$W_2^T{W}_1^T{W}^{T}X$可以写成$W_c^{T}X$，还有$W_2^T{W}_1^{T}b+W_2^T{b}_1+b_2$可以写成$b_c$这样公式就可以写成:
$a_2\left(a_1\left(a\left(x\right)\right)\right)=W_c^{T}X+b_c$

这样大家就会发现我们加这么多层神经元是没有意义的，最后还是变成一层的样子，所以我们在a(x)后加了非线性转换h(x)这样保证每层都是有意义的。因此激活函数比较的选择也是比较重要的

有意思的现象

如图（3）当单层神经网络，只有一个神经元并且激活函数是sigmold时，是此时$a(x)=W^{T}X+b$，
$g\left(x\right)=\frac{1}{1+e^{-x}}$
那么此时：
$输出=h\left(x\right)=g\left(w^{T}x+b\right)=\frac{1}{1+e^{-(w^{T}x+b)}}$

而逻辑回归为：
$p(y|x)=\frac{1}{1+e^{-(w^{T}x+b)}}$

所以说逻辑回归是神经网络的一个特例

常见的激活函数：

Linear activation（线性激活函数）

公式：$g\left(a\right)=a$

直接输出，没有任何意义，没有边界，输出多层相当于一层
Sigmold函数：

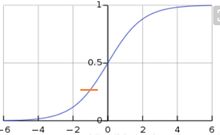
公式：$g\left(a\right)=\frac{1}{1+e^{-a}}$

将输入映射到(0,1)之间 严格递增的函数

Tanh函数:：

公式：$y\left(a\right)=\tanh \left(a\right)=\frac{e^a-e^{-a}}{e^a+e^{-a}}$

将输入映射到(1,-1)之间 严格递增的函数

Relu：
公式：$g\left(a\right)=ReLu\left(a\right)=\max \left(0,a\right)$

当a小于0时强制转换为0，严格递增的函数 无上限

隐含层的神经网络结构

上面讲的是只有一层直接输出的单层神经网络，下面说一下带有隐含层的神经网络，如图（4）

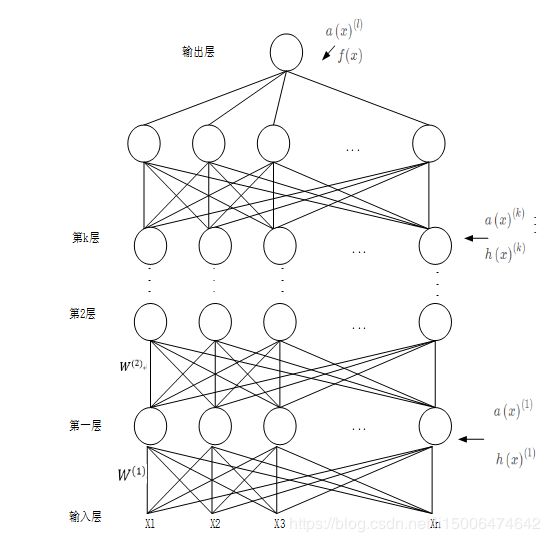
图（4）隐含层的网络结构
每一节点的细节都可以表示成图（5）

$a{\left(x\right)}^{(i)}$表示第$i$层神经元的pre-activation

$a{\left(x\right)}^{(i)}=<a{\left(x_1\right)}^{(i)},a{\left(x_2\right)}^{(i)},a{\left(x_3\right)}^{(i)}...a{\left(x_n\right)}^{(i)}>$

$h{\left(x\right)}^{(i)}$表示第$j$层神经元的post-activation

$h{\left(x\right)}^{(i)}=<h{\left(x_1\right)}^{(i)},h{\left(x_2\right)}^{(i)},h{\left(x_3\right)}^{(i)}...h{\left(x_n\right)}^{(i)}>$

$W^{(i)}$表示第$j$层神经元的权重

$W^{(i)}=<w_1^{(i)},w_2^{(i)},w_3^{(i)},w_4^{(i)}...,w_n^{(i)},>$

第一层可以表示成：

$a{\left(x\right)}^{\left(1\right)}=W^{{\left(1\right)}^T}X+b^{(1)}$

$h{\left(x\right)}^{(1)}=g(a{\left(x\right)}^{\left(1\right)})$

由第一层输入到第二层可以表示成：

$a{\left(x\right)}^{\left(2\right)}=W^{{\left(1\right)}^T}h{\left(x\right)}^{(2)}+b^{(2)}$

$h{\left(x\right)}^{(2)}=g(a{\left(x\right)}^{\left(2\right)})$

因此第k层可以表示成：

$a{\left(x\right)}^{\left(k\right)}=W^{k}h(x{)}^{k-1}+b^{(k)}$

$h{\left(x\right)}^{(k)}=g(a{\left(x\right)}^{\left(k\right)})$

输出层的激活函数一般设置为softmax也就是$g\left(x\right)=\sigma (x)$若在第l层输出

$a{\left(x\right)}^{\left(l\right)}=W^{l}h(x{)}^{l-1}+b^{(l)}$

$h{\left(x\right)}^{(l)}=g(a{\left(x\right)}^{\left(l\right)})=\sigma (a{\left(x\right)}^{\left(l\right)})$

通常为了区分最后一层的激活函数与其他层不同，我们也常常设置$f(x)=h{\left(x\right)}^{(l)}$

根据上面的步骤一直计算，直到最后一层输出$f(x)$也就是完成了神经网络的正向传播

反向传播

假设数据标签为$y$下一步我们要计算$y$与$f(x)$之间的差距，差距越小说明我们的模型越优秀，所以反向传播的目的就是不断减小$y$与$f(x)$之间的差距。所以神经网络的目标函数为公式：
$argmin:\frac{1}{T}{\sum }_{\ast }\phi (f\left(x^{(t)};\theta \right),y^{(t)})+\lambda \Omega \left(\theta \right)$
$\theta$表示神经网络的所以参数：

$\theta =\left\{(W^{(i)},b^{(i)}{)}_{i=1}^{l+1}\right\}$

$f\left(x^{(t)};\theta \right)$表示t时刻参数为$\theta$时模型的输出

$y^{(t)}$表示t时刻的数据集标签

$\lambda \Omega \left(\theta \right)$表示限制参数的正则

$\phi (x,y)$表示损失函数，也就是技术$x和y$的差异，常见的有交叉熵函数

目标函数可以转换成：
$argmax:-\frac{1}{T}{\sum }_{\ast }\phi (f\left(x^{(t)};\theta \right),y^{(t)})-\lambda \Omega \left(\theta \right)$

像这样求目标函数的最大化时，我们最常用的就是随机梯度下降法（SGD）：
第一步：初始化$\theta =\left\{W^{(1)},b^{(1)},...,W^{(l+1)},b^{(l+1)}\right\}$
第二步：循环每个batch： for batch in $(x^t,y^t)$:
循环体内部执行：
1、$\Delta =-\nabla \phi (f\left(x^{(t)};\theta \right),y^{(t)})-\lambda \nabla \Omega \left(\theta \right)$
2、$\theta =\theta +\eta \Delta$
$\eta$:表示步长
这两步也叫做bp算法
也就是说bp算法的核心目的就是求loss（损失函数）对于$\theta$的导数，也就是求解：$\frac{\partial loss}{\partial w^{\left(k\right)}}$和$\frac{\partial loss}{\partial b^{\left(k\right)}}$但是求这两个往往不能直接计算，因此必须依赖它传递的流程，从后往前依次求导，最后才能求出参数$\theta$的导数

所以按照参数传递的顺序，可以分成5个部分：
1、f(x)作为最后一层的输出：$\frac{\partial loss}{\partial f\left(x\right)}$

2、$a{\left(x\right)}^{\left(l\right)}$最后一层的pre-activation：$\frac{\partial loss}{\partial a{\left(x\right)}^{\left(l\right)}}$

3、$h{\left(x\right)}^{\left(k\right)}$：激活后：$\frac{\partial loss}{\partial h{\left(x\right)}^{\left(k\right)}}$

4、$a{\left(x\right)}^{\left(k\right)}$：激活前：$\frac{\partial loss}{\partial a{\left(x\right)}^{\left(k\right)}}$

5、$W^{(k)}和b^{(k)}$参数：$\frac{\partial loss}{\partial w^{\left(k\right)}}$和$\frac{\partial loss}{\partial b^{\left(k\right)}}$

交叉熵

在计算梯度之前先来理解一下损失函数，常用的就是交叉熵

举个例子：
多分类问题：让神经网络判断输入的文本属于哪一类（共四类）

假设模型的输出为：属于第一类的概率为$f(x{)}_1=0.5$,属于第二类的概率为$f(x{)}_2=0.3，$属于第三类的概率为$f(x{)}_3=0.1$，属于第四类的概率为$f(x{)}_4=0.1$，写成向量的形式就是$\left[\begin{array}{c}(0.5)\\ \left(0.3\right)\\ \left(0.1\right)\\ \left(0.1\right)\end{array}\right]$，假如标签$y=2$对应成one-hot编码：$\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]$，则由交叉熵计算出的loss等于：

$loss=(0\times \log 0.5+1\times \log 0.3+0\times \log 0.1+0\times \log 0.1)=-\log 0.3$

因此交叉熵的损失函数为：
$\phi (f(x{)}^{(i)},y^{(i)})=-{\sum }_{c}I(y=c)\cdot \log f(x{)}_c=-\log f(x{)}_y$

$I_{(y=c)}=\{\begin{array}{l}1y=c\\ 0y\ne c\end{array}$

BP算法推导

计算输出层的激活函数的梯度

1、根据BP算法的核心思想首先计算输出层第c个神经元也就是$f{\left(x\right)}_c$的梯度的梯度：$\frac{\partial loss}{\partial f{\left(x\right)}_c}$

$\frac{\partial loss}{\partial f{\left(x\right)}_c}=\frac{\partial -\log f(x{)}_y}{\partial f{\left(x\right)}_c}=-\frac{1}{f{\left(x\right)}_y}\cdot \frac{\partial f{\left(x\right)}_y}{\partial f{\left(x\right)}_c}=-\frac{1}{f{\left(x\right)}_y}\cdot I(y=c)$

2、既然计算出输出层第c个神经元的梯度，下面计算整个输出层的梯度
$\frac{\partial loss}{\partial f\left(x\right)}=-\frac{1}{f{\left(x\right)}_y}\cdot \left[\begin{array}{c}I(y=1)\\ I(y=2)\\ I(y=3)\\ ...\\ I(y=k)\end{array}\right]=-\frac{e(y)}{f{\left(x\right)}_y}$

用这里只是用$e(y)$来表示$\left[\begin{array}{c}I(y=1)\\ I(y=2)\\ I(y=3)\\ ...\\ I(y=k)\end{array}\right]$

计算输出层的pre-activation的梯度

主要是用来计算$a{\left(x\right)}^{\left(l\right)}$最后一层的-activation：$\frac{\partial loss}{\partial a{\left(x\right)}^{\left(l\right)}}$
首先来计算第c神经元的向量$a{\left(x\right)}_c^{\left(l\right)}$:

$\frac{\partial loss}{\partial a{\left(x\right)}_c^{\left(l\right)}}=\frac{\partial -\log f(x{)}_y}{\partial a{\left(x\right)}_c^{\left(l\right)}}=-\frac{1}{f{\left(x\right)}_y}\cdot \frac{\partial f{\left(x\right)}_y}{\partial a{\left(x\right)}_c^{\left(l\right)}}=-\frac{1}{f{\left(x\right)}_y}\cdot \frac{\partial }{\partial a{\left(x\right)}_c^{\left(l\right)}}\cdot \frac{e^{\left(a{\left(x\right)}_y^{\left(l\right)}\right)}}{{\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}}$

$=-\frac{1}{f{\left(x\right)}_y}$$\cdot (\frac{\frac{\partial e^{\left(a{\left(x\right)}_y^{\left(l\right)}\right)}}{\partial a{\left(x\right)}_c^{\left(l\right)}}}{{\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}}-\frac{e^{\left(a{\left(x\right)}_y^{\left(l\right)}\right)}\cdot \frac{\partial {\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}}{\partial a{\left(x\right)}_c^{\left(l\right)}}}{({\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}{)}^2})$

$=-\frac{1}{f{\left(x\right)}_y}\cdot$ $(\frac{e^{\left(a{\left(x\right)}_y^{\left(l\right)}\right)\cdot I_{(y=c)}}}{{\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}}-\frac{e^{\left(a{\left(x\right)}_y^{\left(l\right)}\right)}\cdot e^{\left(a{\left(x\right)}_c^{\left(l\right)}\right)}}{{\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}\cdot {\sum }_{c^{\cdot }}{e}^{\left(a{\left(x\right)}_{c^{\cdot }}^{\left(l\right)}\right)}})$

$=-\frac{1}{f{\left(x\right)}_y}$$\cdot$$(softmax(\left(a{\left(x\right)}_y^{\left(l\right)}\right))\cdot I_{(y=c)}-softmax(\left(a{\left(x\right)}_y^{\left(l\right)}\right))\cdot softmax(\left(a{\left(x\right)}_c^{\left(l\right)}\right)))$

$=-\frac{1}{f{\left(x\right)}_y}(f{\left(x\right)}_y\cdot I_{(y=c)}-f{\left(x\right)}_y\cdot f{\left(x\right)}_c)$ $=-(I_{(y=c)}-f{\left(x\right)}_c)=f{\left(x\right)}_c-I_{(y=c)}$

最后计算出:$\frac{\partial loss}{\partial a{\left(x\right)}_c^{\left(l\right)}}=f{\left(x\right)}_c-I_{(y=c)}$

这只是计算输出层第c个神经元的pre-activation，那么计算输出层的pre-activation就是 (参考第一步)：$\frac{\partial loss}{\partial a{\left(x\right)}^{\left(l\right)}}=f\left(x\right)-e(y)$

计算隐藏层的post-activation的梯度

计算每层 的post-activation，也就是计算$h{\left(x\right)}^{\left(k\right)}$：$\frac{\partial loss}{\partial h{\left(x\right)}^{\left(k\right)}}$

还是先计算第c个神经元的post-activation：$\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}$

直接求$\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}$比较难求，我们来做一个转换也叫梯度的链式求解法则：

所以我们采用链式求解法则进行计算：

$\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}=$ ${\sum }_i\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k+1\right)}}\cdot \frac{\partial a{\left(x\right)}_i^{\left(k+1\right)}}{\partial h{\left(x\right)}_c^{\left(k\right)}}$ $=$ ${\sum }_i\frac{\partial -\log f(x{)}_y}{\partial a{\left(x\right)}_i^{\left(k+1\right)}}\cdot \frac{\partial {\sum }_j{W}_{ij}^{\left(k+1\right)}\cdot h{\left(x\right)}_j^{(k)}}{\partial h{\left(x\right)}_c^{\left(k\right)}}$

=${\sum }_i\frac{\partial -\log f(x{)}_y}{\partial a{\left(x\right)}_i^{\left(k+1\right)}}\cdot W_{ij}^{\left(k+1\right)}=(W_{.j}^{\left(k+1\right)}{)}^T\cdot \frac{\partial -\log f(x{)}_y}{\partial a{\left(x\right)}^{\left(k+1\right)}}$

对于k层的所有神经元的梯度计算：

$\frac{\partial loss}{\partial h{\left(x\right)}^{\left(k\right)}}=(W^{\left(k+1\right)}{)}^T\cdot \frac{\partial -\log f(x{)}_y}{\partial a{\left(x\right)}^{\left(k+1\right)}}$

计算隐藏层的pre-activation的梯度

同理，我们先计算第k层第c个神经元的pre-activation：$\frac{\partial loss}{\partial a{\left(x\right)}_c^{\left(k\right)}}$

$\frac{\partial loss}{\partial a{\left(x\right)}_c^{\left(k\right)}}$=$\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}\cdot \frac{\partial h{\left(x\right)}_c^{\left(k\right)}}{\partial a{\left(x\right)}_c^{\left(k\right)}}=\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}\cdot g^{{}^{\prime }}(a(x{)}_c^{(k)})$

对于k层所有神经元post-activation计算：

$\frac{\partial loss}{\partial a{\left(x\right)}^{\left(k\right)}}=\frac{\partial loss}{\partial h{\left(x\right)}_c^{\left(k\right)}}\odot g^{{}^{\prime }}(a(x{)}^{(k)})$

计算参数$w和b$的梯度

先计算k层第i个神经元对应的第j个权重$w_{ij}^{(k)}$: $\frac{\partial loss}{\partial w_{ij}^{\left(k\right)}}$

$\frac{\partial loss}{\partial w_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}\cdot \frac{\partial a{\left(x\right)}_i^{\left(k\right)}}{\partial w_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}\cdot \frac{\partial {\sum }_j{W}_{ij}^{\left(k\right)}\cdot h{\left(x\right)}_j^{(k-1)}+b_{ij}^{(k)}}{\partial w_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}\cdot h{\left(x\right)}_j^{(k-1)}$

对于k层所有的权重$w^{(k)}$:

$\frac{\partial loss}{\partial w^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}^{\left(k\right)}}\cdot (h{\left(x\right)}^{(k-1)}{)}^T$

再计算k层第i个神经元对应的第j个偏置$b_{ij}^{(k)}$: $\frac{\partial loss}{\partial b_{ij}^{\left(k\right)}}$

$\frac{\partial loss}{\partial b_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}\cdot \frac{\partial a{\left(x\right)}_i^{\left(k\right)}}{\partial b_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}\cdot \frac{\partial {\sum }_j{W}_{ij}^{\left(k\right)}\cdot h{\left(x\right)}_j^{(k-1)}+b_{ij}^{(k)}}{\partial b_{ij}^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}_i^{\left(k\right)}}$

对于k层所有的权重$b^{(k)}$:

$\frac{\partial loss}{\partial b^{\left(k\right)}}=\frac{\partial loss}{\partial a{\left(x\right)}^{\left(k\right)}}$

BP算法总结

根据上面有一点点小复杂的计算我们可以知道：

输出层的梯度：

$\nabla f(x)=-\frac{e(y)}{f{\left(x\right)}_y}$

$\nabla a(x{)}^{(l)}=f\left(x\right)-e(y)$

隐藏层的梯度：

$\nabla h(x{)}^{(k)}=(W^{\left(k+1\right)}{)}^T\cdot \nabla a(x{)}^{(k+1)}$

$\nabla a(x{)}^{(k)}=\nabla h(x{)}^{(k)}\odot g^{{}^{\prime }}(a(x{)}^{(k)})$

参数的梯度：
$\nabla w^{(k)}=\nabla a(x{)}^{(k)}\cdot (h{\left(x\right)}^{(k-1)}{)}^T$

$\nabla b^{(k)}=\nabla a(x{)}^{(k)}$

总结
所以神经网络计算大约有3步：
1、前向计算
2、反向传播计算梯度
3、更新参数

到此一个基本神经网络的就了解的差不多了下面，再聊一下RNN吧

循环神经网络（RNN）

在我们的生活中是有很多的时序性的数据，比如：语音，天气，股票，文本都是随时间的 变化而变化的，为了处理这样的数据，设计了一种循环神经网络也叫递归神经网络RNN如图（6）

如图（6）所示t=1时刻时我们输入数据$x_1$，和神经网络一样先进行线性的转化pre-activation在进行非线性的转化post-activation ：

当$t=1$时：
$h_1=f(w_{x1}\cdot x_1+w_{h1}\cdot h_0+b_{t1})$

$f(x)$表示激活函数，$h_0$一般设置为0 ，$b_{t1}$表示偏置

$y_1=g(w_{y1}\cdot h_1+b_{i1})$

$g(x)$表示激活函数，$b_{i1}$表示输出层的偏置

当$t=2$时：
$h_2=f(w_{x2}\cdot x_2+w_{h2}\cdot h_1+b_{t2})$

$f(x)$表示激活函数 ，$b_{t2}$表示偏置

$y_2=g(w_{y2}\cdot h_2+b_{i2})$

当$t=n$时：

$h_n=f(w_{xn}\cdot x_n+w_{hn}\cdot h_{(n-1)}+b_{tn})$

$y_n=g(w_{yn}\cdot h_n+b_{in})$

从公式中我们可以看出当时间到了$n$时$h_n$不仅包含了当前数据信息，还包含了前面数据的信息，那对应输出的$y_n$也是包含整个文本信息的输出，假设n为最后一层，我们常常用$y_n$来表示句子信息和段落信息用来处理我们的下游任务。
而且每一层都会有损失函数的计算，所有损失函数是: $loss={\sum }_i^{n}los{s}_i$

可以看出rnn是随着时间的增加，层数也在不断的增加，因此，rnn是在时间维度上的Deep Model

梯度消失和梯度爆炸的问题

为什么会出现梯度消失和梯度爆炸的问题呢？我们用数学公式来进行说明：

在rnn中假设我们计算$t=4$时刻的对$h_1$的梯度，也就$los{s}_4$时的梯度：$\frac{\partial l_4}{\partial h_1}$

一般情况下我们无法直接计算$\frac{\partial l_4}{\partial h_1}$，因此使用链式求导法则来进行计算 :

$\frac{\partial l_4}{\partial h_1}=\frac{\partial l_4}{\partial h_2}\cdot \frac{\partial h_2}{\partial h_1}=\frac{\partial l_4}{\partial h_3}\cdot \frac{\partial h_3}{\partial h_2}\cdot \frac{\partial h_2}{\partial h_1}=\frac{\partial l_4}{\partial h_4}\cdot \frac{\partial h_4}{\partial h_3}\cdot \frac{\partial h_3}{\partial h_2}\cdot \frac{\partial h_2}{\partial h_1}$

将计算过程扩展一下为：

$\frac{\partial l_i}{\partial h_j}=\frac{\partial l_i}{\partial h_i}\cdot {\prod }_{j\le t\le i}\frac{\partial h_t}{\partial h_{t-1}}$

若激活函数用sigmold则：
$h_t=\sigma (w_{xt}\cdot x_t+w_{ht}\cdot h_{(t-1)}+b_{tt})$

$\frac{\partial h_t}{\partial h_{t-1}}=diag({\sigma }^{、}(w_{xt}\cdot x_t+w_{ht}\cdot h_{(t-1)}+b_{tt}))\cdot w_{ht}$

$diag$：指的是对矩阵的处理，因为$h_t$和$h_{t-1}$是向量的形式，因此求导的结果是矩阵。因此:

$\frac{\partial l_i}{\partial h_j}=\frac{\partial l_i}{\partial h_i}\cdot {\prod }_{j\le t\le i}diag({\sigma }^{、}(w_{xt}\cdot x_t+w_{ht}\cdot h_{(t-1)}+b_{tt}))\cdot w_{ht}$

根据公式我们可以看出，当$j>i$很多时，计算$\frac{\partial l_i}{\partial h_j}$我们需要乘以很多很多的项，如果这些项都小于0的话，那在计算梯度时会越乘越小，有可能导致梯度很小导致梯度消失，如果这些项都大于0的话就会越乘越大，就有可能导致梯度爆炸。

LSTM和GRU

由上面我们知道，rnn有可能造成梯度消失的问题（爆炸的问题比较好解决就不细说了）这样就会带来特征提取的不够长，因此我们又发明了LSTM和GRU

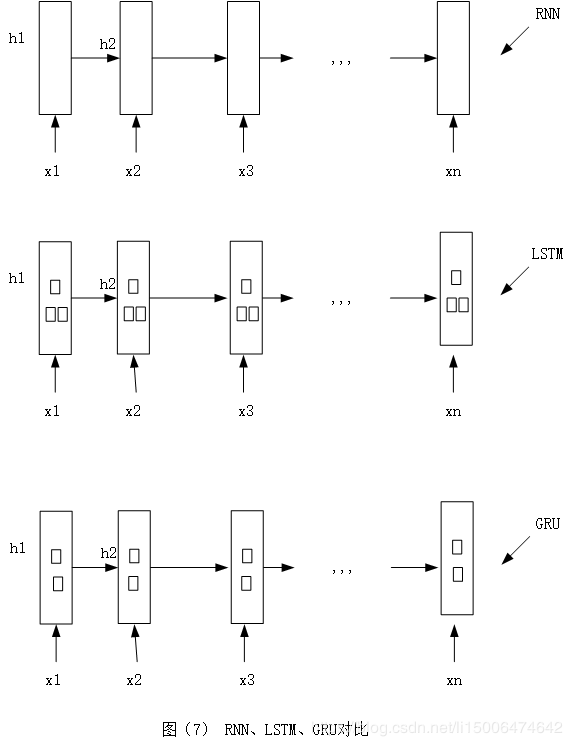
从图（7）我们可以看出RNN和LSTM还有GRU外形其实是差不多，只是LSTM和GRU比RNN多了几个门，也就是多了几个操作，我们先看一下

LSTM在神经元内部的操作

：

$f^{(t)}=\sigma (u_f\cdot x_t+w_f\cdot h_{t-1}+b_f)$ \qquad (1) \qquad $(u_f,w_f,b_f)$

$i^{(t)}=\sigma (u_i\cdot x_t+w_i\cdot h_{t-1}+b_i)$ \qquad (2) \qquad $(u_i,w_i,b_i)$

$o^{(t)}=\sigma (u_o\cdot x_t+w_o\cdot h_{t-1}+b_o)$ \qquad (3) \qquad $(u_o,w_o,b_o)$

$\overline{c^{(t)}}=tanh(u_c\cdot x_t+w_c\cdot h_{t-1}+b_c)$ \qquad (4) \qquad $(u_c,w_c,b_c)$

$c^{(t)}=f^{(t)}\odot c^{(t-1)}+i^{(t)}\odot \overline{c^{(t)}}$ \qquad (5)

$h^{(t)}=o^{(t)}\odot tanh(c^{(t)})$ \qquad (6)

从式(5)中可以看出$f^{(t)}$是用来决定上一层获取的信息量$f^{(t)}$=1就是指全部获取$f^{(t)}$=0就是指遗忘上一层所有信息。$\overline{c^{(t)}}$表示获取额外信息量，$i^{(t)}$表示决定获取$\overline{c^{(t)}}$的大小

可以看出$h^{(t)}$计算时有选择性的记忆上次信息和获取当前信息。

GRU

$u^{(t)}=\sigma (u_u\cdot x_t+w_u\cdot h_{t-1}+b_u)$ \qquad (1) \qquad $(u_u,w_u,b_u)$

$r^{(t)}=\sigma (u_r\cdot x_t+w_r\cdot h_{t-1}+b_r)$ \qquad (2) \qquad $(u_r,w_r,b_r)$

$\overline{h^{(t)}}=tanh(w_h\cdot (u_h\cdot x_t+r^{(t)}\cdot h_{t-1}+b_h))$ \qquad (3) \qquad $(u_h,w_h,b_h)$

$h^{(t)}=(1-u^{(t)})\cdot h^{(t-1)}+u^{(t)}\cdot \overline{h^{(t)}}$ \qquad (4)

从（4）中我们可以看到$h^{(t-1)}$表示旧的信息，$\overline{h^{(t)}}$表示新的信息，而$u^{(t)}$是做的加权平均的操作，也就是有百分之多少记忆旧的信息，有百分之多少获取新的信息。参数和运算要比LSTM少很多，速度也相对快一些

结束

好了神经网络的知识就介绍到这里，博主肝了两天，码字不易，还请各位转载标明出处，当然有什么不懂的或者是我错误的地方，及时留言哦，欢迎大家交流！！