数论 + 概率论 - Paperfolding - HDU 6822
数论 + 概率论 - Paperfolding - HDU 6822
2020 Multi-University Training Contest 5
题意:
对 一 张 纸 进 行 n 次 操 作 , 对一张纸进行n次操作, 对一张纸进行n次操作,
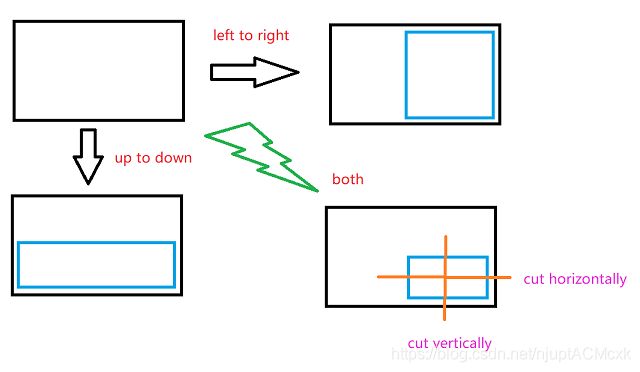
每 次 操 作 允 许 横 向 对 折 或 者 竖 向 对 折 , 两 种 操 作 都 是 等 概 率 的 , 每次操作允许横向对折或者竖向对折,两种操作都是等概率的, 每次操作允许横向对折或者竖向对折,两种操作都是等概率的,
最 后 将 纸 片 横 向 平 分 剪 一 刀 , 竖 向 平 分 剪 一 刀 , 最后将纸片横向平分剪一刀,竖向平分剪一刀, 最后将纸片横向平分剪一刀,竖向平分剪一刀,
对 最 后 分 成 的 纸 片 数 量 计 算 数 学 期 望 。 答 案 对 998244353 取 模 。 对最后分成的纸片数量计算数学期望。答案对 998244353取模。 对最后分成的纸片数量计算数学期望。答案对998244353取模。
输入:
T 组 测 试 数 据 , T组测试数据, T组测试数据,
每 组 包 括 一 个 正 整 数 n 。 每组包括一个正整数n。 每组包括一个正整数n。
输出:
一 个 正 整 数 , 表 示 答 案 。 一个正整数,表示答案。 一个正整数,表示答案。
Sample Input
2
0
1
Sample Output
4
6
数据范围:
1 ≤ T ≤ 1 0 5 , 0 ≤ n ≤ 1 0 18 1≤T≤10^5,0≤n≤10^{18} 1≤T≤105,0≤n≤1018
分析:
设 n 次 操 作 中 , 有 i 次 横 向 对 折 的 操 作 , 设n次操作中,有i次横向对折的操作, 设n次操作中,有i次横向对折的操作,
则 最 终 能 够 将 纸 片 分 成 ( 2 i + 1 ) ( 2 n − i + 1 ) 块 。 则最终能够将纸片分成(2^i+1)(2^{n-i}+1)块。 则最终能够将纸片分成(2i+1)(2n−i+1)块。
记 X i 为 事 件 : 纸 被 横 向 对 折 i 次 后 , 最 终 被 分 成 的 小 纸 片 的 数 量 。 记X_i为事件:纸被横向对折i次后,最终被分成的小纸片的数量。 记Xi为事件:纸被横向对折i次后,最终被分成的小纸片的数量。
则 P ( X i ) = C n i ⋅ 1 2 n , 即 事 件 X i 发 生 的 概 率 。 则P(X_i)=C_n^i·\frac{1}{2^n},即事件X_i发生的概率。 则P(Xi)=Cni⋅2n1,即事件Xi发生的概率。
数 学 期 望 数学期望 数学期望
E ( X ) = ∑ i = 0 n P ( X i ) ⋅ X i = 1 2 n ∑ i = 0 n C n i × ( 2 i + 1 ) ( 2 n − i + 1 ) = 1 2 n ∑ i = 0 n C n i ( 2 n + 2 i + 2 n − i + 1 ) E(X)=\sum_{i=0}^nP(X_i)·X_i=\frac{1}{2^n}\sum_{i=0}^nC_n^i×(2^i+1)(2^{n-i}+1)=\frac{1}{2^n}\sum_{i=0}^nC_n^i(2^n+2^i+2^{n-i}+1) E(X)=i=0∑nP(Xi)⋅Xi=2n1i=0∑nCni×(2i+1)(2n−i+1)=2n1i=0∑nCni(2n+2i+2n−i+1)
根 据 二 项 式 定 理 : 根据二项式定理: 根据二项式定理:
∑ i = 0 n C n i x i = ∑ i = 0 n C n i x i ⋅ 1 n − i = ( 1 + x ) n \sum_{i=0}^nC_n^ix^i=\sum_{i=0}^nC_n^ix^i·1^{n-i}=(1+x)^n i=0∑nCnixi=i=0∑nCnixi⋅1n−i=(1+x)n
故 : ∑ i = 0 n C n i 2 i = 3 n , ∑ i = 0 n C n i 2 − i = ( 1 + 1 2 ) n 故:\sum_{i=0}^nC_n^i2^i=3^n,\sum_{i=0}^nC_n^i2^{-i}=(1+\frac{1}{2})^n 故:∑i=0nCni2i=3n,∑i=0nCni2−i=(1+21)n
最 终 答 案 : 最终答案: 最终答案:
1 2 n ∑ i = 0 n C n i ( 2 n + 2 i + 2 n − i + 1 ) = 1 2 n ( 4 n + 3 n + 2 n ( 1 + 1 2 ) n + 2 n ) \frac{1}{2^n}\sum_{i=0}^nC_n^i(2^n+2^i+2^{n-i}+1)=\frac{1}{2^n}(4^n+3^n+2^n(1+\frac{1}{2})^n+2^n) 2n1i=0∑nCni(2n+2i+2n−i+1)=2n1(4n+3n+2n(1+21)n+2n)
代码:
#include