论文笔记：Neural Graph Collaborative Filtering

前言

论文链接：https://arxiv.org/abs/1905.08108
github：https://github.com/talkingwallace/NGCF-pytorch
参考：https://www.jianshu.com/p/16c8973ef8ff
https://zhuanlan.zhihu.com/p/110682271
https://blog.csdn.net/weixin_37913042/article/details/99712729

CF方法：

• 协同过滤学习模型从项目的丰富侧面信息中学习的深层表示来扩展MF嵌入功能；
• 神经协同过滤模型用非线性神经网络取代内积的MF交互函数。

在 user-item interaction graph 上使用 GNN 来学习 user 向量和item 向量，用户向量和项向量的内积来预测评分。从user向量和item的向量表示出发进行学习，将学习结果做内积得到预测评分来完成推荐系统中的评分预测任务。相较于GC-MC方法从评分矩阵出发将评分预测问题转换为矩阵补全的连接预测的问题，两者具有一定的区别

学习 users 和 items 的向量表示是现代推荐系统的核心。从早期的矩阵分解到最近出现的基于深度学习的方法，现有的工作通常通过从描述用户(或项目)的现有特性(如ID和属性)映射来获得用户(或项目)的嵌入。这种方法的一个固有缺点是，隐藏在用户-项目交互中的协作信号没有在嵌入过程中编码。因此，由此产生的嵌入可能不足以捕获协作过滤效果。更具体地来说，传统的方法主要是对ID或者属性进行编码得到embedding，再基于user-item interaction定义重构损失函数并进行解码。可以看出，user-item interaction只用到了解码端，而没有用到编码端。这样会导致，学习到的embedding的信息量不够，为了更好的预测，只能依赖于复杂的interaction (decoder) function来弥补次优的embedding在预测上的不足。

虽然直接地使用交互功能能弥补次优嵌入的不足，但是在实际开发中，交互的规模可以容易地达到数百万甚至更大，使得难以提取期望的协作信号。在这项工作中，将用户-项目交互更具体地集成到嵌入过程中二部图结构。提出了一种新的推荐框架神经图协同过滤算法(NGCF)，该算法利用用户项图的结构，在用户项图上传播嵌入。这就导致了用户项图中高阶连通性的表达建模，有效地将协作信号显式地注入到嵌入过程中。

1. 高阶连通性的概念

左边所示的为协同过滤用户-项目交互的基本交互图，双圆圈表示需要预测的用户$u_1$，右图为左图以用户$u_1$为根节点扩展的树形结构，$l$为到达用户$u_1$的路径长度（可以作为兴趣重要度的权重值）
从右图中可以看到，同路径长度为3的项目$i_4$、$i_5$中，明显用户对$i_4$的兴趣度高于$i_5$，这是因为$<i_4,u_1>$连接的路径有两条，分别为$i_4$->$u_2$->$i_2$->$u_1$、$i_4$->$u_3$->$i_3$->$u_1$，而$<i_5,u_1>$则只有一条，为$i_5$->$u_2$->$i_2$->$u_1$。所以通过这些树形结构来查看$u_1$对项目的兴趣，看项目与用户的连通性。这就是高阶连通性的概念。

1.1 高阶连通性嵌入层建立

在实际的工作中提出了嵌入函数中高阶连通性信息的建模方法.而不是将交互图扩展为一棵复杂的树。
本章论文设计了一种在图上递归传播的神经网络方法，受最近发展的图神经网络的启发，可以看作是在嵌入空间中构造信息流。
通过在神经网络中，插入一个嵌入传播层，它通过聚合交互项(或用户)的嵌入来细化用户(或项)的嵌入。叠加多重嵌入传播层，我们可以强制嵌入，以捕获协作信号的高阶连通性.
以Figure1为例，堆叠两层捕获$u_1$←$i_2$←$u_2$的行为相似性，堆叠三层捕获$u_1$←$i_2$←$u_2$←$i_4$和潜在的信息流的强度(由层间的大小估计权重值)确定$i_4$和$i_5$的推荐优先级。

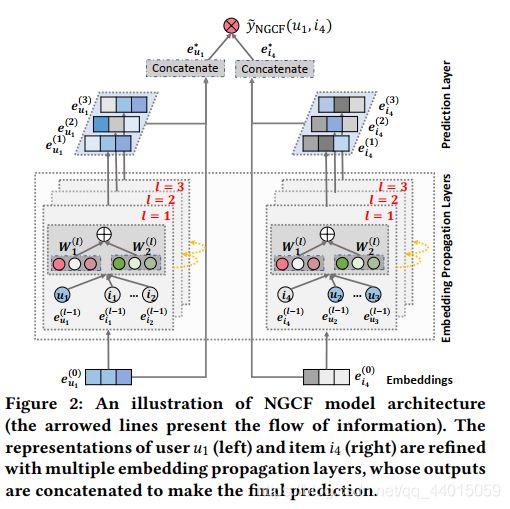
2. NGCF模型

整体上来看该模型由三部分结构组成：

1. Embedding Layer–提供用户嵌入和物品嵌入初始化;
2. Embedding Propagation Layer(Message Construction，Message Aggregation)–多嵌入传播层：通过注入高阶连通性关系来细化嵌入;
3. Prediction Layer–预测层：整合来自不同传播层的细化嵌入，输出用户-项目对的亲和度得分。

2.1 Embedding Layer

嵌入层，offers and initialization of user embeddings and item embeddings
$$E=[e_{u1,...,e_{uN},e_{i1},...,e_{iM}}]\text{\hspace{1em}(1)}$$

传统的方法直接将$E$输入到交互层，进而输出预测值。而NGCF将$E$输入到多层嵌入传播层，通过在二部图上进行嵌入的传播来对嵌入进行精炼。

2.2 Embedding Propagation Layer

多层嵌入传播层，refine the embeddings by injecting high-order connectivity relations

包括两个步骤，Message construction和Message aggregation。这个部分和KDD2018的GCMC是类似的描述方式。

2.2.1 Message Construction

对于每个user-item pair $(u,i)$, 定义从$i$到$u$传递的message如下：
$$m_{u<-i}=f(e_i,e_u,p_{ui})\text{\hspace{1em}(2)}$$
其中,$m_{u<-i}$定义为message embedding。$f(\cdot )$是message encoding function，将user和item的 embedding $e_u,e_i$作为输入,并使用$p_{ui}$来控制每条边edge $(u,i)$在每次传播中的衰减系数。

具体的，作者使用如下message encoding function:
$$m_{u<-i}=\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}(W_1{e}_i+W_2(e_i\odot e_u))\text{\hspace{1em}(3)}$$
可以看出作者不仅考虑了message的来源 $e_i$（传统图卷积方法只考虑这个），还考虑了信息来源和信息目的地之间的关系，即$e_i\odot e_u$，这个element-wise product是典型的特征交互的一种方式，值得学习。 $p_{ui}=\frac{1}{\sqrt{|{\mathcal{N}}_u||{\mathcal{N}}_i|}}$, ${\mathcal{N}}_u$是用户 $u$ 的1-hop neighbors。从表示学习角度： $p_{ui}$ 反映了历史交互item对用户偏好的贡献程度。从信息传递角度，$p_{ui}$ 可以看做是折扣系数，随着传播路径长度的增大，信息慢慢衰减（这个可以通过叠加多层，并代入到式子，会发现前面系数也是连乘在一起了，说明路径越长，衰减越大）。

2.2.2 Message Aggregation

这个阶段，我们将从用户 $u$ 的邻居传递过来的信息进行汇聚来提炼用户 $u$ 的嵌入表示。
$$e_u^{(1)}=LeakyReLU(m_{u<-u}+\sum _{i\in {\mathcal{N}}_u}{m}_{u<-i})\text{\hspace{1em}(4)}$$

$e_u^{(1)}$ 是经过一层嵌入传播层得到的提炼后的用户 $u$ 嵌入表示。$LeakyReLU$允许对于正反馈信息和少部分负反馈信息的编码。
$m_{u<-u}=W_1{e}_u$考虑了self-connection。此处的$W_1$与上面的消息传递公式中的$W_1$权值共享。

item的嵌入表示同理可得。embedding propagation layer的好处在于显示地挖掘 first-order connectivity信息来联系user和item的表示。

得到的 $e_u^{(1)}$ 可以作为下一个embedding propagation layer的输入，通过叠加多层，可以挖掘multi-hop的关联关系。迭代式如下：
$$e_u^{(l)}=LeakyReLU(m_{u<-u}^{(l)}+\sum _{i\in {\mathcal{N}}_u}{m}_{u<-i}^{(l)})\text{\hspace{1em}(5)}$$
其中，
$$m_{u<-i}^{(l)}=p_{ui}(W_1^{(l)}{e}_i^{(l-1)}+W_2^{(l)}(e_i^{(l-1)}\odot e_u^{(l-1)}))\text{\hspace{1em}(6)}$$
$$m_{u<-u}^{(l)}=W_1^l{e}_u^{(l-1)}\text{\hspace{1em}(7)}$$

进一步，作者给出了上述Equation(5), (6) 过程的矩阵表示形式，有助于实现layer-wise propagation。
$$\underset{{\mathbb{R}}^{(N+M)\times d_l}}{E^{(l)}}=LeakyReLU(\underset{{\mathbb{R}}^{(N+M)\times (N+M)}}{(\mathcal{L}+I)}\stackrel{{\mathbb{R}}^{(N+M)\times d_{l-1}}}{E^{l-1}}\underset{{\mathbb{R}}^{d_{l-1}\times d_l}}{W_1^{(l)}}+\stackrel{{\mathbb{R}}^{(N+M)\times (N+M)}}{\mathcal{L}}\underset{(N+M)\times d_{l-1}}{E^{(l-1)}}\odot \stackrel{(N+M)\times d_{l-1}}{E^{(l-1)}}\underset{{\mathbb{R}}^{d_{l-1}\times d_l}}{W_2^{(l)}})\text{\hspace{1em}(8)}$$

其中， $E^{(l)}\in {\mathbb{R}}^{(N+M)\times d_l}$ ，即：把user, item的embeddings矩阵concat在一起，一起进行传播。也就是说，上述是user，item共同进行传播的表示形式，因此所有的矩阵都是concat在一起的形式。

作者说，$\mathcal{L}$ 表示user-item interaction graph的拉普拉斯矩阵，$\mathcal{L}=D^{-1/2}A{D}^{-1/2}$ ，其中，$A\in {\mathbb{R}}^{(N+M)\times (N+M)}$是邻接矩阵，是user-item 交互矩阵和item-user交互矩阵构成的，即：$$A=\left[\begin{array}{cc}0& R\\ R^T& 0\end{array}\right]$$
对于上述的矩阵表示，前一项代表了关于$W_1$四个式子得集合(由于矩阵是concat的形式，综合考虑user->item和item->user)，关于单位矩阵$I$意味着self-connection的两项，关于$\mathcal{L}$作者在文中表示相当于$p_{ui}$。因此可以一一对应起来了，一目了然。

2.3 Prediction Layer

预测层，aggregates the refined embeddings from different propagation layers and outputs the affinity score of a user-item pair.

最终的嵌入表示是原始的embedding和所有嵌入传播层得到的embedding全部concat在一起的结果。即：
$$e_u^{\ast }=concat(e_u^{(0)},e_u^{(1)},...,e_u^L)\text{\hspace{1em}(9)}$$

$e_u^{(0)}$ 是初始化的embeddings。 $e_i^{\ast }$ 同理可得。

最后预测user-item交互的时候使用点乘：

$${\hat{y}}_{NGCF}(u,i)={e_u^{\ast }}^T{e}_i^{\ast }\text{\hspace{1em}(10)}$$

最后作者采用的是pairwise BPR loss进行优化。

$$Loss=-\sum _{(u,i,j)\in O}ln\sigma ({\hat{y}}_{ui}-{\hat{y}}_{uj}+\lambda ||\Theta |{|}_2^2)\text{\hspace{1em}(10)}$$
其中$O=\{(u,i,j)|(u,i)\in R^{+},(u,j)\in R^{-}\}$，$R^{+}$是观测数据，$R^{-}$是未观测数据，$\Theta =\{E,\{W_1^{(l)},W_2^{(l)}{\}}_{l=1}^L\}$是所有的可训练参数。

3. 实验

3.1 评价指标

在三个真实的数据集上进行实验来评价RGCF提出的方法，特别是嵌入传播层。本文的目标是回答以下研究问题：

RQ 1：NGCF与目前最先进的CF方法相比表现如何？·
RQ 2：不同的超参数设置(例如，层的深度、嵌入传播层、层聚集机制，消息丢弃和结点丢弃)影响NGCF？
RQ3：表示如何从高阶连通性中受益？

三个数据集Gowalla、Yelp2018和Amazon-book：

• Yelp2018：这个数据集来自2018年版的Yelp挑战。
• Amazon-book：Amazon-Review是广泛使用的产品推荐数据集
• Gowalla：这是从Gowallahere获得的签入数据集，用户通过签入共享他们的位置。
• 
  对于测试集中的每个用户，将用户没有交互的所有项作为否定项处理。然后每个方法输出用户的除训练集中使用的正面项目外，其他项目的偏好得分总体上都是如此。为了评估top-k推荐和优选的有效性，我们采用了两种广泛使用的评估方法召回率，和归一化折损累计增益
  以下模型为常用的CF模型，本文利用了NGCF 与一下模型对比，说明NGCF的确优于常用的CF模型，本文也考虑了用SpectralCF 模型加入性能对比当中，但是发现特征分解导致高的时间成本和资源成本，特别是当用户和项目数量很大时性能特别差，但是在小型数据集中性能很好，所以没有选择它作为比较。为了公平的比较，所有的方法都优化了BPR损失（2.3所用的损失函数）。
  结果如下：

3.2 RQ 1 :

可以看到NGCF与目前的推荐模型比较结果，可以看到以下观察结果：

• MF对三个数据集的性能较差。这表明内部嵌入不足以捕获用户和项目之间的复杂关系，从而进一步限制性能。Ne’uMf在所有情况下都优于MF，这说明了用户和项嵌入之间非线性特征交互的重要性
• 与MF和NeuMF相比，GC-MC的性能验证了一阶邻域的加入可以提高表征学习的效果。然而在Yelp2008数据集中，ndcg低于NeuMf,原因可能是GC-MC未能充分探讨用户和项之间的非线性特征交互。
• 在大多数情况下，CMN的性能通常优于GC-MC。这种改善可以归因于神经注意机制，它可以指定每个相邻用户注意力的权重，而不是相同的或启发式权重使用的GC-MC。
• 在Gowalla和AmazonBook中，PinSage略微优于CMN，而Yelp2018年表现更好；同时，HOPRec通常在大多数情况下取得显著的改进，这是有意义的，因为Pinsage在嵌入函数中引入了高阶连通性，并且HOP-rec利用邻居来丰富训练数据，而cmn则考虑了类似的情况。只有用户。因此，它指出了建立高阶连通性或邻居模型的积极作用
• NGCF始终在所有数据集上获得最佳性能，特别是在Gowalla、Yelp2018和Am，这验证了在嵌入函数中使用高阶连通性捕获协同信号的重要性。
  稀疏性问题通常限制推荐系统的表现力，因为不活跃用户的交互不足以生成高质量的表示。我们调查是否利用高阶连通信号有助于缓解此问题。
  为此，我们对不同稀疏程度的用户组进行了实验。特别是，根据用户交互编号，我们将测试集划分为四个组，每个组都是最新的。他的互动也是一样的
  
  NGCF和HOP-Rec在所有用户组上的表现始终优于所有其他基础设施。它证明了利用高阶连通性极大地促进了不活跃的用户模型学习性能，因为协同信号可以有效地被捕获。因此，有希望解决推荐系统中的稀疏问题。

3.3 RQ2:

层数的影响：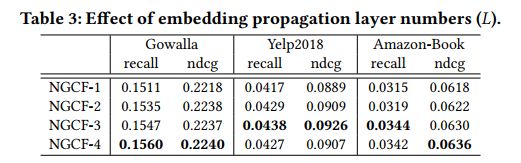
2层和3层的NGCF明显比1层的NGCF性能有所提高，这说明层数的加深对的确对提高NGCF的性能有所帮助，但是当上升到4层的时候，可以NGCF对Gowall数据集的recall和ndcg提升很多，但是其他数据集则相对降低，这说明当NGCF的嵌入传播层设置在4层的时候，NGCF产生了过拟合，所以NGCF嵌入传播层设置在三层的时候，对性能提高最大，并且降低了发生过拟合的风险

层聚集机制:

对嵌入传播层，聚合了一些算法，并对聚合后的算法对比基线，可以看到，聚合算法和传播层的时候，模型的性能不升反降，这说明聚合并不是一个好的想法，但是对比NGCF-1PinSage和SVD++可以知道，非线性变换对图形神经网络的性能提高有一定的帮助。

节点丢弃和消息丢弃技术:
节点丢弃和消息丢弃技术主要是用来防止NGCF产生过拟合，图3.5显示了不消息丢弃的比率p1和节点丢弃率p2，对NGCF产生的影响.如在Gowall数据集中，节点丢弃率p2设置在0.02中，模型达到最高的性能，召回率达到0.151，而在设置p2明显提高召回率比设置消息丢弃率有效得多。这个原因可能是丢弃了特定用户和特定项对模型的鲁棒性有更好的提升，也是节点的影响，因此说明节点丢弃比消息丢弃更有效。

3.4 RQ 3:

解释高阶连通性的影响：
为测试高阶连通性对推荐预测的影响，本文从 Gowalla数据集中随机抽取6个数据 量的数据集，并可视化他们的关系

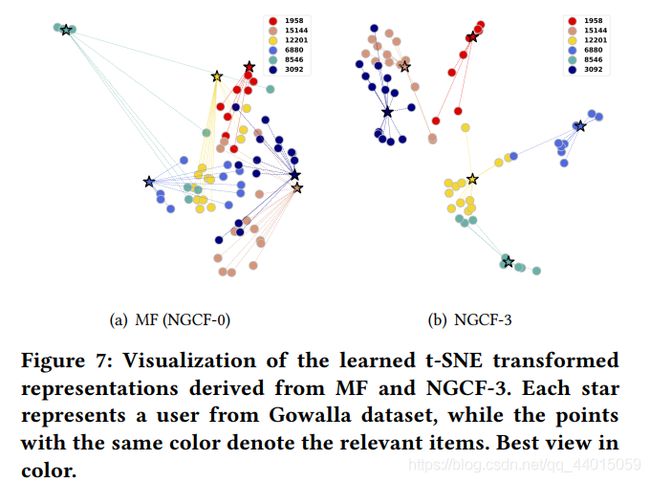
MF与NGCG-3的用户与项目关系性的可视化
从图3.6可以看到NDCG更好地分类了用户与项目的连接性，这意味着具有相同颜色（有相同兴趣的用户与相关的项目）的点倾向于形成簇。
对比a和b，NGCF堆叠到三层嵌入传播层的时候，其历史项目的嵌入往往更接近。这更好地说明三层嵌入传播层能够将显式协作信号(通过NGCF-3)写入到模型表示中。