PyTorch学习笔记-4.PyTorch损失优化

4.PyTorch损失优化

4.1.权值初始化

4.1.1.梯度消失与爆炸

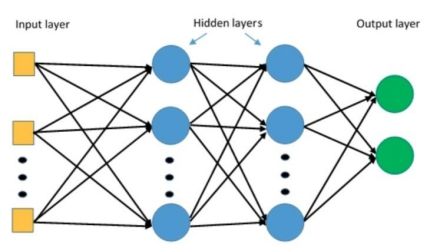
对于一个含有多层隐藏层的神经网络来说，当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。梯度爆炸与之相反。

例如下图的神经网络：

其中，，，

对求导得：

从上式可以看出，损失函数对求导是由多个求导累乘的结果，对于其中的每个求导，如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸。

 

代码实现：

# -*- coding: utf-8 -*-
import torch
import random
import numpy as np
import torch.nn as nn

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(3)  # 设置随机种子

class MLP(nn.Module):
    def __init__(self, neural_num, layers):
        super(MLP, self).__init__()

# 构建layers层，每层neural_num个神经元的神经网络
        self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
        self.neural_num = neural_num

    def forward(self, x):
        for (i, linear) in enumerate(self.linears):
            x = linear(x)

        return x

    def initialize(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                # 参数初始化，对每层的权重初始化为均值为0，标准差为1的正太分布。
                nn.init.normal_(m.weight.data)  

# 层数
layer_nums = 100
# 每层神经元个数
neural_nums = 256
# 批大小
batch_size = 16

# 构建MLP模型
net = MLP(neural_nums, layer_nums)
net.initialize()

inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1

output = net(inputs)
print(output)

tensor([[nan, nan, nan,  ..., nan, nan, nan],         [nan, nan, nan,  ..., nan, nan, nan],         ...,         [nan, nan, nan,  ..., nan, nan, nan],         [nan, nan, nan,  ..., nan, nan, nan]], grad_fn=)

 

可以看到最终输出的全部为nan，可以打印每层的标准差，查看每层的输出情况，以及最终出现nan层的标准差，在MLP类forward方法中，遍历时进行输出

代码实现：

def forward(self, x):
    for (i, linear) in enumerate(self.linears):
        x = linear(x)

        # 打印每层标准差
        print("layer:{}, std:{}".format(i, x.std()))
        if torch.isnan(x.std()):
            # 判断如果当前层的标准差已经是nan，则打印当前层并跳出循环
            print("output is nan in {} layers".format(i))
            break

    return x

layer:0, std:15.959932327270508 layer:1, std:256.6237487792969     ... layer:29, std:1.322983152787379e+36 layer:30, std:2.0786820453988485e+37 layer:31, std:nan output is nan in 31 layers tensor([[        inf, -2.6817e+38,         inf,  ...,         inf,                  inf,         inf],         [       -inf,        -inf,  1.4387e+38,  ..., -1.3409e+38,          -1.9659e+38,        -inf],         ...,         [        inf,         inf,        -inf,  ...,        -inf,                  inf,  1.7432e+38]], grad_fn=)

 

可以看到上面在第31层时，输出以及很大或者很小，为何会出现这样的问题？

首先，对于方差有

若E(X)=0  ，则

又对于第一层隐藏层的第一个元素：

则这个元素对应的方差为：

标准差则为

可以看到，每向后传播一层，则标准差扩大倍，因此，当层数很多时会变为无穷大。

为了解决上述问题，可以设置让每层传播时的方差变为1，即

得：

所以，对于上面的代码，可以改造为每层的权重为均值0，标准差，这样就可以避免每层标准差成倍增长的问题。

代码实现：

修改MLP类initialize中初始化权重的方法

def initialize(self):
    for m in self.modules():
        if isinstance(m, nn.Linear):
            nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))

layer:0, std:0.9974957704544067 layer:1, std:1.0024365186691284     ... layer:98, std:1.1617802381515503 layer:99, std:1.2215303182601929 tensor([[-1.0696, -1.1373,  0.5047,  ..., -0.4766,  1.5904, -0.1076],         [ 0.4572,  1.6211,  1.9659,  ..., -0.3558, -1.1235,  0.0979],         ...,         [-0.5871, -1.3739, -2.9027,  ...,  1.6734,  0.5094, -0.9986]],        grad_fn=)

 

4.1.2.常用初始化方法

对于之前手动进行权值初始化，PyTorch提供了一些常用的权值初始化方法

Xavier初始化

方差一致性：保持数据尺度维持在恰当范围，通常方差为1
激活函数：饱和函数，如Sigmoid， Tanh

方差的计算法则为：

，  

其中，表示输入层的神经元数量，表示输出层的神经元数量。

代码实现：

在之前的代码基础上，首先在MLP类forward方法中，为每层添加sigmoid激活函数

def forward(self, x):
    for (i, linear) in enumerate(self.linears):
        x = linear(x)

# 添加sigmoid激活函数
        x = torch.sigmoid(x)

 

然后，修改MLP类initialize中初始化权重的方法为Xavier初始化

def initialize(self):
    for m in self.modules():
        if isinstance(m, nn.Linear):
            # 权重初始化使用xavier均匀分布进行初始化
            nn.init.xavier_uniform_(m.weight.data)

layer:0, std:0.20717598497867584 layer:1, std:0.1237645372748375     ... layer:98, std:0.12034578621387482 layer:99, std:0.11722493171691895 tensor([[0.5740, 0.5291, 0.8039,  ..., 0.4145, 0.3551, 0.7414],         [0.5740, 0.5291, 0.8039,  ..., 0.4145, 0.3551, 0.7414],         ...,         [0.5740, 0.5291, 0.8039,  ..., 0.4145, 0.3551, 0.7414]],        grad_fn=)

 

可以看到标准差始终控制在0.12左右

Kaiming初始化

差一致性：保持数据尺度维持在恰当范围，通常方差为1
激活函数： ReLU及其变种

方差的计算法则为：

 对于ReLU变种：

其中，表示输入层的神经元数量，a为激活函数在负半轴的斜率

代码实现：

在之前的代码基础上，首先在MLP类forward方法中，每层激活函数改为relu

def forward(self, x):
    for (i, linear) in enumerate(self.linears):
        x = linear(x)
        # 使用relu激活函数
        x = torch.relu(x)

然后，修改MLP类initialize中初始化权重的方法为Kaiming初始化

def initialize(self):
    for m in self.modules():
        if isinstance(m, nn.Linear):
            # 权重初始化使用kaiming正太分布进行初始化
            nn.init.kaiming_normal_(m.weight.data)

layer:0, std:0.826629638671875 layer:1, std:0.8786815404891968     ... layer:98, std:0.6579315066337585 layer:99, std:0.6668476462364197 tensor([[0.0000, 1.3437, 0.0000,  ..., 0.0000, 0.6444, 1.1867],         [0.0000, 0.9757, 0.0000,  ..., 0.0000, 0.4645, 0.8594],         ...,         [0.0000, 1.1807, 0.0000,  ..., 0.0000, 0.5668, 1.0600]],        grad_fn=)

 

可以看到标准差始终控制在0.5-1左右

 

十种初始化方法

1. Xavie r均匀分布
2. Xavie r正态分布
3. Kaiming均匀分布
4. Kaiming正态分布
5. 均匀分布
6. 正态分布
7. 常数分布
8. 正交矩阵初始化
9. 单位矩阵初始化
10. 稀疏矩阵初始化

4.2.损失函数

4.2.1.损失函数概述

损失函数：衡量模型输出与真实标签的差异

常见的概念：

损失函数(Loss Function)： ，即一个样本预测值与真实值差异

代价函数(Cost Function)： ，即所有样本的差异的平均

目标函数(Objective Function)： Regularization，即代价函数+正则项

通常将损失函数和代价函数统称为损失函数，使用代价函数的计算结果。

4.2.2.交叉熵损失函数

交叉熵 = 信息熵 + 相对熵

熵：亦称为信息熵，用来描述事件的不确定性，事件越不确定，熵越大

熵的计算公式：

自信息：，表示单个事件的不确定性

相对熵：用来衡量两个分布之间的差异

计算公式：

其中表示真实的分布，表示模型输出的分布

交叉熵：

对相对熵公式展开得：

所以，，即 交叉熵 = 信息熵 + 相对熵

由于信息熵为真实分布计算而来，可以看做常数，因此，优化交叉熵等价于优化相对熵。

 

PyTorch中的交叉熵：

nn.CrossEntropyLoss

功能： nn.LogSoftmax ()与nn.NLLLo s s ()结合，进行交叉熵计算
• weight：各类别的loss设置权值
• ignore _index：忽略某个类别
• reduction ：计算模式，可为none/sum /mean
none- 逐个元素计算，返回每个元素的loss
sum- 所有元素求和，返回标量
mean- 加权平均，返回标量

reduction的三个模式之前是由size_average和reduce计算而来，但是现在不需要这两个参数了

nn.CrossEntropyLoss(weight=None,
size_average=None,
ignore_index=-100,
reduce=None,
reduction=‘mean’‘) 

这里计算交叉熵损失的过程：

当有权重时：

代码实现：

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
import numpy as np

# 构建数据，输入有三个样本，这里的输入即为跑完模型后的output
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
# 二分类任务，设置每个样本的标签
target = torch.tensor([0, 1, 1], dtype=torch.long)

# 交叉熵损失函数测试
# 定义损失函数，分别设置三种计算模式
loss_f_none = nn.CrossEntropyLoss(weight=None, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=None, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=None, reduction='mean')

# 利用损失函数计算数据
loss_none = loss_f_none(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print("Cross Entropy Loss:\n ", loss_none, loss_sum, loss_mean)

Cross Entropy Loss:   tensor([1.3133, 0.1269, 0.1269]) tensor(1.5671) tensor(0.5224)

 

手动计算某个样本的交叉熵验证结果：

代码实现：

# 指定计算第几个样本
idx = 0

# 获取指定的样本输入
input_1 = inputs.numpy()[idx]      # [1, 2]
# 获取指定样本的标签
target_1 = target.numpy()[idx]              # [0]

# 第一项
x_class = input_1[target_1]

# 第二项
# map是对每个元素进行相同的操作
sigma_exp_x = np.sum(list(map(np.exp, input_1)))
log_sigma_exp_x = np.log(sigma_exp_x)

# 输出loss
loss_1 = -x_class + log_sigma_exp_x

print("第一个样本loss为: ", loss_1)

第一个样本loss为:  1.3132617

 

如何为交叉熵设置每个类别的权重？

代码实现：

# 设置每个类别的权重
weights = torch.tensor([1, 2], dtype=torch.float)

loss_f_none_w = nn.CrossEntropyLoss(weight=weights, reduction='none')
loss_f_sum = nn.CrossEntropyLoss(weight=weights, reduction='sum')
loss_f_mean = nn.CrossEntropyLoss(weight=weights, reduction='mean')

# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print("\nweights: ", weights)
print(loss_none_w, loss_sum, loss_mean)

weights:  tensor([1., 2.]) tensor([1.3133, 0.2539, 0.2539]) tensor(1.8210) tensor(0.3642)

 

可以看出，当设置权重后，对应类别的损失就会乘以权重，但是在计算平均交叉熵损失时，利用的是加权平均的计算方式

 

4.2.3.其他损失函数

1. nn.NLLLoss
功能： 只是对输入的对应类别数据取负号
• weigh t：各类别的loss设置权值
• igno re _index：忽略某个类别
• reduc tion ：计算模式，可为none/sum /mean
none-逐个元素计算
sum-所有元素求和，返回标量
mean-加权平均，返回标量

nn.NLLLoss(weight=None,
size_average=None,
ignore_index=-100,
reduce=None,
reduction='mean') 

计算公式：

代码实现：

# 构建数据
inputs = torch.tensor([[1, 2], [1, 3], [1, 3]], dtype=torch.float)
target = torch.tensor([0, 1, 1], dtype=torch.long)

 

# 使用NLLLoss损失函数

loss_f_none_w = nn.NLLLoss(weight=None, reduction='none')
loss_f_sum = nn.NLLLoss(weight=None, reduction='sum')
loss_f_mean = nn.NLLLoss(weight=None, reduction='mean')

# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print("NLL Loss", loss_none_w, loss_sum, loss_mean)

NLL Loss tensor([-1., -3., -3.]) tensor(-7.) tensor(-2.3333)

 

2. nn.BCELoss
功能： 二分类交叉熵
注意事项：输入值取值在[0,1]
• weigh t：各类别的loss设置权值
• igno re _index：忽略某个类别
• reduc tion ：计算模式，可为none/sum /mean
none-逐个元素计算
sum-所有元素求和，返回标量
mean-加权平均，返回标量

nn.BCELoss(weight=None,
size_average=None,
reduce=None,
reduction='mean’) 

计算公式：

代码实现：

# 定义数据，这里的输入数据并非在0-1之间
inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

# 将输入数据压缩到0-1之间
inputs = torch.sigmoid(inputs)

loss_f_none_w = nn.BCELoss(weight=None, reduction='none')
loss_f_sum = nn.BCELoss(weight=None, reduction='sum')
loss_f_mean = nn.BCELoss(weight=None, reduction='mean')

# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print("BCE Loss", loss_none_w, loss_sum, loss_mean)

BCE Loss tensor([[0.3133, 2.1269],         [0.1269, 2.1269],         [3.0486, 0.0181],         [4.0181, 0.0067]]) tensor(11.7856) tensor(1.4732)

 

3. nn.BCEWithLogitsLoss
功能：结合Sigmoid与二分类交叉熵，相当于在二分类之前先进行sigmoid
注意事项：网络最后不加sigmoid函数
• pos _weigh t ：正样本的权值
• weigh t：各类别的loss设置权值
• igno re _index：忽略某个类别
• reduc tion ：计算模式，可为none/sum /mean
none-逐个元素计算
sum-所有元素求和，返回标量
mean-加权平均，返回标量

nn.BCEWithLogitsLoss(weight=None,
size_average=None,
reduce=None, reduction='mean',
pos_weight=None) 

计算公式：

代码实现：

# 定义数据，这里的输入数据并非在0-1之间

inputs = torch.tensor([[1, 2], [2, 2], [3, 4], [4, 5]], dtype=torch.float)
target = torch.tensor([[1, 0], [1, 0], [0, 1], [0, 1]], dtype=torch.float)

loss_f_none_w = nn.BCEWithLogitsLoss(weight=None, reduction='none')
loss_f_sum = nn.BCEWithLogitsLoss(weight=None, reduction='sum')
loss_f_mean = nn.BCEWithLogitsLoss(weight=None, reduction='mean')

# forward
loss_none_w = loss_f_none_w(inputs, target)
loss_sum = loss_f_sum(inputs, target)
loss_mean = loss_f_mean(inputs, target)

# view
print(loss_none_w, loss_sum, loss_mean)

tensor([[0.3133, 2.1269],         [0.1269, 2.1269],         [3.0486, 0.0181],         [4.0181, 0.0067]]) tensor(11.7856) tensor(1.4732)

 

4. nn.L1Loss
功能： 计算inputs与target之差的绝对值

• reduction ：计算模式，可为none/sum/mean
none- 逐个元素计算
sum- 所有元素求和，返回标量
mean- 加权平均，返回标量

计算公式：

5. nn.MSELoss
功能： 计算inputs与target之差的平方

计算公式：

代码实现：

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

 

# 输入数据
inputs = torch.ones((2, 2))
# 数据的目标值
target = torch.ones((2, 2)) * 3

# 使用L1Loss损失函数，逐个元素计算模式
loss_f = nn.L1Loss(reduction='none')
loss = loss_f(inputs, target)

print("input:{}\ntarget:{}\nL1 loss:{}".format(inputs, target, loss))

# 使用MSELoss损失函数，逐个元素计算模式
loss_f_mse = nn.MSELoss(reduction='none')
loss_mse = loss_f_mse(inputs, target)

print("MSE loss:{}".format(loss_mse))

input:tensor([[1., 1.],         [1., 1.]]) target:tensor([[3., 3.],         [3., 3.]]) L1 loss:tensor([[2., 2.],         [2., 2.]]) MSE loss:tensor([[4., 4.],         [4., 4.]])

 

6. SmoothL1Loss
功能： 平滑的L1Lo ss
• reduction ：计算模式，可为none/sum/mean
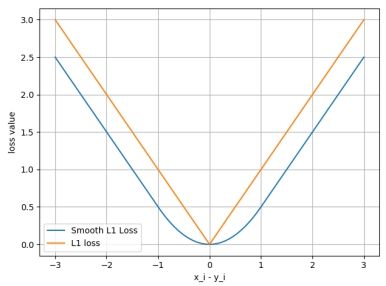
计算公式：， 

SmoothL1Loss与L1Loss图像对比：

代码实现：

在代码中绘制上图

# 输入为-3到3平均取500个数
inputs = torch.linspace(-3, 3, steps=500)
# 目标为与输入形状相同的全0数据
target = torch.zeros_like(inputs)

# 使用SmoothL1Loss损失函数
loss_f = nn.SmoothL1Loss(reduction='none')
loss_smooth = loss_f(inputs, target)

# 直接计算l1正则
loss_l1 = np.abs(inputs.numpy())

# 绘制损失函数的图像
plt.plot(inputs.numpy(), loss_smooth.numpy(), label='Smooth L1 Loss')
plt.plot(inputs.numpy(), loss_l1, label='L1 loss')
plt.xlabel('x_i - y_i')
plt.ylabel('loss value')
plt.legend()
plt.grid()
plt.show()

 

7. nn.KLDivLoss

功能：计算KLD（ divergence）， KL散度，相对熵
注意事项：对于输入，必须是概率的log形式，如通过nn.logsoftmax()变换
• reduction ： none/sum/mean/batchmean
batchmean- batchsize维度求平均值
none- 逐个元素计算
sum- 所有元素求和，返回标量
mean- 加权平均，返回标量

计算公式：

KL散度损失的计算公式：

KLDivLoss损失函数的计算公式：

代码实现：

# 输入数据
inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
# 对输入数据先取对数
inputs_log = torch.log(inputs)
# 目标值
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)

# 使用KLDivLoss损失函数
loss_f_none = nn.KLDivLoss(reduction='none')
loss_f_mean = nn.KLDivLoss(reduction='mean')
loss_f_bs_mean = nn.KLDivLoss(reduction='batchmean')

loss_none = loss_f_none(inputs_log, target)
loss_mean = loss_f_mean(inputs_log, target)
loss_bs_mean = loss_f_bs_mean(inputs_log, target)

print("loss_none:\n{}\nloss_mean:\n{}\nloss_bs_mean:\n{}".format(loss_none, loss_mean, loss_bs_mean))

loss_none: tensor([[ 0.5290, -0.0896, -0.0693],         [-0.0693,  0.5931, -0.1833]]) loss_mean: 0.11844012886285782 loss_bs_mean: 0.35532039403915405

 

可以看到如果采用batchmean模式，是对所有loss求和，然后除以batchsize

可以通过自定义代码计算验证结果

代码实现：

idx = 0
loss_1 = target[idx, idx] * (torch.log(target[idx, idx]) - inputs_log[idx, idx])
print("第一个元素loss:", loss_1)

第一个元素loss: tensor(0.5290)

 

8. nn.MarginRankingLoss

功能： 计算两个向量之间的相似度，用于排序任务
特别说明：该方法计算两组数据之间的差异，返回一个n*n的 loss 矩阵
• margin ：边界值， x1与x2之间的差异值，默认0
• reduction ：计算模式，可为none/sum/mean

计算公式：

y = 1时， 希望比大，当时，不产生loss
y = -1时，希望比大，当x2>x1时，不产生loss

代码实现：

# 定义x1和x2两组数据
x1 = torch.tensor([[1], [2], [4]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)

# 定义目标值y，用来表示希望x1大还是x2大
target = torch.tensor([1, 1, -1], dtype=torch.float)

# 使用MarginRankingLoss损失函数
loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')
loss = loss_f_none(x1, x2, target)

print(loss)

tensor([[1., 1., 0.],         [0., 0., 0.],         [0., 0., 2.]])

 

9. nn.MultiLabelMarginLoss
功能： 多标签边界损失函数，非多分类
举例：四分类任务，样本x属于0类和3类，如一张图片标签既属于人类，又属于马类
• reduction ：计算模式，可为none/sum/mean

计算公式：

其中，i表示非所属标签，j表示所属标签

代码实现：

# 输入数据
x = torch.tensor([[0.1, 0.2, 0.4, 0.8]])
# 目标值，表示数据标签为第0和3类，其他非标签类用-1表示
y = torch.tensor([[0, 3, -1, -1]], dtype=torch.long)

loss_f = nn.MultiLabelMarginLoss(reduction='none')
loss = loss_f(x, y)

print(loss)

tensor([0.8500])

 

手动计算比较

代码实现：

x = x[0]
item_1 = (1-(x[0] - x[1])) + (1 - (x[0] - x[2]))    # [0]
item_2 = (1-(x[3] - x[1])) + (1 - (x[3] - x[2]))    # [3]

loss_h = (item_1 + item_2) / x.shape[0]

print(loss_h)

tensor(0.8500)

 

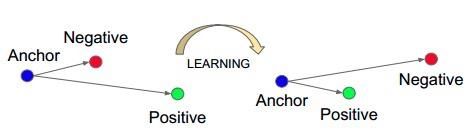
10. nn.TripletMarginLoss
功能：计算三元组损失，人脸验证中常用
• p ：范数的阶，默认为2
• margin ：边界值，默认1
• reduction ：计算模式，可为none/sum/mean

计算公式：

代码实现：

anchor = torch.tensor([[1.]])
pos = torch.tensor([[2.]])
neg = torch.tensor([[0.5]])

loss_f = nn.TripletMarginLoss(margin=1.0, p=1)
loss = loss_f(anchor, pos, neg)

print("Triplet Margin Loss", loss)

Triplet Margin Loss tensor(1.5000)

 

11. nn.HingeEmbeddingLoss
功能：计算两个输入的相似性，常用于非线性embedding和半监督学习
特别注意：输入x应为两个输入之差的绝对值
• margin ：边界值，默认1
• reduction ：计算模式，可为none/sum/mean

计算公式：，其中就是margin的值

代码实现：

inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])

loss_f = nn.HingeEmbeddingLoss(margin=1, reduction='none')
loss = loss_f(inputs, target)

print("Hinge Embedding Loss", loss)

Hinge Embedding Loss tensor([[1.0000, 0.8000, 0.5000]])

 

4.3.优化器-Optimizer

4.3.1.优化器

pytorch的优化器： 管理并更新模型中可学习参数的值，使得模型输出更接近真实标签，即降低loss值，通常采用梯度下降的方式

相关概念：

导数：函数在指定坐标轴上的变化率

方向导数：指定方向上的变化率

梯度：一个向量，方向为方向导数取得最大值的方向

梯度下降算法是机器学习中使用非常广泛的优化算法，也是众多机器学习算法中最常用的优化方法。而随机梯度下降是最常用的优化器。

 

随机梯度下降优化器创建方式：

torch.optim.SGD

主要参数：
• params：管理的参数组
• lr：学习率
• momentum：动量系数

• dampening (float, 可选) – 动量的抑制因子
• weight_decay： L2正则化系数
• nesterov：是否采用NAG

optim.SGD(params, lr=,
momentum=0, dampening=0,
weight_decay=0, nesterov=False)

 

除了随机梯度下降法，pytorch也提供了其他的优化器：

1. optim.Adagrad：自适应学习率梯度下降法
2. optim.RMSprop： Adagrad的改进
3. optim.Adadelta： Adagrad的改进
4. optim.Adam： RMSprop结合Momentum
5. optim.Adamax： Adam增加学习率上限
6. optim.SparseAdam：稀疏版的Adam
7. optim.ASGD：随机平均梯度下降
8. optim.Rprop：弹性反向传播
9. optim.LBFGS： BFGS的改进

4.3.2.学习率

首先，来看梯度下降算法的公式：

其中w为权重，LR为学习率，为梯度

学习率（learning rate）：控制更新的步伐，需要选择合适的学习率，通常为较小的数，如果学习率过大会导致参数无法收敛

例：，利用代码做出其图像，并设置不同的学习率，观察其运行效果

代码实现：

定义损失函数，并绘制其图像

# -*- coding:utf-8 -*-
import torch
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(1)

def func(x_t):
    """
    y = (2x)^2 = 4*x^2      dy/dx = 8x
    """
    return torch.pow(2*x_t, 2)

# init
x = torch.tensor([2.], requires_grad=True)

 

# flag = False
flag = True
if flag:
    # 绘制函数图像
    x_t = torch.linspace(-3, 3, 100)
    y = func(x_t)
    plt.plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
    plt.grid()
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.show()

接下来，利用梯度下降法，绘制其下降过程

代码实现：

# flag = False
flag = True
if flag:
    # 定义三个list，iter_rec存放迭代的次数，loss_rec存放每次迭代后的loss值，x_rec存放迭代后的x的值
    iter_rec, loss_rec, x_rec = list(), list(), list()

    # 设置学习率，可以设置不同的值观察其下降过程
    lr = 0.1    # /1. /.5 /.2 /.1 /.125
    # 设置迭代次数
    max_iteration = 5   # /1. 4     /.5 4   /.2 20 200

    for i in range(max_iteration):
        # 通过初始化的x计算y
        y = func(x)
        # 进行反向传播
        y.backward()

        # 分别打印当前第几次迭代、x的值、x的梯度、y的值
        print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
            i, x.data.numpy()[0], x.grad.data.numpy()[0], y.item()))

        # 将当前x的值添加到x_rec中
        x_rec.append(x.item())

        # x -= lr*x.grad  数学表达式意义:  x = x - lr*x.grad
        x.data.sub_(lr * x.grad)
        # 将x的梯度归零，如果不归零，梯度会叠加
        x.grad.zero_()

        # 将迭代次数添加到iter_rec
        iter_rec.append(i)
        # 将当前的y添加到loss_rec中
        loss_rec.append(y)

    # 绘制第一个图像，为loss随着迭代次数的改变图像
    plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
    plt.xlabel("Iteration")
    plt.ylabel("Loss value")

    # 绘制第二个图像，为函数图像和每次迭代后对应的坐标图
    x_t = torch.linspace(-3, 3, 100)
    y = func(x_t)
    plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
    plt.grid()
    # 对于迭代中每个x，计算其对应的y，并获取计算结果作为list存到y_rec中
    y_rec = [func(torch.tensor(i)).item() for i in x_rec]
    # 绘制梯度下降过程
    plt.subplot(122).plot(x_rec, y_rec, '-ro')
    plt.legend()
    plt.show()

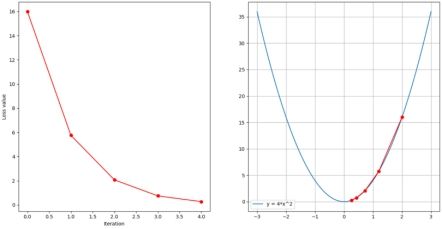
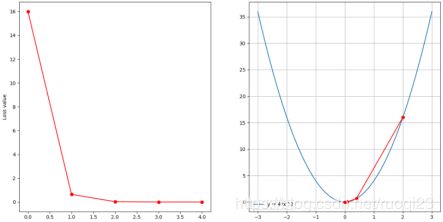
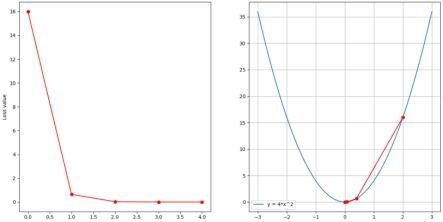
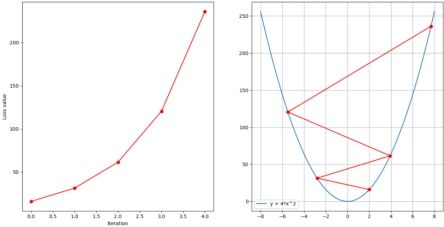
下面为迭代五次，分别设置学习率为0.05,0.1,0.3时的图像

可以看到，当学习率过大时，容易导致发散而无法收敛。

如何选择合适的学习率，可以在一个范围内使用不同的学习率，查看每个学习率的下降曲线

代码实现：

# flag = False
flag = True
if flag:
    # 迭代次数
    iteration = 20
    # 学习率取值的最大最小值
    lr_min, lr_max = 0.01, 0.2  # .5 .3 .2
    # 学习率在最大最小值之间的取值数量
    num_lr = 10

    # 生成学习率的list
    lr_list = np.linspace(lr_min, lr_max, num=num_lr).tolist()
    # 生成与lr_list等长的loss_rec，每个元素为list
    loss_rec = [[] for i in range(len(lr_list))]
    # 定义迭代次数对于的list
    iter_rec = list()

    # 遍历每一个学习率
    for i, lr in enumerate(lr_list):
        # 初始化x
        x = torch.tensor([2.], requires_grad=True)
        for iter in range(iteration):

            y = func(x)
            y.backward()
            x.data.sub_(lr * x.grad)  # x.data -= lr*x.grad
            x.grad.zero_()

            loss_rec[i].append(y.item())

    for i, loss_r in enumerate(loss_rec):
        plt.plot(range(len(loss_r)), loss_r, label="LR: {}".format(lr_list[i]))
    plt.legend()
    plt.xlabel('Iterations')
    plt.ylabel('Loss value')
    plt.show()

在迭代次数为20次情况下，学习率从0.01到0.2之间，选取10个数进行测试，结果如图：

4.3.3.Momentum

Momentum（动量，冲量）：结合当前梯度与上一次更新信息，用于当前更新

先来看看指数加权平均，思想是求取当前时刻的平均值，距离当前时刻越近的参数值所占的权重越大，参考性也越大，越远的参数权重随着指数下降。

指数加权平均计算公式：

其中表示当前时刻的平均值，表示当前时刻的参数值，表示前一个时刻的平均值，是一个超参数，用来表示当前参数的重要性。越大，当前参数权重越低，反之亦然。

假设我们有一年365天的气温数据，把他们化成散点图，如下图所示，这些数据有些杂乱，我们想画一条曲线，用来表征这一年气温的变化趋势，那么我们需要把数据做一次平滑处理。我们可以使用指数加权平均来对数据做平滑。

利用指数加权平均计算公式计算第k天的平均气温得：

在梯度下降中加入Momentum后的参数更新公式：

其中表示第次更新的参数，为学习率，为更新量，m为momentum系数，表示的梯度。

 

 

同样对于气温数据，使用梯度下降中的Momentum更新过程如下：

 

 

代码实现：

在添加momentum后绘制不同学习率对于的下降过程

# -*- coding:utf-8 -*-
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
torch.manual_seed(1)

def func(x):
    return torch.pow(2*x, 2)    # y = (2x)^2 = 4*x^2        dy/dx = 8x

# 迭代次数
iteration = 100
# 设置Momentum
m = 0.9     # .9 .63

# 设置学习率的list
lr_list = [0.01, 0.03]

# 存放momentum的list
momentum_list = list()
# loss的list，长度与学习率list长度一致，每个元素为list
loss_rec = [[] for i in range(len(lr_list))]
# 存放迭代次数的list
iter_rec = list()

# 遍历不同的学习率
for i, lr in enumerate(lr_list):
    # 初始化x的值
    x = torch.tensor([2.], requires_grad=True)

    # 如果学习率是0.03，则设置momentum为0，否则设置为m
    momentum = 0. if lr == 0.03 else m
    # 将momentum存入list中
    momentum_list.append(momentum)

    # 创建随机下降优化器
    optimizer = optim.SGD([x], lr=lr, momentum=momentum)

    for iter in range(iteration):

        y = func(x)
        y.backward()

        # 执行一步更新
        optimizer.step()
        # 清空优化器的梯度
        optimizer.zero_grad()

        # 将当前的y添加到loss的list中
        loss_rec[i].append(y.item())

for i, loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()

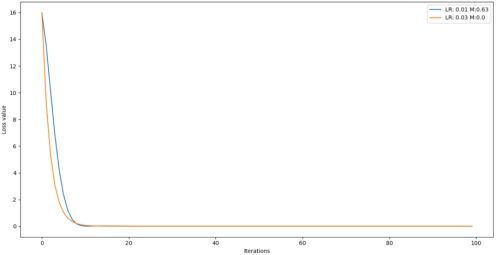
迭代100次，分别设置学习率为0.01和0.03，其中0.01使用momentum，并当m分别取0.9和0.63时的loss结果如下：

通常，momentum动量系数设置为0.9

4.3.4.属性与方法

基本属性：

params_groups：管理的参数组

param_groups = [{'params':param_groups}]

基本方法：

zero_grad()：清空所管理参数的梯度

pytorch特性：张量梯度不自动清零

step()：执行一步更新

add_param_group()：添加参数组

state_dict()：获取优化器当前状态信息字典，用来保存训练过程中的参数信息，防止意外
load_state_dict() ：加载状态信息字典

 

代码实现：

step()方法

# -*- coding: utf-8 -*-
import os
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
import torch
import torch.optim as optim
from tools.common_tools import set_seed

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

# 初始化权重，标准正太分布的2×2数据
weight = torch.randn((2, 2), requires_grad=True)
# 为了计算方便，设置梯度都是1的2×2数据
weight.grad = torch.ones((2, 2))

# 创建随机梯度下降法优化器，为了方便计算，设置学习率为1
optimizer = optim.SGD([weight], lr=1)

#step()方法前后对比
print("weight before step:{}".format(weight.data))
# 执行一次更新
optimizer.step()        # 修改lr=1 0.1观察结果
print("weight after step:{}".format(weight.data))

weight before step:tensor([[0.6614, 0.2669],         [0.0617, 0.6213]]) weight after step:tensor([[-0.3386, -0.7331],         [-0.9383, -0.3787]])

 

# zero_grad()方法前后权重对比
print("weight.grad is \n{}".format(weight.grad))
optimizer.zero_grad()
print("after optimizer.zero_grad(), weight.grad is\n{}".format(weight.grad))

weight.grad is tensor([[1., 1.],         [1., 1.]]) after optimizer.zero_grad(), weight.grad is tensor([[0., 0.],         [0., 0.]])

 

# add_param_group方法添加参数组
# 打印优化器的参数组
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

# 创建新的权重参数
w2 = torch.randn((3, 3), requires_grad=True)
# 通过字典的形式添加到参数组中
optimizer.add_param_group({"params": w2, 'lr': 0.0001})

# 再次打印优化器的参数组
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

optimizer.param_groups is [{'params': [tensor([[0.6614, 0.2669],         [0.0617, 0.6213]], requires_grad=True)], 'lr': 1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}] optimizer.param_groups is [{'params': [tensor([[0.6614, 0.2669],         [0.0617, 0.6213]], requires_grad=True)], 'lr': 1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}, {'params': [tensor([[-0.4519, -0.1661, -1.5228],         [ 0.3817, -1.0276, -0.5631],         [-0.8923, -0.0583, -0.1955]], requires_grad=True)], 'lr': 0.0001, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]

 

# state_dict()方法获取优化器相关状态信息
optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
opt_state_dict = optimizer.state_dict()

# 打印优化器执行前的相关信息
print("state_dict before step:\n", opt_state_dict)

for i in range(10):
    optimizer.step()

# 打印优化器执行后的相关信息
print("state_dict after step:\n", optimizer.state_dict())

# 保存优化器的相关状态
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

state_dict before step:  {'state': {}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [2571404169688]}]} state_dict after step:  {'state': {2571404169688: {'momentum_buffer': tensor([[6.5132, 6.5132],         [6.5132, 6.5132]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [2571404169688]}]}

 

# load_state_dict()方法加载状态信息
optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
# 读取保存的状态信息文件
state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

print("state_dict before load state:\n", optimizer.state_dict())
# 将状态信息加载到优化器中
optimizer.load_state_dict(state_dict)
print("state_dict after load state:\n", optimizer.state_dict())

state_dict before load state:  {'state': {}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [1713556083080]}]} state_dict after load state:  {'state': {1713556083080: {'momentum_buffer': tensor([[6.5132, 6.5132],         [6.5132, 6.5132]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [1713556083080]}]}

 

4.3.5.学习率调整策略

学习率（ learning rate）：控制更新的步伐

在机器学习中，通常在刚开始更新时，希望学习率比较大一点，这样梯度下降的更快，后期学习率小一些，这样更容易收敛。

 

PyTorch提供的学习率调整策略：

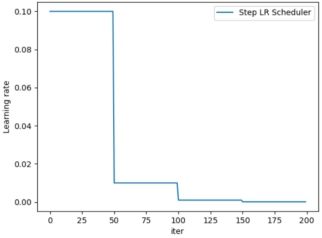
1. torch.optim.lr_scheduler.StepLR
功能：等间隔调整学习率

• optimizer：需要关联的优化器
• step_size：调整间隔数
• gamma：调整系数

• last_epoch：最后一次epoch的索引,默认为-1.

计算公式:

lr_scheduler.StepLR(optimizer, step_size,
gamma=0.1, last_epoch=-1)

代码实现：

# -*- coding:utf-8 -*-
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
torch.manual_seed(1)

# 设置初始学习率
LR = 0.1
# 迭代次数
iteration = 200

# 构建优化器
# 定义初始参数
weights = torch.randn((1), requires_grad=True)
# 定义目标值
target = torch.zeros((1))
# 创建优化器
optimizer = optim.SGD([weights], lr=LR, momentum=0.9)

# flag = 0
flag = 1
if flag:
    # 构建StepLR学习率调整策略，每50步调整一次学习率，并设置调整学习率的系数为0.1
    scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1)  # 设置学习率下降策略

    # 构建学习率的list，迭代次数iter的list
    lr_list, iter_list = list(), list()
    for iter in range(iteration):

        # 将每次的学习率加入list中
        lr_list.append(scheduler_lr.get_lr())
        # 迭代次数加入list中
        iter_list.append(iter)

        # 计算损失函数已经反向求导
        loss = torch.pow((weights - target), 2)
        loss.backward()

        # 执行一步优化并清空梯度
        optimizer.step()
        optimizer.zero_grad()

        # 更新下一个学习率
        scheduler_lr.step()

    # 绘制学习率的图像
    plt.plot(iter_list, lr_list, label="Step LR Scheduler")
    plt.xlabel("iter")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

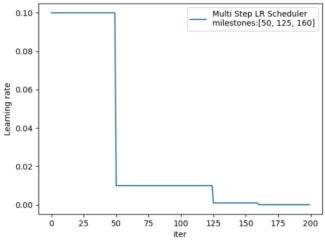
2. MultiStepLR
功能：按给定间隔调整学习率
• milestones：设定调整时刻数，如[50, 125, 160]

• gamma：调整系数

计算公式：

  lr_scheduler.MultiStepLR(optimizer,milestones,

 gamma=0.1, last_epoch=-1)

代码实现

# flag = 0
flag = 1
if flag:

    milestones = [50, 125, 160]
    scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.1)

    lr_list, iter_list = list(), list()
    for iter in range(iteration):

        lr_list.append(scheduler_lr.get_lr())
        iter_list.append(iter)

        loss = torch.pow((weights - target), 2)
        loss.backward()

        optimizer.step()
        optimizer.zero_grad()

        scheduler_lr.step()

    plt.plot(iter_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))
    plt.xlabel("iter")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

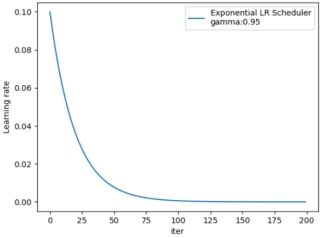
3. ExponentialLR
功能：按指数衰减调整学习率
• gamma：指数的底

计算公式：

lr_scheduler.ExponentialLR(optimizer, gamma,
last_epoch=-1)

代码实现：

# flag = 0
flag = 1
if flag:
    # 以每次0.95倍的系数下降
    gamma = 0.95
    scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

    lr_list, iter_list = list(), list()
    for iter in range(iteration):

        lr_list.append(scheduler_lr.get_lr())
        iter_list.append(iter)

        loss = torch.pow((weights - target), 2)
        loss.backward()

        optimizer.step()
        optimizer.zero_grad()

        scheduler_lr.step()

    plt.plot(iter_list, lr_list, label="Exponential LR Scheduler\ngamma:{}".format(gamma))
    plt.xlabel("iter")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

4. CosineAnnealingLR
功能：余弦周期调整学习率
• T_max：下降周期，即余弦中从最高下降到最低点的周期
• eta_min：学习率下限，即最低点的值

lr_scheduler.CosineAnnealingLR(optimizer,T_max,

eta_min=0, last_epoch=-1)

代码实现：

# flag = 0
flag = 1
if flag:
    # 下降周期为50
    t_max = 50
    scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=t_max, eta_min=0.)

    lr_list, iter_list = list(), list()
    for iter in range(iteration):

        lr_list.append(scheduler_lr.get_lr())
        iter_list.append(iter)

        loss = torch.pow((weights - target), 2)
        loss.backward()

        optimizer.step()
        optimizer.zero_grad()

        scheduler_lr.step()

    plt.plot(iter_list, lr_list, label="CosineAnnealingLR Scheduler\nT_max:{}".format(t_max))
    plt.xlabel("iter")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

5. ReduceLRonPlateau
功能：监控指标，当指标不再变化则调整
• mode： min /max 两种模式，通常min监控loss，max监控acc准确率
• factor：调整系数
• patience：“耐心 ”，接受几次不变化
• cooldown：“冷却时间”，停止监控一段时间
• verbo se：是否打印日志
• min _lr：学习率下限
• eps：学习率衰减最小值

lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1,

patience=10,
verbose=False, threshold=0.0001,
threshold_mode='rel', cooldown=0,

min_lr=0, eps=1e-08)

代码实现：

# flag = 0
flag = 1
if flag:
    # 假设loss一直都是0.5，即loss不下降
    loss_value = 0.5
    # 假设准确率一直都是0.9，即准确率不上升
    accuray = 0.9

    # 设置调整系数，即每次调整的倍数
    factor = 0.1
    # 设置模式，min表示监控是否继续下降
    mode = "min"
    # 设置连续多少次不变换后调整
    patience = 10
    # 冷却时间，即每次调整后停止监控次数
    cooldown = 10
    # 学习率下限，即学习率调整到这个值后将不再调整
    min_lr = 1e-4
    # 是否打印日志
    verbose = True

    scheduler_lr = optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, mode=mode, patience=patience, cooldown=cooldown, min_lr=min_lr, verbose=True)

    for iter in range(iteration):

        optimizer.step()
        optimizer.zero_grad()

        # 可以设置在5次后loss下降了，观察调整学习率的时间
        if iter == 5:
            loss_value = 0.4

        # 注意，这里在更新下一个学习率的时候，需要将上一个学习率作为标量传入
        scheduler_lr.step(loss_value)

Epoch    16: reducing learning rate of group 0 to 1.0000e-02. Epoch    37: reducing learning rate of group 0 to 1.0000e-03. Epoch    58: reducing learning rate of group 0 to 1.0000e-04.

 

6. LambdaLR
功能：自定义调整策略
• lr_lambda： function or list

lr_scheduler.LambdaLR(optimizer, lr_lambda,
last_epoch=-1)

实现代码：

# flag = 0
flag = 1
if flag:
    # 初始化学习率
    lr_init = 0.1

    # 初始化权重，设置两组权重
    weights_1 = torch.randn((6, 3, 5, 5))
    weights_2 = torch.ones((5, 5))

    # 创建优化器，两组权重设置相同的初始学习率
    optimizer = optim.SGD([
        {'params': [weights_1]},
        {'params': [weights_2]}], lr=lr_init)

    # 设置两组学习率变换策略
    lambda1 = lambda iter: 0.1 ** (iter // 20)      # 每20次迭代学习率×0.1
    lambda2 = lambda iter: 0.95 ** iter             # 每次迭代学习率×0.95

    # 创建LambdaLR，并为两个参数组分别设置两种学习率调整策略的list
    scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])

    lr_list, iter_list = list(), list()
    for iter in range(iteration):

        optimizer.step()
        optimizer.zero_grad()

        scheduler.step()

        # lr_list中每个元素是由两个学习率组成的list
        lr_list.append(scheduler.get_lr())
        iter_list.append(iter)

        print('iter:{:5d}, lr:{}'.format(iter, scheduler.get_lr()))

    plt.plot(iter_list, [i[0] for i in lr_list], label="lambda 1")
    plt.plot(iter_list, [i[1] for i in lr_list], label="lambda 2")
    plt.xlabel("iter")
    plt.ylabel("Learning Rate")
    plt.title("LambdaLR")
    plt.legend()
    plt.show()

iter:    0, lr:[0.1, 0.095] iter:    1, lr:[0.1, 0.09025] ... iter:  199, lr:[1.0000000000000006e-11, 3.5052666248828703e-06]

最后，对于学习率的初始化，通常可以设置较小的数，如：0.01、0.001、0.0001等，也可以搜索最大的学习率。