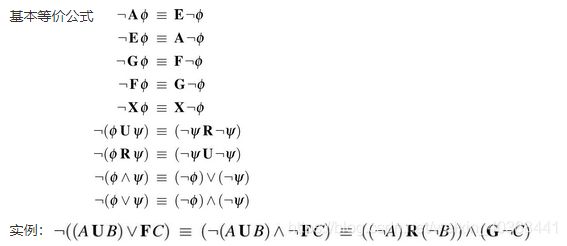Model checking Part III

第四章 时态逻辑

概念：时态逻辑是用于指定系统动态行为的一种形式，建模为kripke结构。

组成：时态逻辑有时间运算符和路径量词组成，并且可与布尔连接词组合。

本章主要内容

• 介绍CTL* 的语义语法
• 介绍CTL* 中包含的时态逻辑
• 对所介绍的时态逻辑做简单的比较

4.1 计算树逻辑CTL*

计算树的形成： 给定kripke结构M中的初始状态s0，通过将结构展开到具有根s0的树中来形成树。

注：由于转换关系是完全的，即每个状态都存在后继状态，且计算树表示从初始状态所有可能的执行，所以计算树是无限的。

CTL* 公式组成：路径量词和时间运算符

路径量词：

Aφ—“所有计算路径”（来自给定状态的所有路径都具有属性φ）
Eφ—“存在计算路径”（来自给定状态的至少一条路径具有属性φ）

时间运算符：保持沿着树给定的无限路径的属性

Xp—“next time p”（要求命题p保持在路径的第二状态）
Fp—“eventually p”or“in the future p”（断言属性p保持在路径的某个状态）
Gp—“always p”or“globally p”（指定命题p保持在路径上的每个状态）
p U q—“p until q”（如果路径上有第二个属性q持有的状态，则该属性保持不变；而在路径上的每个先前状态(如果存在的话)，保持第一个属性p）
p R q—“p release q”（要求第二属性q沿着路径保持直到并包括第一属性p所在的第一状态。但是，第一个属性p最终不需要保留）

上述时间运算符沿着无限路径验证如下：

实例：设前面的计算树最左、右路径为π1、π2，则以下式子成立：

路径量词和时间运算符的区别：路径量词描述状态的属性（状态公式）；时间运算符描述路径的属性（路径公式）。

4.2 CTL* 的语法和语义

4.2.1 CTL* 语法

CTL* 中存在两种类型的公式：状态公式和路径公式

令AP为原子命题的集合，公式规则如下：
状态公式：
A1：如果p∈AP，则p是状态公式。
A2：如果f和g是状态公式，则¬f，f∨g和f∧g是状态公式。
A3：如果f是路径公式，则Ef和Af是状态公式。

路径公式：
A4：如果f是状态公式，则f也是路径公式。
A5：如果f和g是路径公式，则f、f∧g、f∨g、Xf、Ff、Gf、fUg、fRg也是路径公式。

CTL* 即为满足上述规则的一组状态公式，因此，CTL* 公式是布尔命题、带有前导路径量词的时态公式及其布尔的组合。

4.2.2 CTL* 语义

基本符号介绍：假设kripke结构M是五元组(S, S0, R, AP, L)

π：s0、s1、s2、…，为M上从s0状态开始的无限路径。
πi：π中以si为起始状态的路径。
╞：
—若f为状态公式，则M，s╞ f表示f在M中的s状态时保持不变；
—若f为路径公式，则M，π╞ f表示f在M中沿着路径π保持不变。
≡：逻辑等价符。无论f和g同时为状态公式或路径公式，只要f ≡ g，那么两者的表达式等价。

╞的具体释义：

注：上述16条释义，其中公式的可满足性和有效性是逻辑中的经典问题。但模型检测问题相反，对于f和给定的kripke结构，需要测定M是否为f的模型，即M╞ f。

语义特性：

1. 通过操作符∨，¬，X，U和E足以表达任何其他CTL * 公式（{∨，¬，X，U，E}称为CTL* 的完备集）
   如图所示：
   
2. 当系统初始状态不唯一时，释义16可能会存在一些问题
   

4.2.3 否定范式(NFF)

否定范式(NNF)是逻辑公式的一种句法形式，其中否定只适用于原子命题。

定理：每个CTL* 公式都能转换为NNF形式（通常需要∧，∨，E，A，X，U和R）。

4.3 基于CTL* 的时态逻辑

本节介绍了CTL* 的几个重要的子逻辑，其中CTL、ACTL* 、ACTL是分支时间逻辑；LTL是线性时间逻辑。

注：分为两组的依据是在分支时间逻辑中，路径量化符可以重复量化计算树中从不同状态可以到达的路径；而在线性时间逻辑中，单一通用路径量化符可以量化从初始状态开始的所有路径。

下面分别介绍各子逻辑的语法语义，由于与CTL* 的包含关系，受到CTL* 语法的限制，但在某些方面更为简单。

4.3.1 分支时间逻辑CTL

计算树逻辑CTL是CTL * 的子逻辑，其中路径量词和时间运算符总是成对出现。

注：由于路径量词和时间运算符成对出现这一特性，当我们考虑CTL子公式时，需要满足这一特性，且与CTL* 子公式不同，CTL的子公式必须是状态公式。
例：AXEXp的CTL子公式是AXEXp，EXp和p；而在CTL* 层面考虑的话，还包括XEXp和Xp。

语法：

B1：如果p∈AP，则p是CTL公式
B2：如果f是CTL公式，则¬f，AXf，EXf，AFf，EFf，AGf和EGf是CTL公式
B3：如果f和g是CTL公式，则f∧g，f∨g，A(f U g)，E(f U g)，A(f R g)和E(f R g)是CTL公式

语义：

逻辑公式等价表示（AX、EX、AF、EF、AG、EG、AU、EU、AR和ER）：

由等价表示可将CTL定义为基于EX，EG，EU运算符的逻辑（即CTl完备集为{∨，¬，EX，EG，EU}），语义如下：

4.3.2 通用计算树逻辑ACTL* 和ACTL

1. ACTL*

ACTL* 是CTL* 的子逻辑，只允许使用通用路径量化符A。且为了能将A用E的否定表示，规定ACTL* 必须包含在NFF中。
语法：

状态公式：
C1：如果p∈AP，那么p和¬p是ACTL* 状态公式。
C2：如果f和g是ACTL* 状态公式，则f∨g和f∧g是ACTL* 状态公式。
C3：如果f是ACTL* 路径公式，则Af是ACTL* 状态公式。

路径公式：
C4：如果f是ACTL* 状态公式，那么f也是ACTL* 路径公式。
C5：如果f和g是ACTL* 路径公式，那么f∨g，f∧g，Xf，Ff，Gf，f U g，f R g是ACTL* 路径公式。

ACTL* 即为满足上述规则的一组状态公式。

ECTL* ：ECTL* 的定义与ACTL* 类似，只不过将A替换成了E。由A与E的关系可以看出ACTL* 与ECTL* 为否定互换关系。

注：对于ACTL* 和ECTL* ，时间运算符X、U和R足以表示所有其他时间运算符，即完备集为{∨，¬，X，U，R}。

2. ACTL

ACTL逻辑自然结合了ACTL* 和CTL的句法限制。
语法：

如果p∈AP，则p和¬p为ACTL公式。
如果f是ACTL公式，则AXf、AFf和AGf是ACTL公式。
如果f和g是ACTL公式，则f∧g，f∨g，A(f U g)，A(f R g)也是ACTL公式。

注：ACTL公式可以转换为使用AX、AU和AR的公式。

4.3.3 线性时间逻辑(LTL)

概念：LTL逻辑，即线性时间逻辑，不是指kripke结构的计算树，而是指树的单个计算集（可视为树的一条线性子路径）。

形式：Af，其中f是LTL路径公式，不包括路径量词的CTL* 路径公式，这意味着这样的路径公式可能只包含原子命题作为状态子公式。

注：由CTL* A4可知在CTL* 逻辑中状态公式也是路径公式，即若f为状态公式，那么f、Af和Ef也为路径公式。但在LTL路径公式中，我们剔除了包含路径量词的CTL* 路径公式，即剔除了Af、Ef。所以说LTL路径公式实际上是CTL* 的特殊情况。

LTL路径公式定义：

E1：如果p∈AP，则p是LTL路径公式。
E2：如果f是LTL路径公式，则¬f，Xf，Ff和Gf是LTL路径公式。
E3：如果f和g是LTL路径公式，则f∧g，f∨g，f U g和f R g是LTL路径公式。

由于f R g ≡ ¬（¬f U ¬g），Ff ≡ true U f和Gf ≡ ¬Ff，所以LTL可用X、U来进行定义，即LTL完备集为{∨，¬，X，U}。

注：有些情况下会省略单一通用量化词A，例如M ╞ f表示M ╞ Af。

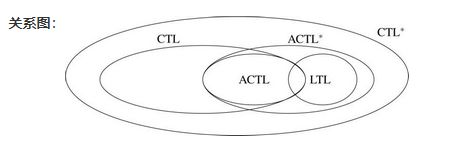
4.3.4 CTL* 各部分间的关系

举例：
(1) LTL公式AFGp（沿着每条路径的属性，总会出现状态p并且后续状态将永远保持p），不包含在CTL逻辑中。
(2) CTL公式AG(EFp)，不包含在LTL逻辑中。
(3) CTL* 公式A(FGp)∨AG(EFp),既不包含在LTL，也不包含在CTL逻辑中。
(4) ACTL公式AFAGa和AFAXa，不包含在LTL逻辑中。
(5) ACTL* 包含LTL逻辑，即ACTL* 比LTL逻辑更有表现力，例：ACTL * 公式AGp∨AGq在LTL中不可表达。
(6) CTL公式AGEFp和AG¬AFp，不包含在ACTL逻辑中（由于ACTL只能包含路径量化词A，且由于包含于NFF，ACTL的否定必须作用于原子命题）。
(7) 有些在CTL中可表示的LTL属性在ACTL中是不可表达的,例：A¬Fp

4.4 集合原子命题与集合语义的时态逻辑

本小节提出了一种将逻辑公式与满足该公式的赋值集相关联的一种方法，这种方法在用kripke结构描述的时态逻辑中表现为用Kripke结构状态的集合来识别为真的公式。

应用：

可以根据满足f的状态来描述CTL* 状态公式f的语义，定义

来将f与其成立的状态集相关联。

为了直接引用kripke结构的状态，扩展了CTL* 的语法和语义：

语法拓展：
为了能用状态集表示，将状态集纳入原子CTL* 公式，设Q = {s1，…，sn}⊆S，表示Q中保持的状态属性集，则可添加以下语法
— 如果{s1，…，sn}⊆S，那么{s1，…，sn}是一个称为集合原子命题的CTL* 状态公式。
语义拓展：

公式举例：M，s0╞ EX{s, t}表示从s0开始可以在一步内到达s或t状态。

4.5 公平

在上一章中已经提到了系统建模的公平性，在这小节我们将公平的概念引入了时态逻辑中。
具有公平约束的kripke结构M定义为：

M =（S，S0，R，L，AP，F），其中S，S0，R，L和AP定义如前。公平约束的集合是F = {P1，…，Pk}⊆2∧s，其中Pi ⊆ S。

注：有时可将不具公平约束的结构转换为具有公平约束的结构，并同时保留被视为计算的路径集合，可通过令F = {S}来实现这一目的。

公平路径：

令π= s0，s1，…为M中的路径，定义

对于每个P∈F，若满足关系式inf(π) ∩ P≠∅，则称路径π是公平的。

将公平性概念引入时态逻辑中

1. 在具有集合原子命题的CTL* 的情况下，用
   
   表示路径的公平性（每个P必须包含一个在路径上无限出现的状态）。
2. 将公平性加入Eφ和Aφ的表示中，可用公式：

第一个表示存在满足φ的公平路径；第二个表示任意公平路径都满足φ。

3. 为了能让其他时态逻辑更一般的表示公平性，拓展了CTL* 语义，称之为公平语义：
   

4.6 反例

概念：反例生成是模型检验的核心特征，它区别于其他验证方法，如定理证明和抽象解释。在其最简单的形式中，反例是显示违反规范的痕迹。因此，反例为开发该系统的工程师提供了宝贵的反馈。

4.7 安全性和活跃性

概念：安全属性保证永远不会发生错误，而活跃属性确保最终会发生好事。

实例：

安全属性：AGp
活跃属性：AFp和A(p U q)

区分：

反例提供了一种区分安全性和活跃性的自然方法。
通常情况下：
—安全属性是能通过有限无环反例反驳的属性；
—活跃属性是能通过套索形式反例反驳的属性（有限状态）。