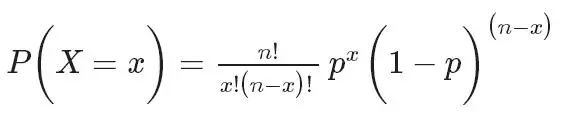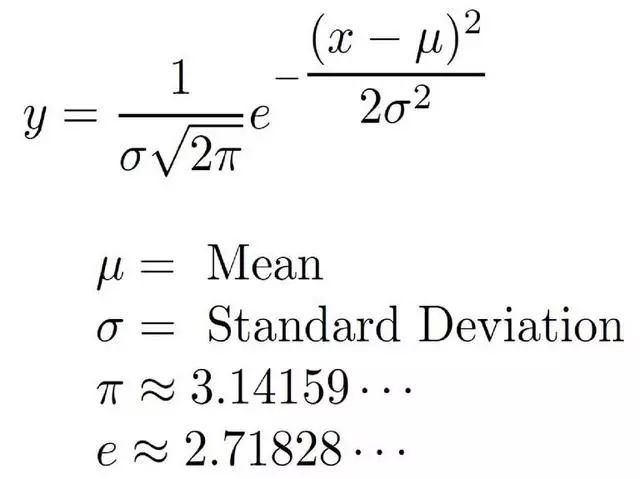数据分析必须掌握的概率分布!建议收藏!
重磅干货,第一时间送达
![]()
Data Science (数据科学)作为现如今最炙手可热的领域之一,越来越受到人们的关注。而数据分析背后充满了概率统计的知识。因此,打下良好的概率论基础是必须的。
数据类型
‘巧妇难为无米之炊’,数据分析的‘主料’即为数据。当我们对一组数据作分析的时候,一定要明确的是,这组数据只是研究对象(population)中的一部分样本(sample)。我们只是对一部分样本进行分析,然后去推测出整个对象的规律。
首先,需要明确的是:数据分析中,数据量越多,样本越大,结果越准确。
那有人会问,既然这样,为什么不搜集海量的数据呢?大部分的工作只是为了找到一个近似的规律,而且过大的数据量会带来收集费用的飙升、处理难度和时间的增加。因此,数据处理第一步,我们要试着去平衡数据量和处理的耗费(金钱与时间)。
数据类型大体分为两种:数值(如房价)和类别(如品牌,姓名等)。
而数值型数据可细分为离散(不连续)和连续数据。
图1:概率分布类型
概率分布可以很好的展现数据的内在规律,图1中就总结归纳了大部分的概率分布类型。接下来,我们就简单的理解一下这些概率分布。
伯努利分布(Bernoulli Distribution)
伯努利分布是概率分布中最简单、最基本也是最基础的分布形式之一。我们从图1可以看到很多复杂的概率分布都是基于伯努利分布。
怎么理解伯努利分布呢?单次实验和两种情况。
伯努利分布代码
伯努利分布
举例说明:假如女人生孩子,生男孩概率是60%,生女孩概率是40%。那么,伯努利分布就是--- 生一次孩子,生男孩的概率为 p = 60%, 而生女孩的概率为 1 - p = 40%。如上图所示。
关键词:单次实验,两种情况分类
二项式分布(Binomial Distribution)
基于前面介绍的伯努利分布,可以衍生出二项式分布:n重伯努利试验「成功」次数的离散概率分布。继续以生孩子为例:
生一次孩子,生男孩的概率为 p = 60%, 而生女孩的概率为 1 - p = 40%。
假如生了 n 个孩子,其中男孩为 x 个,女孩为(n - x)的概率。
重点:
单次试验重复多次;
单次试验为伯努利分布;
各次试验相互独立。也就是说每次生孩子,生男孩和生女孩概率不变,都是60%和40%。
二项式分布公式
如果我们假定生了 n 个孩子,其中男孩是4个(固定值),那么随着n的变化,二项式分布的概率图会怎么变呢?
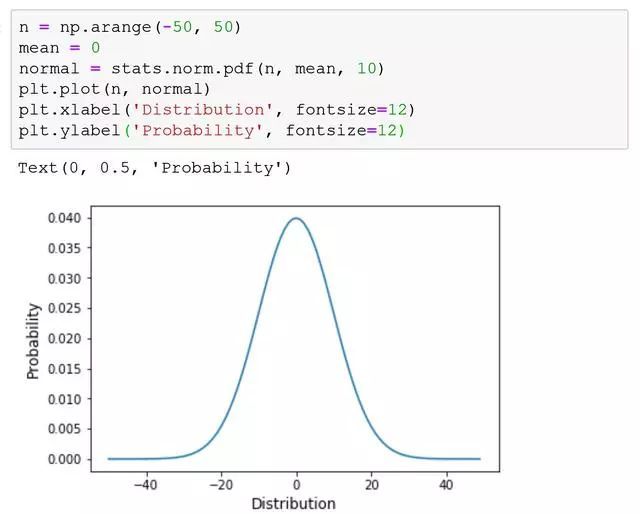
二项式分布代码
二项式分布图
如上图所示,如果生了4孩子且全是男孩,概率0.6的四次方 = 0.1296。当生了6个孩子的时候,有四个是男孩的概率达到了0.311。并且随着孩子越来越多,几乎不可能保证只生了4个男孩,其他都是女孩,毕竟单次生男孩的概率要大一些。
正态分布(高斯分布)
正态分布是最最最重要的分布之一,在数据分析领域也是最常见的分布之一。我们生活中很多常见现象都遵循正态分布,比如说收入分布,身高分布等等。
正态分布
举个例子,比如说你去相亲,而你最在意的标准是相亲对象的身高,所以你对相亲对象的身高做了统计,你会发现大部分人的身高会集中在一定的范围呢,而只有很少的人会很高或者很矮。
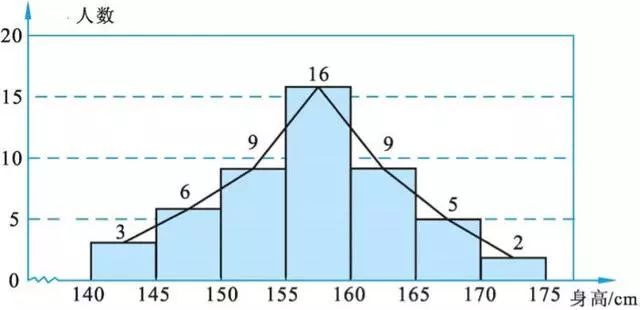
身高分布
大部分的女生会集中在155到160 cm之间,这也很符合我们日常所见。
正态分布的特点:
正态分布左右对称;
正态分布曲线下的面积为1,也就是说正态分布的所有情况出现的概率之和为1。
正态分布
正态分布中,最重要的两个参数是 平均值 μ 和标准差 σ。也就是说如果告诉我们这两个参数,我们就可以知道正态分布下每种情况出现的概率。
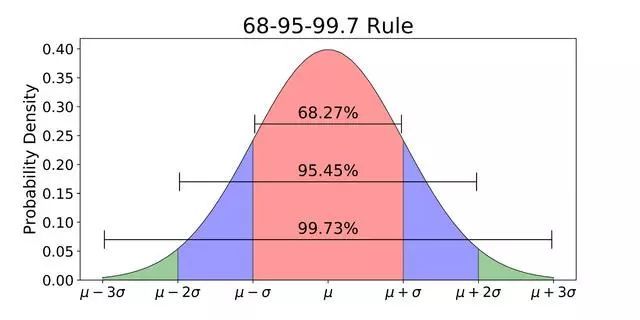
正态分布
上面这张图是什么意思呢?具体来说就是,满足正态分布,68.27%的情况都会出现在平均值正负1个标准差以内。比如说,女生身高平均值是160 cm, 标准差为5 cm。那么,68.27%的女生的身高会在155 到 165 cm之间。95.45%的女生身高在150 (平均值减去2个标准差)到170 cm之间。
在机器学习领域,很多的机器学习模型也是遵循正态分布的,比如说:
高斯朴素贝叶斯分类器 (Gaussian Naive Bayes Classifier)
线性判别分析(Linear Discriminant Analysis)
二次判别分析(Quadratic Discriminant Analysis)
基于最小二乘法的回归模型(Least Squares based regression models)
泊松分布(Poisson Distribution)
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。--------------维基百科
泊松分布
泊松分布的计算公式如上。λ是单位时间(或单位面积)内随机事件的平均发生率,比如说你预测一天平均有300人来医院就诊。而医院医生的满负荷量是400人,那么出现一天有400人就诊的概率则满足泊松分布。
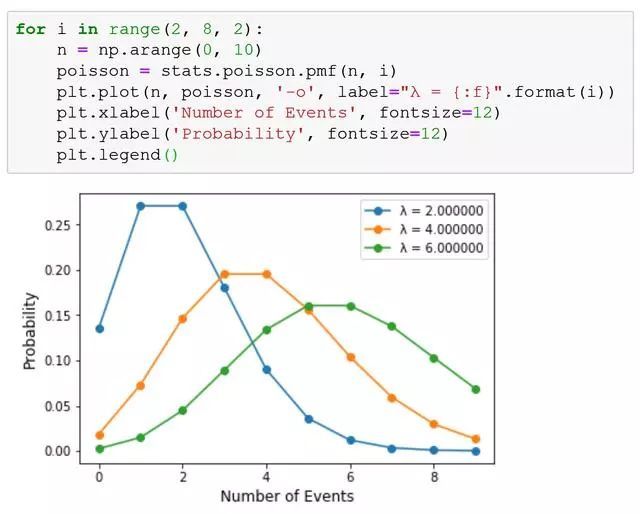
泊松分布
知道泊松分布有什么用呢?根据单位时间内出现概率的大小可以做出决策。比如说,当你举办一次抽奖活动,你的设计是平均每天只有5(λ)个一等奖产生,那么,就可以算出来一天产生了10个一等奖概率是多少?0.018132788707821854。
也就是说一天出现10次一等奖概率只为1.8%。可以放心了,不会超预算了!
总结
概率学在人类生活决策中随处可见。很多人过着不满意的生活,可能就是放弃了概率选择权的原因。什么概率选择权呢?
比如说,有个富豪说给你两种选择:
直接给你500万;
你可以抽奖,概率是50%机会拿到2000万,而50%概率什么也没有;
那么你会选择什么呢?
大部分人会选择第一种。因为落袋为安,我可承受不起第二种什么也没抽到的情况,我会后悔死。
但是,我们从概率学来说,第一种的期望值是500万 (出现的情况 * 出现的概率 之和:500 * 100%),而第二种的期望值是(50% * 2000 + 50% * 0 = 1000万)。第二种选择的期望值明显要高于第一种。这个比较抽象,和具体现实没联系。
那么,这种情况呢?
比如说:你在大公司年薪10万,工作稳定。现在有一个创业公司过来挖你,给出的工资是5万,但是有股票(股票只能上市之后兑现,价值5000万)。但是创业都是九死一生,成功上市的概率可能只有1%。
这种情况你会如何选择呢?如果可以,请留言告诉我你的答案,我们也好看看你是否也放弃了概率选择权。
![]()
喜欢文章,点个在看 ![]()