感知器算法与神经网络，及反向传播算法的推导

姓名：Jyx
班级：csdn人工智能直通车-5期
描述：这是本人在学习人工智能时的学习笔记，加深理解

1. 感知器模型
   1.1 感知器模型的推广
2. 神经网络
3. 反向传播算法
   

感知器模型(wiki)

一个简单的感知器算法可以表示如下

yy=sgn(wTx+b)=sgn(w∗Tx∗) 或者,where w∗=[wT,b]T,x∗=[xT,1]T y = sgn ⁡ ( w T x + b )  或者 y = sgn ⁡ ( w ∗ T x ∗ ) , w h e r e   w ∗ = [ w T , b ] T , x ∗ = [ x T , 1 ] T

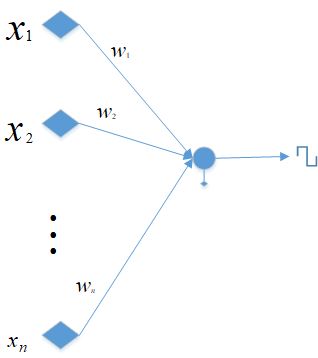
出于简化考虑，本文采用第二种表达方式，如无特别说明一般用 w,x w , x 代替 w∗,x∗ w ∗ , x ∗ 。
感知器的代价函数定义为:

J(w)=∑x∈Y(δxwTx),δx={−1,+1,x∈ω1x∈ω2 J ( w ) = ∑ x ∈ Y ( δ x w T x ) , δ x = { − 1 , x ∈ ω 1 + 1 , x ∈ ω 2

ω1,ω2 ω 1 , ω 2 代表类别， Y Y 代表错误分类的样本的集合。
显然代价函数总是正的。
采用梯度下降法，权重更新公式为

w(t+1)=w(t)−ρt∂J(w)∂w∣∣∣w=w(t)=w(t)−ρt∑x∈Y(δxx) w ( t + 1 ) = w ( t ) − ρ t ∂ J ( w ) ∂ w | w = w ( t ) = w ( t ) − ρ t ∑ x ∈ Y ( δ x x )

算法描述：

• 随机选择 w(0) w ( 0 ) , 选择 ρ0 ρ 0
• t=0 t = 0
• 重复
  
  • Y=∅ Y = ∅
  • For i=1 to N F o r   i = 1   t o   N
    If δxiw(t)Txi≥0 then Y=Y∪{xi} I f   δ x i w ( t ) T x i ≥ 0   t h e n   Y = Y ∪ { x i }
  • End For E n d   F o r
  • w(t+1)=w(t)−ρt∑x∈Yδxx w ( t + 1 ) = w ( t ) − ρ t ∑ x ∈ Y δ x x
  • 调整 ρt→ρt+1 ρ t → ρ t + 1
  • t = t+ 1
• 直到 Y=∅ Y = ∅

这不是一个标准的梯度下降过程，因为函数 j(w) j ( w ) 随着训练的进行一直在改变。但算法依然收敛。

感知器模型的推广

异或问题

简单的感知器模型只能处理线性可分的问题，著名的异或问题感知器算法就不能解决。为此，可以使用两层感知器，
两层感知器的局限：
两层感知器的处理能力依旧有限：两层感知器可以分离由多面体区域的并集构成的类，而不能分离这些区域的并集。
为此，我们可以选择三层感知器。

神经网络

上面讨论通过增加感知器的层数来增强感知器的分类能力，但另一方面我们也可以改变感知器的其它方面来增强他的分类能力，比如激活函数。这就是神经网络。
在查找资料的过程中，找到一个很有用的博客专题：深度神经网络基本问题的原理详细分析和推导，里面具体描述了神经网络的方方面面

关于激活函数的一个定理

整个机器学习中最重要的一个部分就是优化，优化可以看成是在一定损失函数下的拟合问题。通用逼近定理给出了一些拟合的结论。通用逼近定理这里就不罗列了，有兴趣参考wiki，这里摘录一段网上一篇blog对通用逼近定理的解释

一个仅有单隐藏层的神经网络。在神经元个数足够多的情况下，通过特定的非线性激活函数(包括sigmoid，tanh等)，足以拟合任意函数。这使得我们在思考神经网络的问题的时候，不需要考虑：我的函数是否能够用神经网络拟合，因为他永远可以做到——只需要考虑如何用神经网络做到更好的拟合（摘自https://blog.csdn.net/zpcxh95/article/details/69952020）

反向传播算法

反向传播算法从根本上而言是一种多元函数的链式法则的应用。其中也没有高深的推导，只是有层窗户纸让人看不真切
这里力图把本人理解的关键点写清楚。
推荐一篇比较形象的推导反向传播算法

一个简单的神经网络定义如下

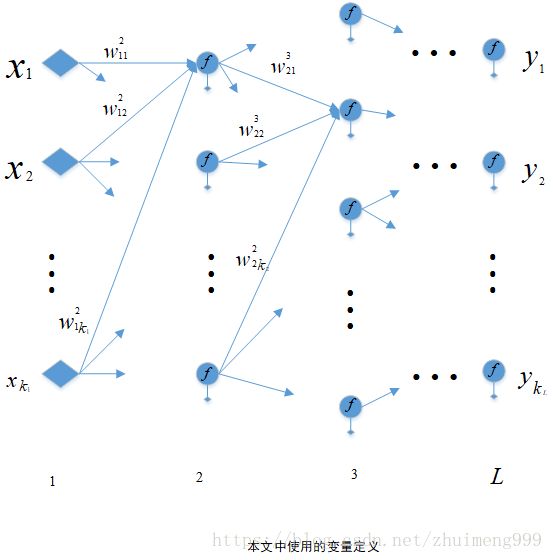
在本文推倒中假定网络共有 L(1,⋯,L) L ( 1 , ⋯ , L ) 层，每层有 ki k i 个神经元，有两个特例：对于第一层输入层 k1 k 1 就等于输入向量的特征维数，对于最后一层输出层 kL k L 就等于输出向量的维数，又假定输入向量共有 N(x1,⋯,xN) N ( x 1 , ⋯ , x N ) 个， fli f i l 表示第 l l 层的第 i i 个激活函数， wlij w i j l 表示第 l l 层第 i i 个神经元的第 j j 个权向量， bl b l 表示第 l l 层的偏置。 y^ y ^ 表示网络的输出。 vli v i l 表示第 l l 层第 i i 个神经元的输出

一般形式

按照上面的定义，每一层的输出可以表示为上一层输出的函数，即

定义辅助变量则vliy^iξlivli=fli(∑j=1kl−1wlijvl−1j+bli),l>1=vLi=∑j=1l−1wlijvl−1j+bli=fli(ξli),l>1(1)(2)(3) (1) v i l = f i l ( ∑ j = 1 k l − 1 w i j l v j l − 1 + b i l ) , l > 1 y ^ i = v i L 定义辅助变量 (2) ξ i l = ∑ j = 1 l − 1 w i j l v j l − 1 + b i l 则 (3) v i l = f i l ( ξ i l ) , l > 1

note: 这里有个重点 wlij和vl−1j w i j l 和 v j l − 1 是独立的变量，这意味着对 ξli ξ i l 求导时 vl−1j v j l − 1 可以看作常量
同一般的反向传播算法这个名字暗示的那样，我们从最后一层开始往回计算梯度，即先计算 wLij w i j L 的梯度，再依次 wl−1ij,⋯,w2ij w i j l − 1 , ⋯ , w i j 2

1. 第 L L 层
对于损失 L(y,y^) L ( y , y ^ ) ，可以写成 vLi(y^i=vLi) v i L ( y ^ i = v i L ) 的函数

L(y,y^)∂L∂wLij∂L∂bLi=L(y,y1^,y2^,⋯,ykl^)=L(y,vL1,vL2,⋯,vLkL)=∂L∂vLi∂vLi∂wLij=∂L∂vLi∂vLi∂ξLi∂ξLi∂wLij=∂L∂vLi∂vLi∂bLi=∂L∂vLi∂vLi∂ξLi∂ξLi∂bLi(4)(5)(6) L ( y , y ^ ) = L ( y , y 1 ^ , y 2 ^ , ⋯ , y k l ^ ) (4) = L ( y , v 1 L , v 2 L , ⋯ , v k L L ) (5) ∂ L ∂ w i j L = ∂ L ∂ v i L ∂ v i L ∂ w i j L = ∂ L ∂ v i L ∂ v i L ∂ ξ i L ∂ ξ i L ∂ w i j L (6) ∂ L ∂ b i L = ∂ L ∂ v i L ∂ v i L ∂ b i L = ∂ L ∂ v i L ∂ v i L ∂ ξ i L ∂ ξ i L ∂ b i L

利用2式和3式，可以得到

∂ξLi∂wLij∂ξLi∂bLi∂vLi∂ξLi=vL−1j=1=f′Li(ξli) ∂ ξ i L ∂ w i j L = v j L − 1 ∂ ξ i L ∂ b i L = 1 ∂ v i L ∂ ξ i L = f i ′ L ( ξ i l )

所以5式和6式可以化简成

∂L∂wLij∂L∂bLi=L′(vLi)f′Li(ξli)vL−1j=L′(vLi)f′Li(ξli) ∂ L ∂ w i j L = L ′ ( v i L ) f i ′ L ( ξ i l ) v j L − 1 ∂ L ∂ b i L = L ′ ( v i L ) f i ′ L ( ξ i l )

2. l<L l < L 层
当 l<L l < L 时，根据神经网络的构成，每一层都只和下一层有关。迭代递归下去可以知道，损失 L(y,y^) L ( y , y ^ ) 总可以写成某一层的函数，即

L(y,y^)=L(y,vl1,vl2,⋯,vlkl)(7) (7) L ( y , y ^ ) = L ( y , v 1 l , v 2 l , ⋯ , v k l l )

注意式（7）和式（3）虽然形式不同，但确实是同一个函数，只不过展开深度的不同。
因为式（7）和式（3），根据上面的推导过程，立即可以得到

∂L∂wlij∂L∂bli=∂L∂vLi∂vli∂wlij=∂L∂vli∂vli∂ξli∂ξli∂wlij=∂L∂vli∂vli∂bli=∂L∂vli∂vli∂ξli∂ξli∂bli(5)(6) (5) ∂ L ∂ w i j l = ∂ L ∂ v i L ∂ v i l ∂ w i j l = ∂ L ∂ v i l ∂ v i l ∂ ξ i l ∂ ξ i l ∂ w i j l (6) ∂ L ∂ b i l = ∂ L ∂ v i l ∂ v i l ∂ b i l = ∂ L ∂ v i l ∂ v i l ∂ ξ i l ∂ ξ i l ∂ b i l

∂L∂vli ∂ L ∂ v i l 并不像第 L L 层那样好求，因为网络太复杂并且网络结构不确定，直接展开求解显然不可能，这时，反向 传播算法中的传播 就来了，考虑网络的结构，我们可以 一层一层递归解决
假定第 l+1 l + 1 层已经解决，即 ∂L∂vl+1i ∂ L ∂ v i l + 1 已知。
考虑第 l+1 l + 1 层，综合式（1）和式（7）

L(y,y^)vl+1i利用多元函数的链式法则 ∂L∂vli=L(y,vl+11,vl+12,⋯,vl+1kl+1)=fl+1i(∑j=1klwl+1ijvlj+bl+1i),i=1,⋯,N=∑j=0kl+1∂L∂vl+1j∂vl+1j∂vli=∑j=0kl+1∂L∂vl+1j∂vl+1j∂ξl+1j∂ξl+1j∂vli=∑j=0kl+1∂L∂vl+1jl+1层梯度f′l+1j(ξl+1j)容易求出wl+1ji已知(7)(8) (7) L ( y , y ^ ) = L ( y , v 1 l + 1 , v 2 l + 1 , ⋯ , v k l + 1 l + 1 ) v i l + 1 = f i l + 1 ( ∑ j = 1 k l w i j l + 1 v j l + b i l + 1 ) , i = 1 , ⋯ , N 利用多元函数的链式法则  ∂ L ∂ v i l = ∑ j = 0 k l + 1 ∂ L ∂ v j l + 1 ∂ v j l + 1 ∂ v i l = ∑ j = 0 k l + 1 ∂ L ∂ v j l + 1 ∂ v j l + 1 ∂ ξ j l + 1 ∂ ξ j l + 1 ∂ v i l (8) = ∑ j = 0 k l + 1 ∂ L ∂ v j l + 1 ⏟ l + 1 层 梯 度 f j ′ l + 1 ( ξ j l + 1 ) ⏟ 容 易 求 出 w j i l + 1 ⏟ 已 知

这样 ∂L∂vli ∂ L ∂ v i l 已经求出，带入5，6式即可求出 l l 层梯度