数据结构-堆的基本操作
堆(heap)也被称为优先队列(priority queue)。队列中允许的操作是先进先出(FIFO),在队尾插入元素,在队头取出元素。而堆也是一样,在堆底插入元素,在堆顶取出元素,但是堆中元素的排列不是按照到来的先后顺序,而是按照一定的优先顺序排列的。这个优先顺序可以是元素的大小或者其他规则。如图一所示就是一个堆,堆优先顺序就是大的元素排在前面,小的元素排在后面,这样得到的堆称为最大堆。最大堆中堆顶的元素是整个堆中最大的,并且每一个分支也可以看成一个最大堆。同样的,我们可以定义最小堆,如图二所示。
堆的存储
堆可以看成一个二叉树,所以可以考虑使用二叉树的表示方法来表示堆。但是因为堆中元素按照一定的优先顺序排列,因此可以使用更简单的方法——数组——来表示,这样可以节省子节点指针空间,并且可以快速访问每个节点。堆得数组表示其实就是堆层级遍历的结果,
堆的特点
堆存储在下标为0开始的数组中,因此在队中给定下标为i的节点时:
1)如果i=0,则节点i是根节点,且没有左右子树。否则节点i的双亲节点为(i-1)/2;
2) 若2*i+11,则节点i的左孩子为节点2*1+1,否则无左孩子
3) 若2*i+21,则节点的右孩子为2*i+2,否则无右孩子 以下是堆的基本操作
头文件(heap.h)
#pragma once
#include
//对于大堆,就是a>b
typedef int (*Compare)(HeapType a,HeapType b);
typedef struct Heap
{
HeapType data[HeapMaxSize];
size_t size;
Compare cmp;
}Heap;
//初始化堆,决定是大堆还是小堆
void HeapInit(Heap* heap,Compare cmp);
//销毁堆
void HeapDestory(Heap* heap);
//插入
void HeapInsert(Heap* heap,HeapType value);
//删除堆顶元素
void HeapRemove(Heap* heap)
源代码如下(heap.c)
#include <stdlib.h>
#include <stdio.h>
#include <stdlib.h>
#include "heap.h"
//初始化
void HeapInit(Heap* heap,Compare cmp)
{
//非法输入
if(heap==NULL)
{
return ;
}
heap->size=0;
heap->cmp=cmp;
return ;
}
//销毁堆
void HeapDestory(Heap* heap)
{
//非法输入
if(heap==NULL)
{
return;
}
heap->size=0;
heap->cmp=NULL;
return ;
}
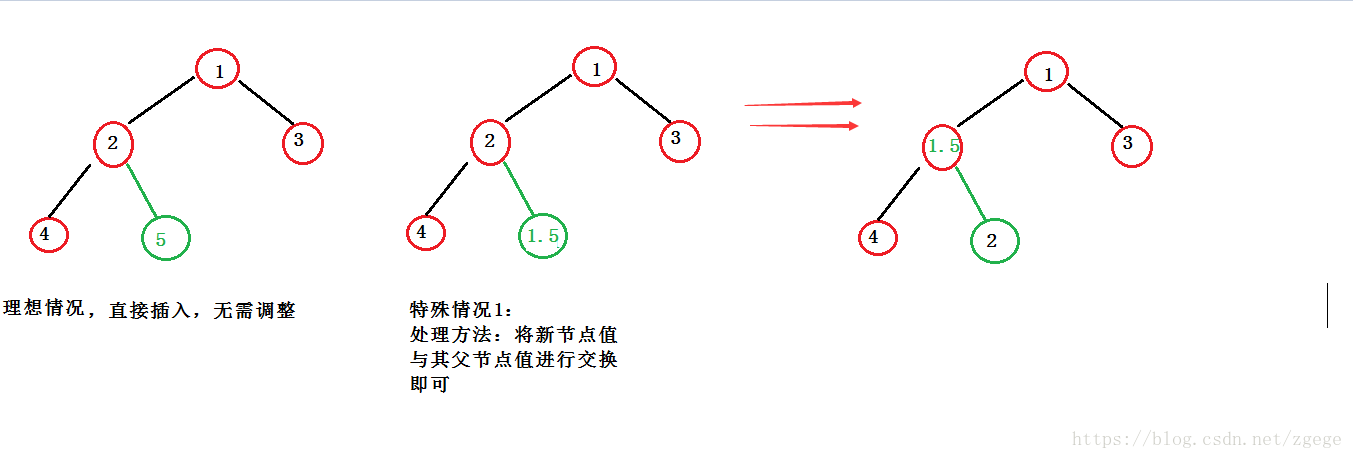
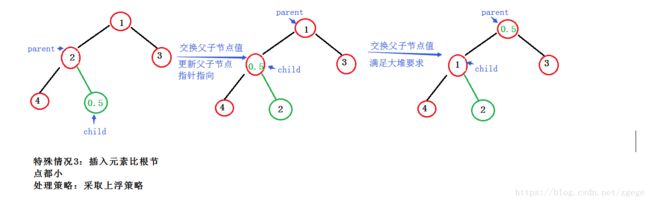
堆的插入
在一个堆中插入元素,可能会影响堆的结构,(要保证插入之前是一个大堆,插入之后依然是一个大堆),此时需要对堆的 结构进行上浮操作
//上浮函数
void Adjustup(Heap* heap,size_t index)
{
//定义一个孩子节点和一个父节点
size_t child=index;
size_t parent=(child-1)/2;
while(child>0)
{
//如果父节点大于子节点,则进行值交换(小堆)
if(!heap->cmp(heap->data[parent],heap->data[child]))
{
Swap(&heap->data[parent],&heap->data[child]);
}
else
{
//如果发现某一个位置,发现child和parent满足堆要求
//则停止上浮,因为上面的元素都符合堆要求
break;
}
//更新child和parent的指向(上浮)
child=parent;
parent=(child-1)/2;
}
return;
}
//插入函数
void HeapInsert(Heap* heap,HeapType value)
{
//非法输入
if(heap==NULL)
{
return ;
}
//堆满了,无法插入
if(heap->size>HeapMaxSize)
{
return ;
}
//将新元素插在数组有效元素的末尾
heap->data[heap->size++]=value;
//开始上浮调整。使其满足堆的要求
AdjustUp(heap,heap->size-1);
return ;
}
//取堆顶元素
int HeapRoot(Heap* heap,HeapType* value)
{
//非法输入
if(heap==NULL)
{
return 0 ;
}
if(heap->size==0)
{
return 0;
}
*value=heap->data[0];
return 1;
}
删除堆顶元素
1,将堆中最后一个元素代替堆顶元素
2,将堆中元素个数减一,此时相当于堆中最后一个元素被删除了
3,此时结构可能破坏再向下调整,使其符合堆的性质
//下沉函数
void AdjustDown(Heap* heap,size_t index)
{
size_t parent=index;
size_t child=2*parent+1;
while(childsize)
{
//存在右子树,并且右子树比左子树更符合堆的要求,
//
//则将child->右子树
if(child+1size && heap->cmp(heap->data[child+1],heap->data[child]))
{
child=child+1;
}
if(heap->cmp(heap->data[child],heap->data[parent]))
{
Swap(&heap->data[child],&heap->data[parent]);
}
else
{
break;
}
parent=child;
child=2*parent+1;
}
}
//删除堆顶元素
void HeapErase(Heap* heap)
{
if(heap==NULL)
{
return ;
}
if(heap->size==0)
{
return ;
}
//交换堆顶元素和最后一个元素
Swap(&heap->data[0],&heap->data[heap->size-1]);
//--size
--heap->size;
//从根节点出发进行下沉调整
AdjustDown(heap,0);
}
判断是否是空堆,如果不是空堆,将元素个数打印出来
size_t HeapSize(Heap* heap)
{
//非法输入
if(heap==NULL)
{
return 0;
}
return heap->size;
}
准备函数如下
//为小堆 准备的函数
int Less(HeapType a,HeapType b)
{
return a1:0;
}
//为大堆打造的比较函数
int Greater(HeapType a,HeapType b)
{
return a>b?1:0;
}
//交换函数
void Swap(HeapType* a,HeapType* b)
{
HeapType tmp=*a;
*a=*b;
*b=tmp;
return;
}
//打印函数
void HeapPrintChar(Heap* heap,const char *msg)
{
printf("%s\n",msg);
size_t i=0;
for(;isize;i++)
{
printf( "[%c]|[%d]->",heap->data[i],i);
}
printf("NULL\n");
return ;
} 以下为测试代码
//if 1
#include