机器学习——分类问题(2020最新版)
直接使用梯度下降法去做逻辑回归,相当于完成底层实现。
直接调用sklearn的话,简单很多,具体实现无法学习到。
一、逻辑回归(Logistic Regression)
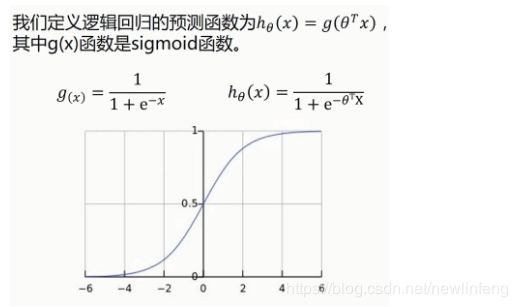
逻辑回归是用来处理分类问题的
Sigmoid/Logistic Function:
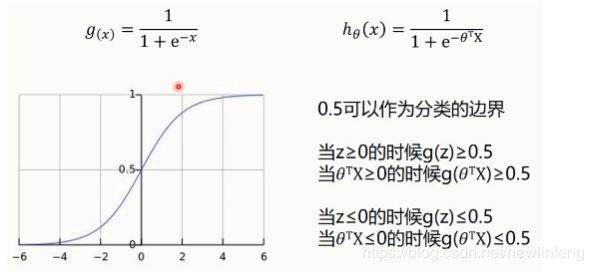
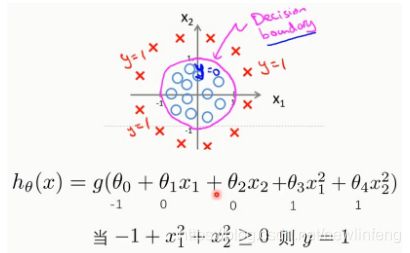
1、决策边界
case 1:
case 2:
case 3:
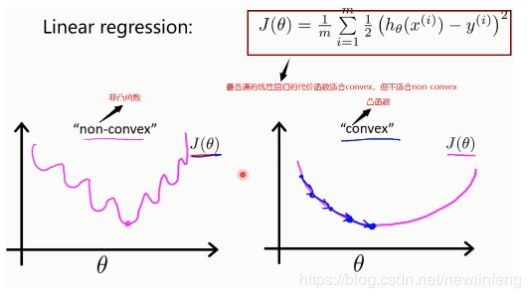
2、逻辑回归的代价函数
(1) 所以对于non-convex func来说,梯度下降法的代价函数并不适合这种问题求解,需要新的代价函数。
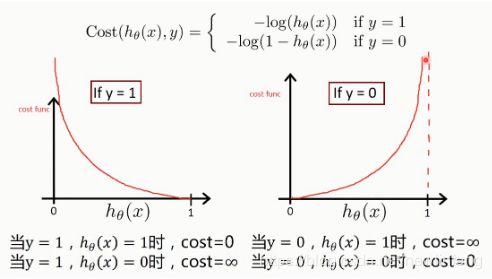
(2) 由上图可知,预测正确,cost的值越小(为0),预测错误,cost的值越大(为无穷大)。
(3) 这个就是逻辑回归的代价函数的公式,在后面深度学习里面使用的交叉熵,也是这个公式。
使用梯度下降法,下面是求导过程:
所以得到@j的每次更替的值用如下式子进行赋值:
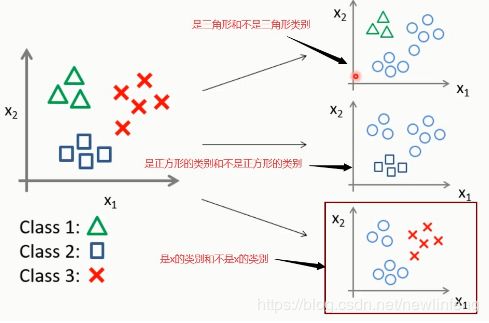
3、多分类问题如何解决
逻辑回归一般是用来做这种二分类的问题的,那么对于多分类的情况,如何做?
可以做三个分类边界,如下图:
4、逻辑回归的正则化
——————————————————————————————————————————
在上面的介绍如何使用逻辑回归进行分类后,下面讲述如何去评价分类后的结果(评价指标)
——————————————————————————————————————————
5、正确率(precision)/召回率(recall)/F1指标
举个例子,去理解正确率、召回率、F1-score:
因此,综合考虑precision和recall才是可行的,所以使用F1-Score来评价:
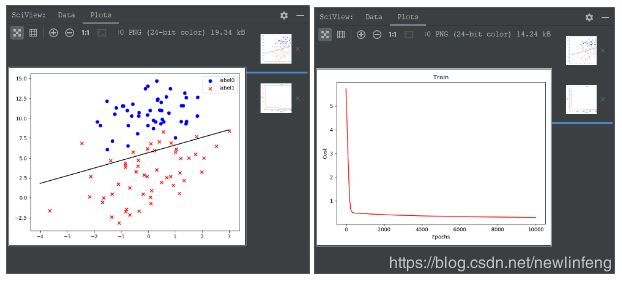
使用最基本的梯度下降法来实现线性逻辑回归:
# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
FileName: sks_logistic_regression_method
Author: newlinfeng
Date: 2020/7/28 0028 11:47
Description: 使用sklearn实现分类问题中的逻辑回归
-------------------------------------------------------------------------------
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt(r"LR-testSet.csv", delimiter=",")
x_data = data[:, :-1]
y_data = data[:, -1]
#为了画这个散点图
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
#切分不同类型的数据
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
#画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
#数据处理,添加偏执项
x_data = data[:, :-1]
y_data = data[:, -1, np.newaxis]
#给样本添加偏执项
X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)
#逻辑回归的函数
def sigmoid(x):
return 1.0/(1+np.exp(-x))
#逻辑回归的代价函数
def cost(xMat, yMat, ws):
left = np.multiply(yMat, np.log(sigmoid(xMat*ws))) #multiply()是对于矩阵元素的位置进行相乘(矩阵的形状必须一模一样)
right = np.multiply(1-yMat, np.log(1-sigmoid(xMat*ws)))
return np.sum(left + right)/-(len(xMat))
#
def gradAscent(xArr, yArr):
if scale == True:
xArr = preprocessing.scale(xArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr)
lr = 0.001 #学习率
epochs = 10000 #迭代周期
costList = [] #保存cost的值
#计算数据行列数
#行代表数据个数,列代表权值个数
m, n = np.shape(xMat)
#初始化权值矩阵
ws = np.mat(np.ones((n, 1)))
for i in range(epochs+1):
#xMat和weights矩阵相乘
h = sigmoid(xMat*ws)
#计算误差
ws_grad = xMat.T*(h-yMat)/m
ws = ws - lr*ws_grad
if i%50 == 0:
costList.append(cost(xMat, yMat, ws))
return ws,costList
#训练模型,得到权重和cost值的变化
ws, costList = gradAscent(X_data, y_data)
print(ws)
#是否做参数标准化
if scale == False:
#画图决策边界
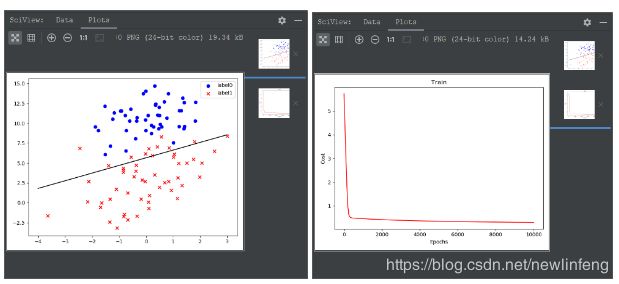
plot()
#画那条线
x_test = [[-4], [3]]
y_test = (-ws[0] - x_test*ws[1])/ws[2]
plt.plot(x_test, y_test, 'k')
plt.show()
#画下loss值的变化
x = np.linspace(0, 10000, 201)
plt.plot(x, costList, c='r')
plt.title("Train")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.show()
#预测
def predict(x_data, ws):
if scale == True:
x_data = preprocessing.scale(x_data)
xMat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x>=0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(X_data, ws)
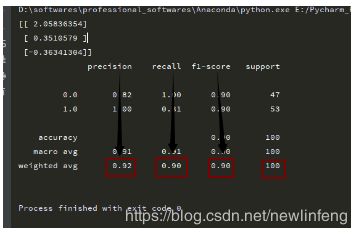
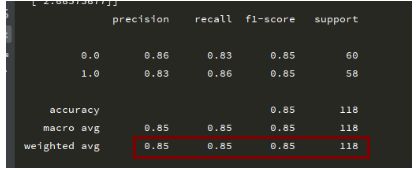
print(classification_report(y_data, predictions))相应的评价指标值为:
使用sklearn来实现线性逻辑回归:
# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
FileName: skl_logistic_regression_method
Author: newlinfeng
Date: 2020/7/28 0028 16:27
Description: 使用sklearn实现逻辑回归
-------------------------------------------------------------------------------
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn import linear_model
#数据是否需要标准化
scale = False
#载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:, :-1]
y_data = data[:, -1]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
#切分不同类型的数据
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
#画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
plot()
plt.show()
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
if scale == False:
#画决策边界
plot()
x_test = np.array([[-4], [3]])
y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0]/logistic.coef_[0][1])
plt.plot(x_test, y_test, 'k')
plt.show()
predictions = logistic.predict(x_data)
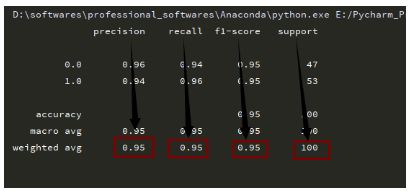
print(classification_report(y_data, predictions))结果比上面好一些:
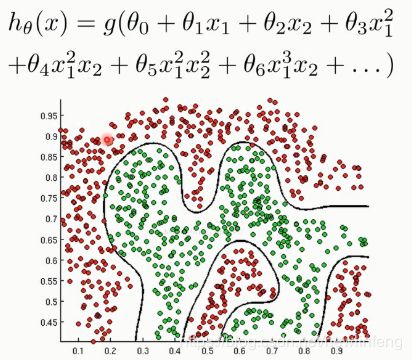
6、非线性逻辑回归
使用梯度下降法实现非线性逻辑回归:
# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
FileName: gradAscent_logistic_regression
Author: newlinfeng
Date: 2020/7/28 0028 17:07
Description:
-------------------------------------------------------------------------------
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn.preprocessing import PolynomialFeatures
# 数据是否需要标准化
scale = False
# 载入数据
data = np.genfromtxt(r"LR-testSet2.txt", delimiter=",")
x_data = data[:, :-1]
y_data = data[:, -1, np.newaxis]
#为了画这个散点图
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
#切分不同类型的数据
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append(x_data[i, 1])
else:
x1.append(x_data[i, 0])
y1.append(x_data[i, 1])
#画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
plot()
plt.show()
#定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=3)
#特征处理
x_poly = poly_reg.fit_transform(x_data)
#逻辑回归的函数
def sigmoid(x):
return 1.0/(1+np.exp(-x))
#逻辑回归的代价函数
def cost(xMat, yMat, ws):
left = np.multiply(yMat, np.log(sigmoid(xMat*ws))) #multiply()是对于矩阵元素的位置进行相乘(矩阵的形状必须一模一样)
right = np.multiply(1-yMat, np.log(1-sigmoid(xMat*ws)))
return np.sum(left + right)/-(len(xMat))
def gradAscent(xArr, yArr):
if scale == True:
xArr = preprocessing.scale(xArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr)
lr = 0.03 #学习率
epochs = 50000 #迭代周期
costList = [] #保存cost的值
#计算数据行列数
#行代表数据个数,列代表权值个数
m, n = np.shape(xMat)
#初始化权值矩阵
ws = np.mat(np.ones((n, 1)))
for i in range(epochs+1):
#xMat和weights矩阵相乘
h = sigmoid(xMat*ws)
#计算误差
ws_grad = xMat.T*(h-yMat)/m
ws = ws - lr*ws_grad
if i%50 == 0:
costList.append(cost(xMat, yMat, ws))
return ws,costList
#训练模型,得到权重和cost值的变化
ws, costList = gradAscent(x_poly, y_data)
print(ws)
#获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
#生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
#ravel与flatten类似,多为数组转一维,flatten不会改变原始数据,ravel会改变
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))
for i in range(len(z)):
if z[i] > 0.5:
z[i] = 1
else:
z[i] = 0
z = z.reshape(xx.shape)
#等高线图
cs = plt.contourf(xx, yy, z)
plot()
plt.show()
#预测
def predict(x_data, ws):
xMat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(x_poly, ws)
print(classification_report(y_data, predictions))
使用sklearn实现非线性逻辑回归:
# -*- coding: utf-8 -*- #
"""
-------------------------------------------------------------------------------
FileName: skl_logistic_regression_method
Author: newlinfeng
Date: 2020/7/28 0028 17:45
Description: 使用sklearn实现非线性逻辑回归
-------------------------------------------------------------------------------
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import make_gaussian_quantiles
from sklearn.preprocessing import PolynomialFeatures
#生成一个二维正态分布,生成的数据按照分位数分成两类,500个样本,2个样本特征
#可以生成两类或多类数据
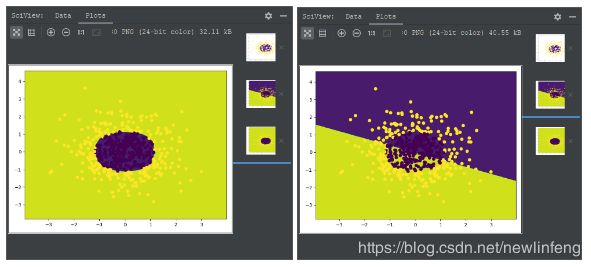
x_data, y_data = make_gaussian_quantiles(n_samples=500, n_features=2, n_classes=2)
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
#获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
#生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
#ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = logistic.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
#等高线图
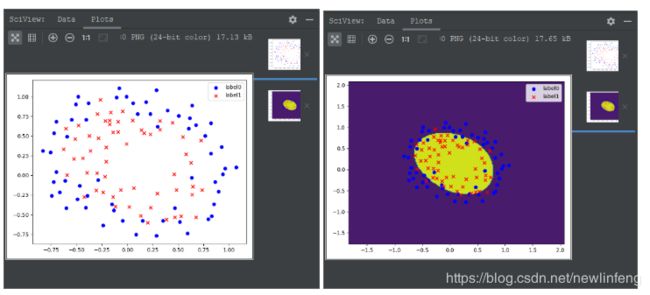
cs = plt.contourf(xx, yy, z)
#样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
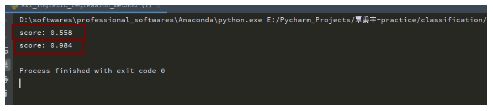
print('score:', logistic.score(x_data, y_data))
#定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=5)
#特征处理
x_poly = poly_reg.fit_transform(x_data)
#定义逻辑回归模型
logistic = linear_model.LogisticRegression()
#训练模型
logistic.fit(x_poly, y_data)
#获取数据值所在的范围
x_min, x_max = x_data[:, 0].min()-1, x_data[:, 0].max()+1
y_min, y_max = x_data[:, 1].min()-1, x_data[:, 1].max()+1
#生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
#ravel和flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]))
z = z.reshape(xx.shape)
#等高线图
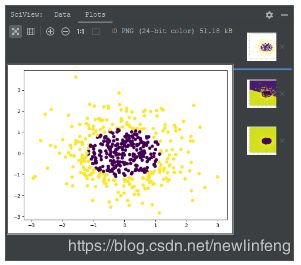
cs = plt.contourf(xx, yy, z)
#样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print('score:', logistic.score(x_poly, y_data))2020-07-31更新