机器学习sklearn（学习笔记6）——SVM支持向量机（未完..）

支持向量机SVM是一种用于分类、回归和异常值检测的监督学习方法。
支持向量机的优点有:

• 适用于高维空间。
• 在原始数据大于样本数的情况下仍然有效。
  -决策函数中(也称为支持向量)使用训练点的子集，它也是储存有效的。
• 通用性:可以为决策函数指定不同的内核函数。提供了通用内核，但也可以指定自定义内核。
  支持向量机的缺点包括:
• 如果特征个数远大于样本个数，在选择核函数时应避免过拟合，正则化项是关键。
• 支持向量机不直接提供概率估计，这些计算比交叉验证消耗多五倍。

SK-LEARN中的支持向量机，支持dense(numpy.ndarray and convertible to that by numpy.asarray)和稀疏矩阵sparse (any scipy.sparse)样本变量的输入。然而，使用SVM去假设稀疏数据，它必须是可以匹配那些数据的。最佳的情况是使用C-ordered numpy.ndarray (dense) 或者 scipy.sparse.csr_matrix (sparse) 在 dtype=float64的情况下。

分类

有以下三种方式SVC、NuSVC和LinearSVC可以展示SVM的数据表现

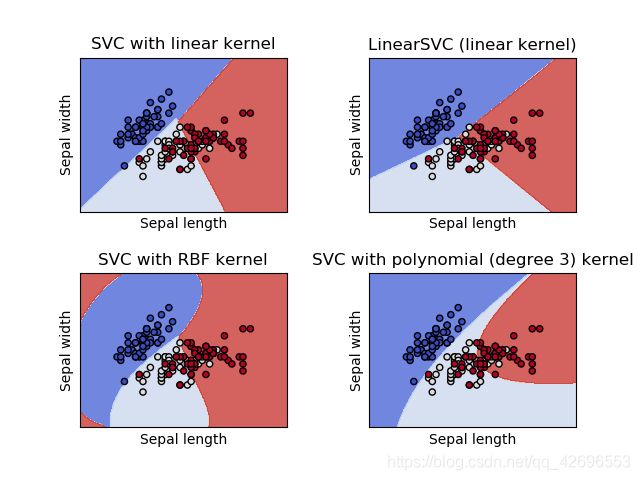
SVC和NuSVC是相似的方法，但是接受的参数集略有不同，并且有不同的数学公式(参见数学公式部分)。另一方面，linear svc是另一种实现支持向量分类的情况下的线性核。注意linear svc不接受关键字kernel，因为这是假定为线性的。它也缺少SVC和NuSVC的一些成员，比如support_。
与其他分类器一样，SVC、NuSVC和LinearSVC将两个数组作为输入:一个数组X大小为[n_samples, n_features]，其中包含训练样本;一个数组y为类标签(字符串或整数)，大小为[n_samples]:

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC(gamma='scale')
>>> clf.fit(X, y)  
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)

拟合后，模型可用于预测新值:

>>> clf.predict([[2., 2.]])
array([1])

SVMs决策函数依赖于训练数据的某个子集，称为支持向量。这些支持向量的一些属性可以在成员support_vectors_、support_和n_support中找到:

>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # get indices of support vectors
>>> clf.support_ 
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_ 
array([1, 1]...)

多层次分类

SVC和NuSVC实现了多类分类的“一对一”方法(Knerr et al.， 1990)。如果n_class是类的数量，则n_class * (n_class - 1) / 2被用来构造分类器，每个分类器训练来自两个类的数据。为了与其他分类器提供一致的接口，decision_function_shape选项允许将“一对一”分类器的结果聚合到shape的决策函数(n_samples, n_classes):

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(gamma='scale', decision_function_shape='ovo')
>>> clf.fit(X, Y) 
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovo', degree=3, gamma='scale', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

另一方面，LinearSVC实现了“one-vs-the-rest”多类策略，从而训练了n_class模型。如果只有两个类，则只训练一个模型:

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y) 
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0)
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

注意，LinearSVC还使用multi_class='crammer_singer’选项实现了另一种多类M策略，也被称为多类SVM。这种方法是一致的，但对于one-vs-rest分类则不正确。在实践中，one-vs-rest分类通常是首选的，因为结果基本相似，但是运行时间明显更少。
对于“one-vs-rest”LinearSVC，属性coef_和intercept_分别具有[n_class, n_features]和[n_class]的独立的形状。系数的每一行对应于的许多“one-vs-rest”分类器中的一个n_class，拦截器也是类似的，按“one”类的顺序排列。
在“one-vs-one”SVC中，属性的布局稍微复杂一些。在具有线性内核的情况下，coef_和intercept_属性的形状分别为[n_class * (n_class - 1) / 2, n_features]和[n_class * (n_class - 1) / 2]。这类似于上面描述的LinearSVC的布局，每一行对应一个二进制分类器。类0到n的顺序是“0 vs 1”、“0 vs 2”、……“0 vs n”、“1 vs 2”、“1 vs 3”、“1 vs n”……“n - 1 vs n”。
dual_coef_的形状是[n_class-1, n_SV]，布局有点难把握。列对应于任何n_class * (n_class - 1) / 2“one-vs- 1”分类器中涉及的支持向量。每个支持向量都用于n_class - 1分类器。每一行中的n_class - 1项对应于这些分类器的对偶系数。
这一点可以用一个例子来说明:
考虑一个三类问题，其中类0有三个支持向量v₀⁰、v₀¹、v₀²，类1和类2分别有两个支持向量v₁⁰、v₁¹和v₂⁰、v₂¹。对于每个支持向量v_i^j，有两个对偶系数。我们叫支持向量的系数v_i^j分类器类之间我和kα_i,k^j。然后dual_coef_看起来是这样的:

分数和概率

SVC和NuSVC的decision_function方法为每个示例给出每个类的得分(或者在二进制情况下，每个示例给出一个得分)。当构造函数选项概率设置为True时，将启用类成员概率估计值(来自predict_proba和predict_log_proba方法)。在二进制情况下，使用Platt scale(支持向量机得分的逻辑回归)对概率进行校准，并通过对训练数据的额外交叉验证进行拟合。在多类情况下，这是按照Wu等人(2004)的方法扩展的。
不用说，对于大型数据集来说，Platt伸缩中涉及的交叉验证是一项昂贵的操作。此外，概率估计可能与得分不一致，因为得分的“argmax”可能不是概率的argmax。(例如,在二元分类,样本可能被预测标记为属于某个类的概率<根据predict_proba½。)普拉特的方法也有理论问题。如果需要信心评分，但这些评分不一定是概率，那么建议设置probability=False并使用decision_function而不是predict_proba。

不平衡的问题

在需要对某些类或某些个别示例给予更多重视的问题中，可以使用关键字class_weight和sample_weight。
SVC(而不是NuSVC)在fit方法中实现关键字class_weight。它是一个形式为{class_label: value}的字典，其中value是一个浮点数> 0，它将class_label类的参数C设置为C * value。

SVC、NuSVC、SVR、NuSVR和OneClassSVM也通过关键字sample_weight对方法中的各个样本进行拟合，实现了对各个样本的权值。与class_weight类似，它们将第i个示例的参数C设置为C * sample_weight[i]

回归

支持向量分类方法可以推广到回归问题的求解。这种方法称为支持向量回归。
支持向量分类(如上所述)生成的模型只依赖于训练数据的子集，因为构建模型的成本函数并不关心超出边界的训练点。类似地，支持向量回归生成的模型只依赖于训练数据的一个子集，因为用于构建模型的成本函数忽略了任何接近于模型预测的训练数据。
支持向量回归有三种不同的实现:SVR、NuSVR和LinearSVR。LinearSVR提供了比SVR更快的实现，但只考虑线性内核，而NuSVR实现的公式与SVR和LinearSVR略有不同。有关详细信息，请参阅实现细节。
与分类类一样，fit方法将取X, y作为参数向量，只是在这种情况下，y应该是浮点值而不是整数值:

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = svm.SVR()
>>> clf.fit(X, y) 
SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1,
    gamma='auto_deprecated', kernel='rbf', max_iter=-1, shrinking=True,
    tol=0.001, verbose=False)
>>> clf.predict([[1, 1]])
array([1.5])

密度估计，异常检验

类OneClassSVM实现了一个用于离群点检测的单类SVM。
有关OneClassSVM的描述和使用，请参见新奇性和异常值检测。

复杂性

支持向量机是一种功能强大的工具，但是它们的计算和存储需求随着训练向量的数量的增加而迅速增加。支持向量机的核心是一个二次规划问题(QP)，它将支持向量从训练数据中分离出来。这个基于libsvm的实现所使用的QP求解器在O(n_features×n²_samples)和O(n_features×n³_samples)之间进行伸缩，这取决于实际使用libsvm缓存的效率(依赖于数据集)。如果数据非常稀疏，n_features应该被样本向量中非零特征的平均数量所代替。
还需要注意的是，对于线性情况，liblinear实现在linear SVC中使用的算法比基于libsvm的SVC实现要有效得多，并且几乎可以线性扩展到数百万个样本和/或特性。

核函数

The kernel function can be any of the following:

不同的内核在初始化时由关键字kernel指定:

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

定制的内核

你可以通过定义自己的内核，将内核作为python函数或通过预计算Gram矩阵来。
带有自定义内核的分类器与任何其他分类器的行为相同，除了:
字段support_vectors_现在是空的，只有支持向量的索引存储在support_中
存储fit()方法中第一个参数的引用(而不是副本)，以便将来引用。如果该数组在使用fit()和predict()之间发生变化，您将得到意想不到的结果。

使用Python函数作为内核

您还可以通过将函数传递给构造函数中的关键字kernel来使用自己定义的内核。
内核必须接受两个形状矩阵(n_samples_1, n_features)， (n_samples_2, n_features)作为参数，并返回一个形状的内核矩阵(n_samples_1, n_samples_2)。
下面的代码定义了一个线性内核，并创建了一个分类器实例，将使用该内核:

>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
...     return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)

使用Gram矩阵

设置kernel=‘precomputed’，在适合的方法中通过Gram矩阵代替X。此时，必须提供所有训练向量与测试向量之间的核值。

>>> import numpy as np
>>> from sklearn import svm
>>> X = np.array([[0, 0], [1, 1]])
>>> y = [0, 1]
>>> clf = svm.SVC(kernel='precomputed')
>>> # linear kernel computation
>>> gram = np.dot(X, X.T)
>>> clf.fit(gram, y) 
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='precomputed', max_iter=-1, probability=False,
    random_state=None, shrinking=True, tol=0.001, verbose=False)
>>> # predict on training examples
>>> clf.predict(gram)
array([0, 1])