Codeforces Round #641 (Div. 2) May/12/2020 20:35UTC+8
Codeforces Round #641 Div. 2
- A. Orac and Factors(找最小质因数)
- B. Orac and Models(最长上升子序列)
- C. Orac and LCM(GCD和LCM的应用)
- D. Orac and Medians(思维)
- E. Orac and Game of Life
比赛链接 https://codeforces.com/contest/1350
比赛记录 https://blog.csdn.net/cheng__yu_/article/details/105395197
A. Orac and Factors(找最小质因数)
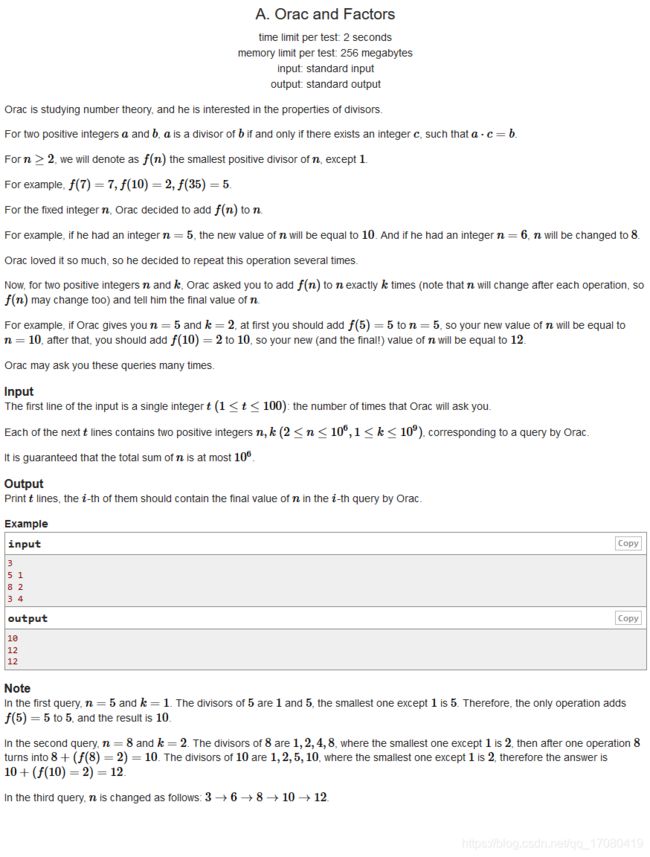
题意:求 k k k 次 n + f ( n ) n + f(n) n+f(n) 。 f ( n ) f(n) f(n)为 n n n 除 1 以外的最小因子
思路:除了第一次以外全都是 +2
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e5+5,maxm=1e5+5;
const int inf=0x7f7f7f7f;
int t;
ll n,k;
ll check(ll n)
{
for(ll i=2;i<=n;++i)
{
if(n%i==0)
return i;
}
}
int main()
{
cin>>t;
while(t--)
{
cin>>n>>k;
ll x=check(n);
ll ans=n+x;
ans=n+x+(k-1)*2;
cout<<ans<<"\n";
}
return 0;
}
B. Orac and Models(最长上升子序列)
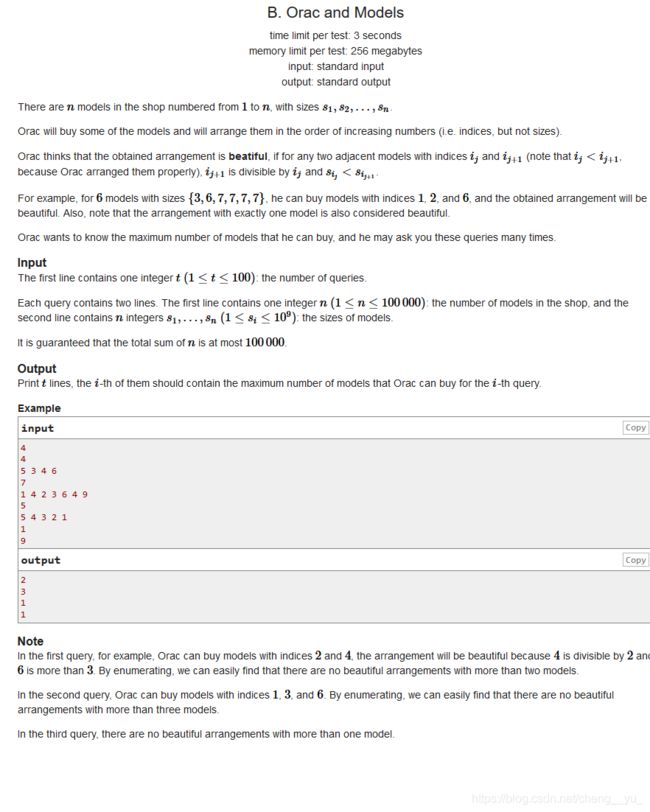
题意:选择一个最长的序列,索引为倍数,元素值不断递增。问最长的长度是多少
思路:现在想想不就是最长上升子序列吗?只不过对索引作了限制。枚举倍数更新, d p [ i ] dp[i] dp[i] 表示以 s i s_i si 结尾的最长上升子序列
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10,maxm=1e5+5;
const int inf=0x7f7f7f7f;
int t,n,s[maxn];
ll dp[maxn];
int main()
{
cin>>t;
while(t--)
{
cin>>n;
for(int i=1;i<=n;++i)
cin>>s[i],dp[i]=1;
for(int i=1;i<=n;++i)
for(int j=2*i;j<=n;j+=i)
if(s[j]>s[i])
dp[j]=max(dp[j],dp[i]+1);
cout<<*max_element(dp+1,dp+1+n)<<"\n";
}
return 0;
}
C. Orac and LCM(GCD和LCM的应用)

题意:求所有最小公倍数的最大公约数
思路:其实就是求 a 数组中每个出现过的素数 第二小 的次数。因为最小公倍数相当于对素数的次数取一个最大,最大公约数就是对素数的次数取一个最小。先取最大,再取最小,就相当于取每个素数第二小的次数的幂
- 对每个 a i a_i ai 分解素因子,统计每个素因子出现的次数,放到vector里面取第二小
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10,maxm=1e5+5;
const int inf=0x7f7f7f7f;
int n,a[maxn];
map<int,vector<int> > m;
const int N=2e5;
int prime[N+10],visit[N+10],cnt;
void init()
{
cnt=0;
for(int i=2;i<=N;++i)
{
if(!visit[i])
prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<=N;++j)
{
visit[i*prime[j]]=1;
if(i%prime[j]==0)
break;
}
}
}
bool isprime(ll x)
{
for(int i=1;prime[i]*prime[i]<=x;++i)
if(x%prime[i]==0)
return false;
return true;
}
void calc(int n)
{
for(int i=1;prime[i]*prime[i]<=n;i++)
{
if(n%prime[i]==0)
{
int res=0;
while(n%prime[i]==0)
n/=prime[i],res++;
m[prime[i]].push_back(res);
}
}
if(n>1)
m[n].push_back(1);
}
ll qpow(ll base,ll n)
{
ll res=1;
while(n)
{
if(n&1)
res=res*base;
base=base*base;
n>>=1;
}
return res;
}
int main()
{
init();
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
for(int i=1;i<=n;++i)
{
if(isprime(a[i]))
m[a[i]].push_back(1);
else
calc(a[i]);
}
ll aa=1;
for(auto it : m)
{
auto pp=it.first;
auto vec=it.second;
sort(vec.begin(),vec.end());
if(vec.size()==n)
aa*=qpow(pp,vec[1]);
else if(vec.size()==n-1)
aa*=qpow(pp,vec[0]);
}
cout<<aa<<"\n";
return 0;
}
D. Orac and Medians(思维)
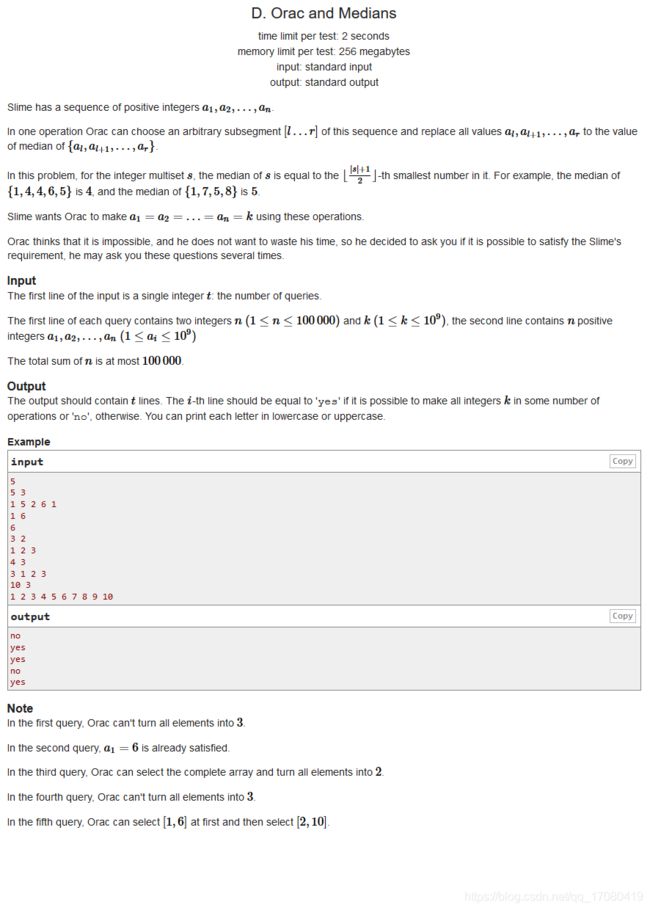
题意:选择数组的任意一段 [ l , r ] [l,r] [l,r] 替换成这一段的中位数,可以替换任意次。问最终能不能把数组全都替换成 k
思路:大于 k 的设为 2,等于 k 的设为 1 ,小于 k 的设为 0 ,只需要判断连续三个数有没有两个大于 1 的
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10,maxm=1e5+5;
const int inf=0x7f7f7f7f;
int t,n,k,a[maxn];
bool solve()
{
bool ok=false;
cin>>n>>k;
for(int i=1;i<=n;++i)
{
cin>>a[i];
if(a[i]==k) ok=true;
if(a[i]>=k) a[i]=1;
else a[i]=0;
}
if(!ok) return false;
if(n==1) return true;
for(int i=1;i<=n;++i)
for(int j=i+1;j<=n&&j-i<=2;++j)
if(a[i]&&a[j])
return true;
return false;
}
int main()
{
cin>>t;
while(t--)
{
puts(solve()?"yes":"no");
}
return 0;
}
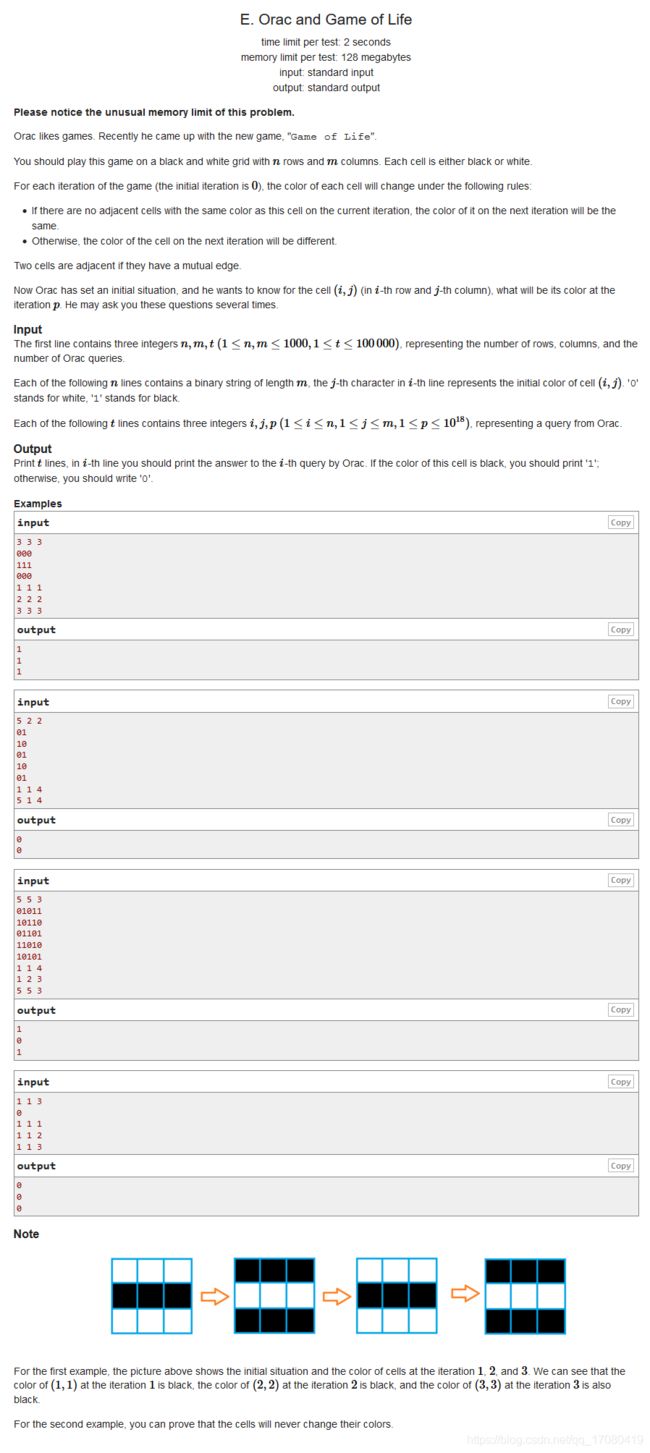
E. Orac and Game of Life
题意:给定一个 n × m n \times m n×m 的棋盘上面有黑白两种颜色的格子。如果一个格子的相邻的格子中,有与它相同颜色的格子。那么在下一次迭代中,它可以和周围相同的颜色的格子一起翻转颜色。给定 t t t 个询问,问位置 ( i , j ) ( i , j ) (i,j)的元素在第 p p p 次迭代后的颜色是什么
思路:
- 可以仔细思考一下迭代的过程:从有颜色相同的点开始不断往外蔓延同化其他不同颜色的点。然后继续往外扩展,直到一个稳定的状态,颜色只有奇偶的变化
- 可以设 d i s [ i ] [ j ] dis[i][j] dis[i][j] 为当前点开始迭代的时间,那么就相当于从 0 开始 一层一层往外搜。bfs整个图搜出每个点的dis即可
#include <bits/stdc++.h>
#define fi first
#define se second
#define ll long long
using namespace std;
const int maxn=1000+10,inf=1e9+7;
int n,m,t;
int dis[maxn][maxn];
int grid[maxn][maxn];
char g[maxn];
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
bool check(int x,int y)
{
for(int i=0;i<=3;++i)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&grid[x][y]==grid[nx][ny])
return true;
}
return false;
}
void bfs()
{
queue<pair<int,int> >q;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if(check(i,j))
q.push({i,j}),dis[i][j]=0;
while(!q.empty())
{
auto t=q.front();
q.pop();
for(int i=0;i<=3;++i)
{
int nx=t.fi+dx[i];
int ny=t.se+dy[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m)
{
if(dis[nx][ny]>dis[t.fi][t.se]+1)
{
dis[nx][ny]=dis[t.fi][t.se]+1;
q.push({nx,ny});
}
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<=n;++i)
{
scanf("%s",g+1);
for(int j=1;j<=m;++j)
grid[i][j]=g[j]-'0',dis[i][j]=inf;
}
bfs();
while(t--)
{
int i,j;
ll p;
scanf("%d%d%lld",&i,&j,&p);
if(dis[i][j]==inf) printf("%d\n",grid[i][j]);
else
{
if(p<=dis[i][j]) printf("%d\n",grid[i][j]);
else printf("%d\n",grid[i][j]^(p-dis[i][j]&1));
}
}
return 0;
}