【带权并查集 He 种类并查集 详详详详详详详hhh】经典例题

POJ 1182 食物链

---

带权并查集

• 在普通并查集的基础上增加了权值，表示结点与其父亲结点之间的某种关系。路径压缩时，关系更新为结点与其祖先的关系。

定义结构体 $animal[u]\{self,fa,relation\}$，意义：结点 $u$ 的标号，结点 $u$ 父亲的标号，结点 $u$ 和它父亲之间的关系

对于这道题，我们可以定义权值的域为{0, 1, 2}，分别表示

• 0：结点u和它的父亲属于同类
• 1：结点u的父亲吃它
• 2：结点u吃它的父亲

我们还可以发现，输入的判断语句：d, x, y，当d=1时，d-1=0刚好是定义的同类；当d=2时，d-1=1刚好是定义的x吃y

如何路径压缩？

我们假设x，fa，grandfa分别为自己，父亲，爷爷

有：$relation[爷爷,x]=(relation[父亲,x]+relation[爷爷,父亲])\%3$

• 穷举验证：

relation[父亲,x]	relation[爷爷,父亲]	relation[爷爷,x]
0	0	0
0	1	1
1	0	1
1	1	2
0	2	2
2	0	2
1	2	0
2	1	0

注意!!:一定要确保父亲的relation是对的，才能更新自己的

int find(node &x)
{
    if(x.self == x.fa) return x.self;
    int fa = x.fa;
    x.fa = find(animal[x.fa]); //得保证父亲的relation是正确的才能更新自己的
    x.relation = (x.relation + animal[fa].relation) % 3;
    return x.fa;
}

如何合并？

将x和y所在的集合合并，我们可以很容易知道 $animal[fy].fa=fx;$ 但是 $fy$ 和 $fx$ 之间的关系怎么确定呢？

如下图：

我们已知：
$①=relation[fx,x]=animal[x].relation$
$②=relation[x,y]=d-1$
$④=relation[fy,y]=animal[y].relation$
$③=3-④$
穷举验证③的正确性：

relation[父亲,x]	relation[x,父亲]
0	0
1	2
2	1

所以，$①+②+③=relation[fx,fy]=animal[fy].relation$

即：$animal[fy].relation=(animal[x].relation+d-1+3-animal[y].relation)$

void Merge(int x, int y, int fx, int fy, int d) //将集合y合并到集合x
{
    animal[fy].fa = fx;
    animal[fy].relation = (animal[x].relation + d - 1 + 3 - animal[y].relation) % 3;
}

解题思路

• 若给定的 $x、y$ 在范围外，那么一定是假话
• 如果 $x、y$ 所在的集合不是一个，那么就是真话，将两个集合进行合并
• 如果 $x、y$ 在同一个集合中【同一个集合中的结点都是连接在根结点的】

1. 如果 $d==1$，那么判断 $animal[x].relation==animal[y].relation?$ 如果不同，说明两个结点和根结点的关系不同，即两个结点不同类：假话
2. 如果 $d==2$，那么判断 $relation[x,y]=(3-animal[x].relation+animal[y].relation)\%3==1?$ 如果 $relation[x,y]\ne 1$ 那么 $x$ 吃 $y$ 是假话
   （：这里的 $(3-animal[x].relation)$ 就是根结点相对于 $x$ 的关系。跟上图:边③的关系道理一样~

---

写完撒花~，花花花花！

#include 
#include 
using namespace std;
typedef long long ll;

int read()
{
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -f; c = getchar(); }
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

const int maxN = 50004;

int n, k, ans;
struct node{
    int self, fa, relation;
}animal[maxN];

void init()
{
    for(int i = 0; i <= n; ++ i )
        animal[i] = node{i, i, 0};
}

int find(node &x)
{
    if(x.self == x.fa) return x.self;
    int fa = x.fa;
    x.fa = find(animal[x.fa]); //得保证父亲的relation是正确的才能更新自己的
    x.relation = (x.relation + animal[fa].relation) % 3;
    return x.fa;
}

void Merge(int x, int y, int fx, int fy, int d) //将集合y合并到集合x
{
    animal[fy].fa = fx;
    animal[fy].relation = (animal[x].relation + d - 1 + 3 - animal[y].relation) % 3;
}

int main()
{
    n = read(); k = read();
    init();
    for(int i = 0; i < k; ++ i )
    {
        int d, x, y;
        d = read(); x = read(); y = read();
        if(x <= 0 || x > n || y <= 0 || y > n)
            ++ ans;
        else
        {
            int fx = find(animal[x]);
            int fy = find(animal[y]);
            if(fx != fy)
                Merge(x, y, fx, fy, d);
            else if(d == 1) //在同一个集合中，判断是不是同类
            {
                if(animal[x].relation != animal[y].relation)
                    ++ans;
            }
            else if(d == 2) //在同一个集合中，判断是不是x吃y，也就是y关于x的relation是不是1
            {
                if((3 - animal[x].relation + animal[y].relation) % 3 != 1)
                    ++ans;
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

---

---

种类并查集

元素分为不同种类的并查集，可以转化为带权并查集解决，就像上面的解法~

but!!

种类并查集也有自己的解法：如果有$n$个种类，在普通并查集的基础上，将原并查集扩展 $n$ 倍。一共有 $n$ 个域。

---

比如该题，我们一共有三个种类，也就有三个域。关系如下图：

如何表示这三个域？

$A：[1,n]$
$B：[n+1,2n]$
$C：[2n+1,3n]$

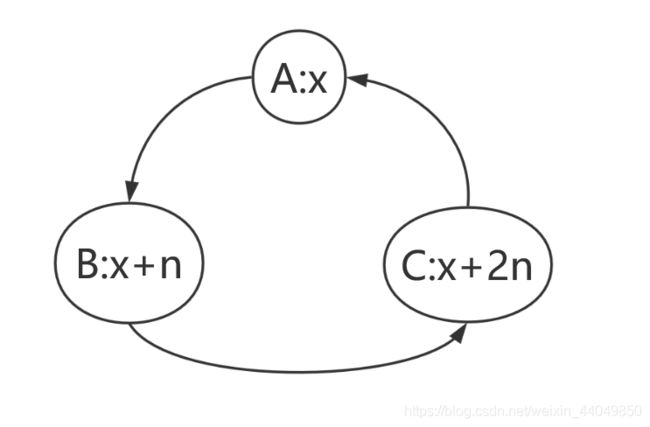
一只动物x，在三个域中的表示：$A:x;B:x+n;C:x+2n$，三者之间也分别有着所在集合间的关系。
也就是 $x$ 吃 $x+n$， $x+n$ 吃 $x+2n$，$x+2n$ 吃 $n$

所以，如果 $1xy$ 即判断 $x、y$ 是不是同类，那么我们首先需要判断：

1. 是不是有 $x$ 吃 $y$，即Same(x+n, y) ？
2. 是不是有 $y$ 吃 $x$，即Same(y+n, x) ？

• 如果都没有，说明 $x、y$ 是同类，那么合并 $(x,y)(x+n,y+n)(x+2n,y+2n)$

如果 $2xy$ 即判断 $x$ 是不是吃 $y$，那么我们首先需要判断：

1. 是不是有 $y$ 吃 $x$，即Same(y+n, x) ？
2. 是不是有l $x、y$ 是同类，即Same(x,y) ？

• 如果都没有，说明 $x$ 吃 $y$，那么合并 $(x+n,y)(x+2n,y+n)(x,y+2n)$

最先写的种类并查集博客

写完写完写完！撒花花~~

---

#include 
#include 
using namespace std;
typedef long long ll;

int read()
{
    int x = 0, f = 1; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -f; c = getchar(); }
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar(); }
    return x * f;
}

const int maxN = 50004;

int n, k, ans;
int root[maxN * 3];
int Find(int x) { return root[x] == x ? x : root[x] = Find(root[x]); }
bool Same(int x, int y) { return Find(x) == Find(y); }
void Merge(int x, int y) { x = Find(x); y = Find(y); if(x != y) root[y] = x; }

void init()
{
    for(int i = 0; i <= n*3; ++ i )
        root[i] = i;
}

int main()
{
    n = read(); k = read();
    init();
    for(int i = 0; i < k; ++ i )
    {
        int d, x, y; d = read(); x = read(); y = read();
        if(x <= 0 || x > n || y <= 0 || y > n)
            ++ans;
        else
        {
            if(d == 1) //判断xy是否同类
            {
                if(Same(x + n, y) || Same(x + 2 * n, y)) //x吃y //y吃x
                    ++ ans;
                else
                {
                    Merge(x, y);
                    Merge(x + n, y + n);
                    Merge(x + 2 * n, y + 2 * n);
                }
            }
            else if(d == 2) //判断x是否吃y
            {
                if(Same(x, y) || Same(x + 2 * n, y)) //xy同类 //y吃x
                    ++ ans;
                else
                {
                    Merge(x + n, y);
                    Merge(x + 2 * n, y + n);
                    Merge(x, y + 2 * n);
                }
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

本篇博客完结啦啦啦~撒花撒花撒花