opencv 距离变换

二值图像距离变换的概念由Rosenfeld和Pfaltz于1966年在论文中提出，目前广泛应用于计算机图形学，目标识别及GIS空间分析等领域，其主要思想是通过表识空间点(目标点与背景点)距离的过程，就是通过使用两遍扫描光栅算法可以快速计算一个图像中非零像素点到最近的零像素点的距离，也就是到所有零像素点的最短距离，最终将二值图像转换为灰度图像。

距离变换按照距离的类型可以分为欧式距离变换(Eudlidean Distance Transfrom)和非欧式距离变换两种，其中，非欧式距离变换又包括棋盘距离变换(Chessboard Distance Transform)，城市街区距离变换(Cityblock Distance Transform)，倒角距离变换(Chamfer Distance Transform)等；

距离变换的主要过程：

假设一幅二值图像I，包含一个连通区域S，其中有目标集O和背景集B，距离图为D，则距离变换的定义如下：

D(p)=Min(disf(p,q))p∈O,q∈B

具体步骤如下：

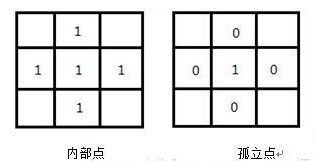
1. 将图像中的目标像素点分类，分为内部点，外部点和孤立点。以中心像素的四邻域为例，如果中心像素为目标像素(值为1)且四邻域都为目标像素(值为1)，则该点为内部点。如果该中心像素为目标像素，四邻域为背景像素(值为0)，则该中心点为孤立点，如下图所示。除了内部点和孤立点之外的目标区域点为边界点。
   
2. 计算图像中所有的内部点和非内部点，点集分别为S1，S2。
3. 对于S1中的每一个内部点(x,y)，使用距离公式disf()计算骑在S2中的最小距离，这些最小距离构成集合S3。
4. 计算S3中的最大最小值Max,Min。

5. 对于每一个内部点，转换后的灰度值G计算如下所示：
   

   G(x,y)=255∗(S3(x,y)−Min)/(Max−Min)

6. 对于孤立点保持不变。

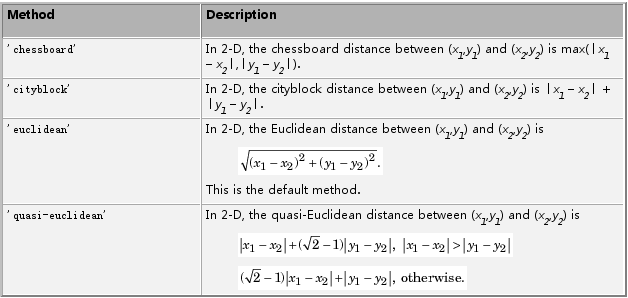
在以上距离变换的过程中，距离函数disf()的选取如果是欧式距离，则该距离变换称为欧式距离变换，依次类推。对于距离的求取，目前主要的距离公式如下：

这里举一个非常直接的例子：
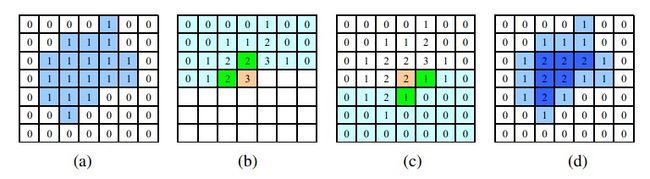
假定我们首先有一个二值的二维数组，如下图(a)所示，现在某个人要从标记为1的坐标到标记为0的坐标，每次只能横向走或纵向走，求这样的最短的路程。
这是非常直接的动规题，实际计算过程中，我们需要先把1变成一个比较大的数，比如255
1. 按照从上到下，从左到右的顺序，依次循环遍历图像I，此过程称为前向循环(b)
状态转移：
disf(x, y) = Min(disf(x - 1, y), disf(x, y - 1), disf(x, y)) + 1
2. 按照从下到上，从右到左的顺序，依次循环遍历图像I，此过程称为后向循环(c)
状态转移：
disf(x, y) = Min(disf(x + 1, y), disf(x, y + 1), disf(x, y)) + 1
3. 最后，我们得到了每个标记为1的坐标到标记为0的坐标的最短距离(d)

好吧，其实这个就是cityBlock的计算方式，在opencv的distTranform函数的参数中表示为CV_DIST_L1。

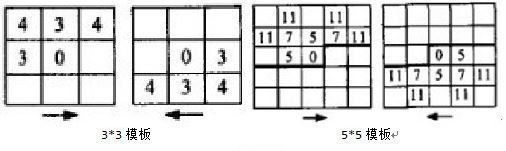
对于欧式距离变换，由于其结果准确，而计算相比非欧式距离变换较为复杂，因此，出现了较多的快速欧式距离变换算法，这里笔者介绍一种基于3*3模板的快速欧式距离变换算法。

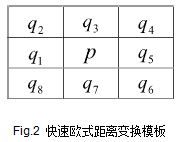
其实跟上面的例子一样，我们也需要前序和后续遍历一遍
只是这里的状态转移发生了变化
前序状态转移：

d0=p

d1 = p1 + disf(p1, p)

d2 = p2 + disf(p2, p)

d3 = p3 + disf(p3, p)

d4 = p4 + disf(p4, p)

则p(x,y)变换后的像素值为：

p = Min(d0,d1,d2,d3,d4);

后续状态转移考虑的是p5, p6, p7, p8, p

对于欧式距离变换算法，相关学者研究了速度更快的倒角距离变换算法，来近似欧式距离变换的效果。具体过程如下：

1. 使用前向模板如图Fig.3中左边3*3模板，对图像从上到下，从左到右进行扫描，模板中心0点对应的像素值如果为0则跳过，如果为1则计算模板中每个元素与其对应的像素值的和，分别为Sum1,Sum2,Sum3,Sum4,Sum5，而中心像素值为这五个和值中的最小值。
2. 使用后向模板如下图中右边的3*3模板，对图像从下到上，从右到左进行扫描，方法同上。
3. 一般我们使用的倒角距离变换模板为3*3和5*5，分别如下图所示。

[参考文献]

1 Rosenfeld A,PfaltzJ.L, Sequential operations in digital pic ture processing. Journal of ACM,1966, 13(4):471-494.

2 Frank Y.Shih,Yi-Ta Wu, Fast Euclidean distance transformation in two scans using a 3*3 neighborhood. Journal of Computer Vision and Image Understanding 2004,195–205.

参考博客：http://blog.csdn.net/trent1985/article/details/18081761