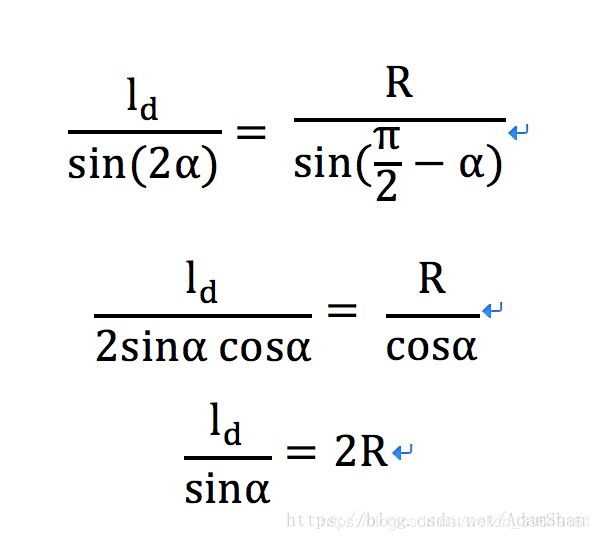无人驾驶轨迹跟踪之纯轨迹跟踪（Pure Pursuit）
无人驾驶轨迹跟踪之纯轨迹跟踪（Pure Pursuit）
- 简要
- 车辆简化模型
- 车辆跟踪模型
- pytho实现纯轨迹跟踪算法
简要
对于无人车来说，规划好的路径通常由一系列路径点构成，这些点包含空间位置信息、姿态信息、速度、加速度等。路径与轨迹区别在于，轨迹包含了时间信息；按照我的理解，路径跟踪只是跟踪一系列路径点，时间长短都没关系，只要跟踪上即可；轨迹跟踪同时包含速度跟踪，与时间序列有关。
目前主流的轨迹跟踪分为两类：
- 基于几何追踪的方法
- 基于模型预测的方法
下面就主要讲一下简单且广泛使用的几何追踪方法。
车辆简化模型
前提假设：将四轮车简化为二轮自行车模型，且假设车辆只在平面上行驶，无滑移，在低速场景中运动。
车辆跟踪模型
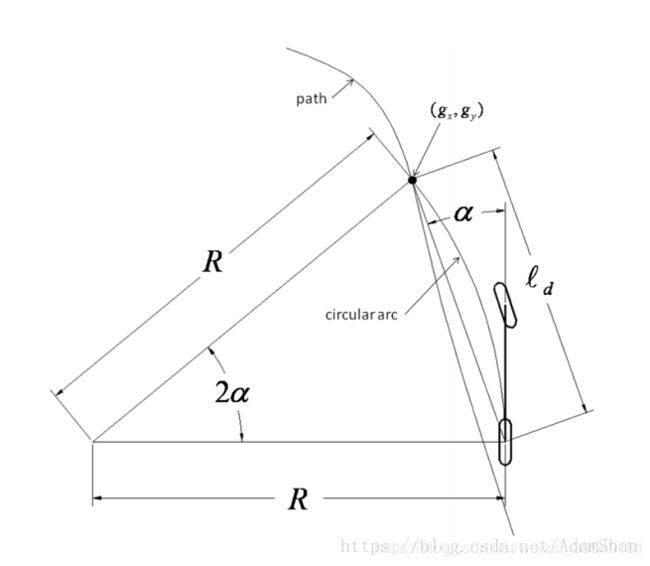
从自行车模型出发，纯跟踪算法以车后轴为切点, 车辆纵向车身为切线, 通过控制前轮转角 ， 使车辆可以沿着一条经过目标路点（goal point）的圆弧行驶，如下图所示：
需要控制车辆的后轴中心点经过要追踪的点，根据正弦定理，得：
结合以上推导，得出纯追踪控制算法控制量表达式：
考虑到本质是横向上的CTE，由上式可知纯追踪控制器其实是一个横向转角的P控制器，这个P控制器受到前视距离的影响很大，如何调整前视距离变成纯追踪算法的关键，通常来说，被认为前视距离是车速的函数，在不同的车速下需要选择不同的前视距离。
一种最常见的调整前视距离的方法就是将前视距离表示成车辆纵向速度的线形函数，即 l=kv，那么前轮的转角公式就变成：
那么纯追踪控制器的调整就变成了调整系数k，通常来说，会使用最大，最小前视距离来约束前视距离，越大的前视距离意味着轨迹的追踪越平滑，小的前视距离会使得追踪更加精确（当然也会带来控制的震荡），下面我们使用Python实现一个简单的纯追踪控制器。
pytho实现纯轨迹跟踪算法
在这个实践中，我们纯追踪控制控制转向角度，使用一个简单的P控制器控制速度，首先我们定义参数数值如下：
import numpy as np
import math
import matplotlib.pyplot as plt
k = 0.1 # 前视距离系数
Lfc = 2.0 # 前视距离
Kp = 1.0 # 速度P控制器系数
dt = 0.1 # 时间间隔，单位：s
L = 2.9 # 车辆轴距，单位：m
在这里我们将最小前视距离设置为2，前视距离关于车速的系数k设置为0.1 ，速度P控制器的比例系数Kp设置为1.0，时间间隔为0.1 秒，车的轴距我们定为2.9米。
定义车辆状态类，在简单的自行车模型中，我们只考虑车辆的当前位置(x,y) ,车辆的偏航角度yaw以及车辆的速度v，为了在软件上模拟，我们定义车辆的状态更新函数来模拟真实车辆的状态更新：
class VehicleState:
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
def update(state, a, delta):
state.x = state.x + state.v * math.cos(state.yaw) * dt
state.y = state.y + state.v * math.sin(state.yaw) * dt
state.yaw = state.yaw + state.v / L * math.tan(delta) * dt
state.v = state.v + a * dt
return state
在这个实践中，我们纵向控制使用一个简单的P控制器，横向控制（即转角控制）我们使用纯追踪控制器，这两个控制器定义如下：
def PControl(target, current):
a = Kp * (target - current)
return a
def pure_pursuit_control(state, cx, cy, pind):
ind = calc_target_index(state, cx, cy)
if pind >= ind:
ind = pind
if ind < len(cx):
tx = cx[ind]
ty = cy[ind]
else:
tx = cx[-1]
ty = cy[-1]
ind = len(cx) - 1
alpha = math.atan2(ty - state.y, tx - state.x) - state.yaw
if state.v < 0: # back
alpha = math.pi - alpha
Lf = k * state.v + Lfc
delta = math.atan2(2.0 * L * math.sin(alpha) / Lf, 1.0)
return delta, ind
定义函数用于搜索最临近的路点：
def calc_target_index(state, cx, cy):
# 搜索最临近的路点
dx = [state.x - icx for icx in cx]
dy = [state.y - icy for icy in cy]
d = [abs(math.sqrt(idx ** 2 + idy ** 2)) for (idx, idy) in zip(dx, dy)]
ind = d.index(min(d))
L = 0.0
Lf = k * state.v + Lfc
while Lf > L and (ind + 1) < len(cx):
dx = cx[ind + 1] - cx[ind]
dy = cx[ind + 1] - cx[ind]
L += math.sqrt(dx ** 2 + dy ** 2)
ind += 1
return ind
主函数:
def main():
# 设置目标路点
cx = np.arange(0, 50, 1)
cy = [math.sin(ix / 5.0) * ix / 2.0 for ix in cx]
target_speed = 10.0 / 3.6 # [m/s]
T = 100.0 # 最大模拟时间
# 设置车辆的出事状态
state = VehicleState(x=-0.0, y=-3.0, yaw=0.0, v=0.0)
lastIndex = len(cx) - 1
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
target_ind = calc_target_index(state, cx, cy)
while T >= time and lastIndex > target_ind:
ai = PControl(target_speed, state.v)
di, target_ind = pure_pursuit_control(state, cx, cy, target_ind)
state = update(state, ai, di)
time = time + dt
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
plt.cla()
plt.plot(cx, cy, ".r", label="course")
plt.plot(x, y, "-b", label="trajectory")
plt.plot(cx[target_ind], cy[target_ind], "go", label="target")
plt.axis("equal")
plt.grid(True)
plt.title("Speed[km/h]:" + str(state.v * 3.6)[:4])
plt.pause(0.001)
if __name__ == '__main__':
main()
运行效果：
