数据结构考试复习
1、表达式a*(b+c)-d的后缀表达式是:abc+*d-
解析:
后缀表达式使用规则:
从左到右遍历表达式的每个数字和符号,遇到的是数字就进栈,遇到的是符号,就将处于栈顶的两个数字出栈,进行运算。
然后将运算结果进栈,直到获得最终结果。
网上找到了另一种简便的方法:
a+b*(c+d/e)
按计算顺序加上括号
(a+(b*(c+(d/e))))
然后将运算符都放到各自的括号外面
(a(b(c(de)/)+)*)+
去掉括号
abcde/+*+附上别人的详细介绍链接
https://blog.csdn.net/c123_sensing/article/details/81904426
2、算法具有的五个重要特性是:
答案:有穷性,确定性,可行性,输入和输出3、平衡二叉树上所有节点的平衡因子只可能是:
答案:-1,0,14、设有二维数组A[6][8],其每个元素占2个字节,数组按行序为主序储存,第一个元素的存储地址为200,则元素A[5][4]的存储地址为:288
解析:
计算方法:200+(5*8+4)*2=288
数组A的体积(即存储量):6*8*2=965、设循环队列中数组的下标范围是0~n-1,其头尾指针分别为f和r,则其元素个数为:(r-f+n)%n
解析:
循环队列头尾指针有两种情况
1. fr : (r+n)-f
两种情况以模运算表示就是(r-f+n)%n 6、假定用于通信的电文仅有7个字母a,b,c,d,e,f,g组成,各个字母在电文中出现的频率分别为4,28,19,5,11,26,7
要求:
(1)以这些频率作为叶子节点的权值构造Huffman树
(2)试为这7个字母设计不等长Huffman编码
解析:
(1)
1.以权值建立一个小跟堆,每次堆中取出最小的k个数,记他们的和为q,将q累加进ans中
2.将q重新放入堆中,在书中我们相当于将权值为q的点作为这k个点的父亲
3.重复步骤1和2,知道堆中只剩一个元素
(2)
设计不等长Huffman编码
沿着Huffman树,从根结点开始,规定往左编码为0,往右编码为1附上别人详细介绍的链接
https://blog.csdn.net/linraise/article/details/1174555
7、链表不具有的特点是()
A 插入、删除不需要移动元素
B 可随机访问任一元素
C 不必事先估计存储空间
D 所需空间与线性长度成正比
答案:
B8、下面说法不正确的是()
A 广义表的表头总是一个广义表
B 广义表的表尾总是一个广义表
C 广义表难以用顺序存储结构
D 广义表可以是一个多层次的结构
答案:
A9、若一颗二叉树有12个度为2的结点,6个度为1的结点,则度为0的结点的个数是()
解析:
二叉树的分支数(度)M和节点数N存在以下关系:
N = M+1;
设度为0的节点有X个;
则:
M = 12*2+6*1;
N = 12+6+x;
18+x = 31;
x=13;10、设有向图G的二元组形式表示为G=(D,R),D={1,2,3,4,5},R={r},r={<1,2>,<2,4>,<4,5>,<1,3>,<3,2>,<3,5>},则给出该图的一种拓扑排序序列
答案:
1,3,2,4,5
解析:
先统计所有节点的入度,对于入度为0的节点就可以分离出来,然后把这个节点指向的节点的入度减一。
一直做改操作,直到所有的节点都被分离出来。
如果最后不存在入度为0的节点,那就说明有环,不存在拓扑排序,也就是很多题目的无解的情况。附上别人详细介绍的链接:
https://blog.csdn.net/qq_41713256/article/details/80805338
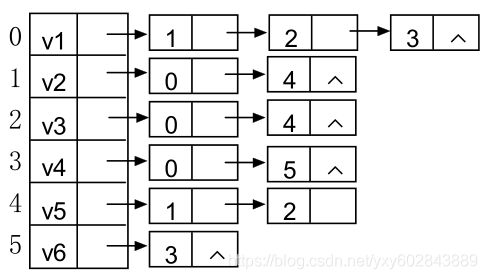
11、已知某无向图中共有六个顶点:V1,V2,V3,V4,V5,V6,按此顺序存储在一位数组中,且其的邻接矩阵为:
0 1 1 1 0 0
1 0 0 0 1 0
1 0 0 0 1 0
1 0 0 0 0 1
0 1 1 0 0 0
0 0 0 1 0 0(1)写出此邻接矩阵对应的邻接表;
(2)写出由V1开始的深度优先遍历的序列;
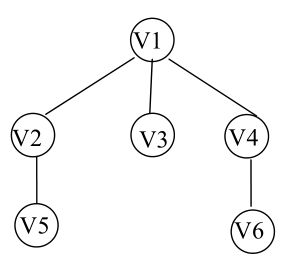
(3)画出由V1开始的广度优先的生成树。
解析
(1)
(2)从V1开始的深度优先遍历的序列:V1,V2,V5,V3,V4,V6
解析:
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。(3)
解析:
广度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次访问v的各个未曾访问过的邻接点,对图进行广度优先遍历;直至图中和v邻接的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行广度优先遍历,直到图中所有顶点均被访问过为止。
12、数据结构从逻辑上划分为四种基本类型:线性结构、()、图状结构和集合。
答案:
树形结构13、设Huffman树中共有99个结点,则该树中有()个叶子结点;若采用二叉链表作为存储结构,则该树中有()个空指针域。
解析:
具有n个叶结点的Huffman树共有结点数为:2*n-1=99,得n=50
用二叉链表存储时每个叶子有2个空指针域,自然二叉链表确实是有100个空指针域14、在程序运行过程中可以扩充的数组是()分配的数组。这种数组在声明它时需要使用数组指针。
答案:
动态15、一棵具有n个结点的二叉树,若它有n0个叶子结点,则该二叉树上度为1的结点n1为(),度为2的结点n2为()
解析:
度为1的结点n1为 n-n0+1
度为2的结点n2为 n+1
对任何一棵二叉树T,如果其终端节点数为n0,度为2的节点数为n2,则n0=n2+1.
设n1为二叉树T中度为1的结点数.因为二叉树中所有结点的度军小于或等于2,所以其结点总数为
n=n0+n1+n2 (1)
再看二叉树中的分支数.除了根结点外,其余结点都有一个分支进入,设B为分支总数,则n=B+1.由于这些分支是由度为1或2的结点射出的,所以B=n1+2n2.于是得
n=n1+2n2+1 (2)
由式(1)(2)得
n0=n2+116、在n个记录的有序顺序表中进行折半查找,最大的比较次数是()
解析:
(log2(n))向下取整+1
17、设单链表中指针p指向结点A,若要删除A之后的结点(若存在),则需要修改指针的操作为()
解析:
p->next=p->next->next
将p的下一个数直接跳过,p后面变为原来的第p+2个数