关于C++各类排序算法与std::sort性能的比较

talk is cheap.直接放代码（C++）。
先定义一个计时的类。

class Time_count//时间计时类，需要#include< ctime>
{
private:
    clock_t start_,end_;
    double duration;//记录时间
public:
    Time_count()
    {
        start_=clock();
    }
    void show_time()
    {
        end_=clock();
        duration = (double)(end_-start_)/CLOCKS_PER_SEC;
        cout< < "spend time "< < duration< < " seconds"< < endl< < endl;
    }
};

然后，计时的时候，实例化一个Time_count类，再通过show_time()成员函数获得时间。这里不细讲。

define LENGTH 10000//排序长度为10000的数组

注意 如果想改变数组长度，只需改变LENGTH大小即可。
开头就这么定义：

 int a[LENGTH+10];
    srand(time(NULL));
    for(int i=0;i< LENGTH;i++)
    {
        a[i]=rand()%10000+1;//随机生成1-10000之间的数字填充进数组
    } 

然后是驱动函数部分：
/*1.以下为插入排序/

 Time_count t1;
    insertion_sort(a);
    cout< < "1.after insertion sort:"< < endl;
    t1.show_time();
    //print(a);
    /**2.以下为冒泡排序*/
    Time_count t2;
    bubble_sort(a);
    cout< < "2.after bubble sort:"< < endl;
    t2.show_time();
    //print(a);
    /**3.以下为选择排序*/
    Time_count t3;
    selection_sort(a);
    cout< < "3.after selection sort:"< < endl;
    t3.show_time();
    //print(a);
    /**4.以下为归并排序*/
    Time_count t4;
    merge_sort(a,0,LENGTH-1);
    cout< < "4.after merge sort:"< < endl;
    t4.show_time();
    //print(a);
    /**5.以下为快速排序*/
    Time_count t5;
    quick_sort(a,0,LENGTH-1);
    cout< < "5.after quick sort:"< < endl;
    t5.show_time();
    //print(a);
    /**6.以下为STLsort排序*/
    Time_count t6;
    STLsort(a);
    cout< < "6.after STLsort:"< < endl;
    t6.show_time();
    //print(a);
    system("pause");

注意：我这个程序一共要比较5种不同的排序算法，以及标准库sort（定义在头文件algorithm里）的算法之间的效率。
冒泡，选择不罗嗦。重点是插入，归并，快排。
插入排序（insertion sort）：算法导论2.1（P17）有详细的说明，而在6（P84），7（P95），8（P107）章中重点对堆排序，快排做了说明。
这些具体的算法抽出时间我再去整理一下。这里就直接贴代码。
//插入排序

void insertion_sort(int *a)
{
    int key;
    int i,j;
    for(j=1;j< LENGTH;j++)
    {
        key=a[j];
        i=j-1;
        while(i>0&&a[i]>key)
        {
            a[i+1]=a[i];
            i--;
        }
        a[i+1]=key;
    }
}
//归并排序(注意！last应为a数组长度-1)
void merge_sort(int *a,int first,int last)
{
    if (first<  last)
    {
 int mid = (first + last) / 2;
merge_sort(a, first, mid);    //左边有序
merge_sort(a, mid + 1, last); //右边有序
//再将二个有序数列合并
    int i = first, j = mid + 1;
            int m = mid,   n = last;
            int k = 0;
            int *temp;
            if((temp=(int*)malloc(LENGTH*sizeof(int)))==0)
            {
                cout< < "fuck you"< < endl;
                exit(1);
            }
            while (i < = m && j < = n)
            {
                if (a[i] < = a[j])
                    temp[k++] = a[i++];
                else
                    temp[k++] = a[j++];
            }
            while (i < = m)
            {
                temp[k++] = a[i++];
            }
            while (j < = n)
            {
                temp[k++] = a[j++];
            }
            for (i = 0; i <  k; i++)
            {
                a[first + i] = temp[i];
            }
}
}



   //快速排序
void quick_sort(int *a, int l, int r)
{
    if (l <  r)
    {//Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = a[l];
        while (i <  j)
        {
            while(i <  j && a[j] >= x) // 从右向左找第一个小于x的数
            {
                j--;
            }
            if(i <  j)
a[i++] = a[j];
            while(i <  j && a[i] <  x) // 从左向右找第一个大于等于x的数
            {
                i++;
            }
            if(i <  j)
a[j--] = a[i];
        }
        a[i] = x;
        quick_sort(a, l, i - 1); // 递归调用
        quick_sort(a, i + 1, r);
    }
} 

最后，打印结果：

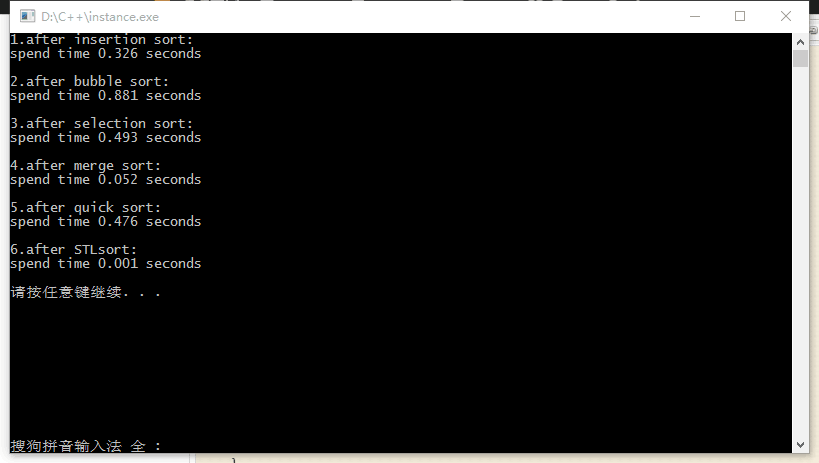
惊讶的发现，快排没那么快（其实原因是快排还有很多改进版本，如随机选择基准数，区间内数据较少时直接用另的方法排序以减小递归深度，而本程序使用的快排却并不是最好的。这里不做过多的讨论）。本地图片，请重新上传而STL的sort函数却相当的快。
那么，如果加大LENGTH的长度呢？比如，#define LENGTH 50000 会怎么样呢？
试试看

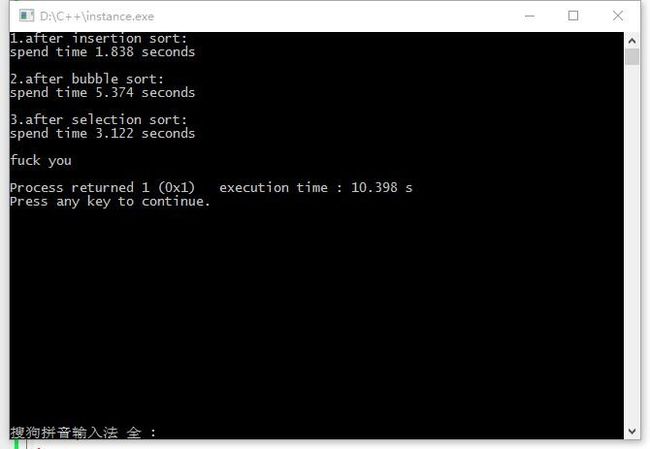
啊哈，调用merge_sort的时候 因为要开过多的空间，导致栈溢出了。
因为quick_sort也是通过空间换时间的算法，所以递归调用时同样会导致栈溢出。
那么，把merge和quick注释掉，看看结果：

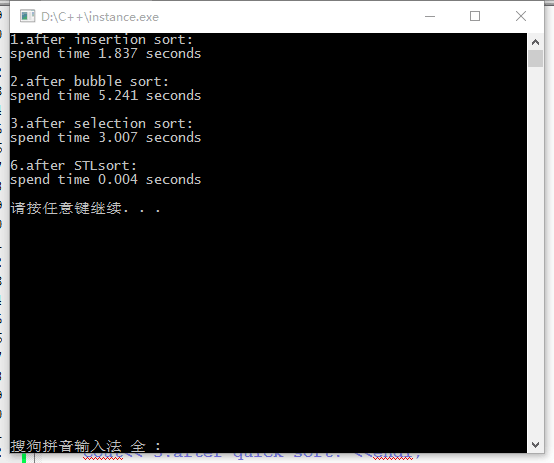
STL的sort函数还是傲视群雄。根本没用多少时间。
为什么标准库的排序函数会这么快？
我们进algorithm标准库看看吧

我们可以看到很多乱七八糟的C++代码。从这个STL函数来看，重载了两个版本的sort函数，第一个接收三个参数，第二个接收两个。因为定义的是模板，因此参数无论传入指针，还是迭代器都是没问题的。第三个参数可以使用一个比较函数，bool cmp(T &a,T &b);之类的，也可以用funtional标准库中的equal_to< Type>、not_equal_to< Type>、greater< Type>、greater_equal< Type>、less< Type>、less_equal< Type>等等进行大小比较，甚至还可以利用C++11的feature自己写个lambda表达式。当然这里不赘述。主要看sort函数的实现原理。
继续f12，跳。

template< class _RanIt,
class _Diff,
class _Pr> inline
void _Sort(_RanIt _First, _RanIt _Last, _Diff _Ideal, _Pr _Pred)
{// order [_First, _Last), using _Pred
_Diff _Count;
for (; _ISORT_MAX <  (_Count = _Last - _First) && 0 <  _Ideal; )
{// divide and conquer by quicksort
pair< _RanIt, _RanIt> _Mid =
_Unguarded_partition(_First, _Last, _Pred);
_Ideal /= 2, _Ideal += _Ideal / 2;// allow 1.5 log2(N) divisions

if (_Mid.first - _First <  _Last - _Mid.second)
{// loop on second half
_Sort(_First, _Mid.first, _Ideal, _Pred);
_First = _Mid.second;
}
else
{// loop on first half
_Sort(_Mid.second, _Last, _Ideal, _Pred);
_Last = _Mid.first;
}
}

if (_ISORT_MAX <  _Count)
{// heap sort if too many divisions
_STD make_heap(_First, _Last, _Pred);
_STD sort_heap(_First, _Last, _Pred);
}
else if (2 < = _Count)
_Insertion_sort(_First, _Last, _Pred);// small
}

template< class _RanIt,
class _Pr> inline
void sort(_RanIt _First, _RanIt _Last, _Pr _Pred)
{// order [_First, _Last), using _Pred
_DEBUG_RANGE(_First, _Last);
_DEBUG_POINTER_IF(2 < = _Last - _First, _Pred);
_Sort(_Unchecked(_First), _Unchecked(_Last), _Last - _First, _Pred);
}

// TEMPLATE FUNCTION sort
template< class _RanIt> inline
void sort(_RanIt _First, _RanIt _Last)
{// order [_First, _Last), using operator< 
_STD sort(_First, _Last, less< >());
}

其实STL的sort函数在数据量大时采用快排，分段递归排序，一旦分段后的数据小于某个值，就改用插入排序。如果递归层次过深，还会改用堆排序。这样就结合了各类算法的所有优点。