算法基础:排序与查找
![]()
1、直接插入排序
1.1、基本思想:
在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的;如此反复循环,直到全部排好顺序。
1.2、实现思路:
INSERTION_SORT(A)
for i = 2 to n
j = i-1
key = A[i]
while j > 0 && A[j] > key
A[j+1] = A[j]
j--
A[j+1] = key1.3、算法实现:
public static int[] insertionSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
for(int i = 1; i < A.length; i++){
int j = i - 1;
int key = A[i];
while(j >= 0 && A[j] > key){
A[j+1] = A[j];
j--;
}
A[j+1] = key;
}
return A;
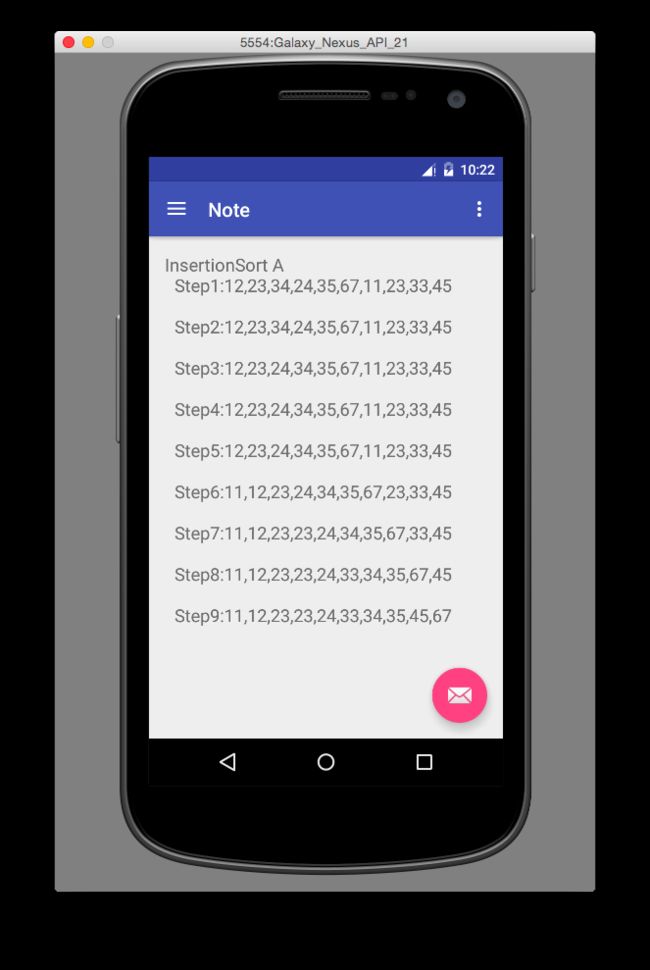
}1.4、算法实例:
1.5、复杂度描述:
将未排序的元素插入到以排序的序列中,如果元素本身都是有序的,那么在最好的情况下排序过程就可以省略只需进行元素插入,时间复杂度为O(n),最坏的情况下则既需排序也需插入,时间复杂度为O(n^2)。
1.6、稳定性描述:
一般插入排序,比较是从有序序列的最后一个元素开始,如果比它大则直接插入在其后面,否则一直往前比;如果找到一个和插入元素相等的,那么就插入到这个相等元素的后面,所以插入排序是稳定的。
2、希尔排序
2.1、基本思想:
算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
2.2、实现思路:
SHELL_SORT(A)
d = ceil(A.length/2)
while d >= 1
SHELL_INSERT_SORT(A, d)
if d/2 >= 1
d = ceil(d/2)
else
d = d/2SHELL_INSERT_SORT(A, d)
for i = d to n
if A[i] < A[i-d]
j = i-d
key = A[i]
while j>=0 && A[j] > key
A[j+d] = A[j]
j -= d
A[j+d] = key2.3、算法实现:
public static int[] shellSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
int d = (int) Math.ceil((double) A.length / 2);
while(d >= 1){
shellInsertSort(A, d);
if(d/2 >= 1){
d = (int) Math.ceil((double) d / 2);
} else{
d = d / 2;
}
}
return A;
}
private static void shellInsertSort(int[] A, int d){
for(int i = d; i < A.length; i++){
if(A[i] < A[i-d]){
int j = i - d;
int key = A[i];
while(j >= 0 && A[j] > key){
A[j+d] = A[j];
j -= d;
}
A[j+d] = key;
}
}
}2.4、算法实例:
2.5、复杂度描述:
希尔排序是改善后的插入排序,最好和最坏的时间复杂度一样,但是由于希尔排序减少了移动和比较次数,平均下来的时间复杂度要远远优于简单的插入排序。
2.6、稳定性描述:
希尔排序是按照不同步长对元素进行插入排序,一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,稳定性就会被破坏,所以希尔排序不稳定。
3、直接选择排序
3.1、基本思想:
在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
3.2、实现思路:
SELECTION_SORT(A)
for i = 1 to n-1
min = i
for j = i+1 to n
if A[min] > A[j]
min = j
swap A[min] <-> A[i]3.3、算法实现:
public static int[] selectionSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
for(int i = 0; i < A.length - 1; i++){
int minIndex = i;
for(int j = i+1; j < A.length; j++){
if(A[minIndex] > A[j]){
minIndex = j;
}
}
//swap A[minIndex],A[i]
int temp = A[minIndex];
A[minIndex] = A[i];
A[i] = temp;
}
return A;
}3.4、算法实例:
3.5、复杂度描述:
不管什么情况下都必须满足双层遍历,故最好和最坏的时间复杂度都为O(n^2).
3.6、稳定性描述:
在某一趟选择中,如果元素A比元素B小,而该元素A又出现在一个和元素B相等的元素后面,那么交换后稳定性就被破坏了,所以选择排序不稳定。
4、堆排序
4.1、基本思想:
堆排序是一种树形选择排序,是对直接选择排序的有效改进。
4.2、实现思路:
HEAP_SORT(A)
BUILD_MAX_HEAP(A)
heapSize = A.length
for i = n to 2
swap A[i] <-> A[heapSize]
heapSize--
MAX_HEAPIFY(A, i)BUILD_MAX_HEAP(A)
for i = floor(n/2) to 1
MAX_HEAPIFY(A, i)MAX_HEAPIFY(A, i)
heapSize = A.lenght
largest = i
if i.left <= heapSize && A[largest] < A[i.left]
largest = i.left
else if i.right <= heapSize && A[largest] < A[i.right]
largest = i.right
if largest != i
swap A[i] <-> A[largest]
MAX_HEAPIFY(A, largest)4.3、算法实现:
public static int[] heapSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
buildMaxHeap(A);
int heapSize = A.length;
for(int i = heapSize-1; i > 0; i--){
int temp = A[i];
A[i] = A[0];
A[0] = temp;
heapAdjust(A, 0, i);
}
return A;
}
private static void buildMaxHeap(int[] A){
for (int i = (A.length -1) / 2 ; i >= 0; --i){
heapAdjust(A, i, A.length);
}
}
private static void heapAdjust(int[] A, int s, int length){
int temp = A[s];
int child = 2*s+1;
while (child < length) {
if(child+1 < length && A[child] < A[child+1]){
child++;
}
if(A[s] < A[child]){
A[s] = A[child];
s = child;
child = 2*s+1;
} else{
break;
}
A[s] = temp;
}
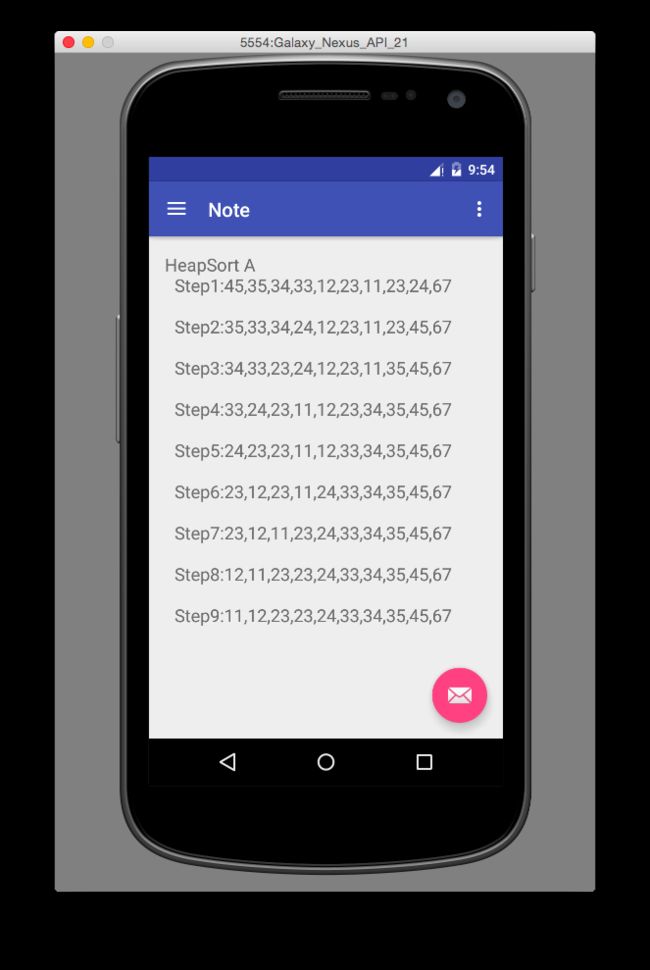
}4.4、算法实例:
4.5、复杂度描述:
堆排序是改善后的选择排序,主要由建立堆和调整堆两部分组成,其中建立堆的复杂度为O(logN),则堆排序的时间复杂度为O(nlogN).
4.6、稳定性描述:
堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n/2-1, n/2-2, …这些父节点选择元素时,有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1个父节点把后面一个相同的元素没有交换,所以堆排序并不稳定。
5、冒泡排序
5.1、基本思想:
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
5.2、实现思路:
BUBBLE_SORT(A)
for i = 1 to n
for j = n to i+1
if A[j] < A[j-1]
swap A[j] <-> A[j-1]5.3、算法实现:
public static int[] bubbleSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
for(int i = 0; i < A.length; i++){
for(int j = A.length-1; j > i; j--){
if(A[j] < A[j-1]){
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
return A;
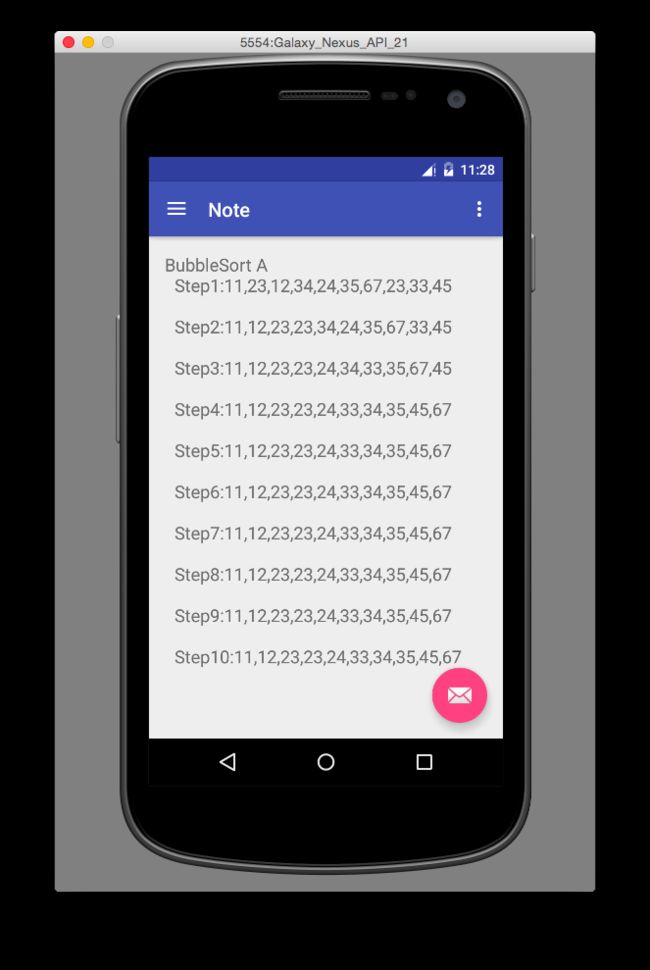
}5.4、算法实例:
5.5、复杂度描述:
如果较小的数在前,较大的数在后,那么最好的情况下冒泡排序是O(n)的常数倍,则复杂度为O(n),最坏的情况下的复杂度为O(n^2).
5.6、稳定性描述:
冒泡排序是相邻的两个元素比较,交换也发生在这两个元素之间,如果两个元素相等,不用交换。所以冒泡排序稳定。
6、快速排序
6.1、基本思想:
选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
6.2、实现思路:
QUICK_SORT(A)
RECURSIVE_QUICK_SORT(A, 1, A.length)RECURSIVE_QUICK_SORT(A, p, q)
if p < q
r = PARTITION(A, p, q)
RECURSIVE_QUICK_SORT(A, p, r-1)
RECURSIVE_QUICK_SORT(A, r+1, q)PARTITION(A, p, q)
pivot = A[p]
while p < q
while p < q && A[q] >= A[p]
--q
swap A[p] <-> A[q]
while p < q && A[q] <= A[p]
++p
swap A[p] <-> A[q]
return q6.3、算法实现:
public static int[] quickSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
recursiveQuickSort(A, 1, A.length);
return A;
}
private static void recursiveQuickSort(int[] A, int p, int q) {
if(p < q){
int r = partition(A, p, q);
recursiveQuickSort(A, p, r-1);
recursiveQuickSort(A, r+1, q);
}
}
private static int partition(int[] A, int p, int q){
int pivot = A[p];
while(p < q){
while(p < q && A[q] >= pivot) --q;
int tempFirst = A[q];
A[q] = A[p];
A[p] = tempFirst;
while(p < q && A[p] <= pivot) ++p;
int tempSecond = A[q];
A[q] = A[p];
A[p] = tempSecond;
}
return p;
}6.4、算法实例:
6.5、复杂度描述:
如果较小的数在前,较大的数在后,那么最好的情况下快速排序的时间复杂度为O(nlogN),最坏的情况下的时间复杂度为O(n^2);快速排序需要选择基准元素进行分段扫描,所以需要部分辅助空间,其空间复杂度为O(nlogN).
6.6、稳定性描述:
在中枢元素和序列中元素A交换的时候,如果前面有与元素A相同的元素,则把前面的元素的稳定性打乱,所以快速排序不稳定。
7、归并排序
7.1、基本思想:
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
7.2、实现思路:
MERGE_SORT(A)
RECURSIVE_MERGE_SORT(A, 1, A.length)
return ARECURSIVE_MERGE_SORT(A, p, q)
if p < q
m = (p + q) / 2
RECURSIVE_MERGE_SORT(A, p, m)
RECURSIVE_MERGE_SORT(A, m+1, q)
MERGE(A, p, m, q)MERGE(A, p, m, q)
create array B[q-p+1]
i = p
j = m + 1
k = 1
while i <= m && j <= q
if A[i] < A[j]
B[k++] = A[i++]
else
B[k++] = A[j++]
while i <= m
B[k++] = A[i++]
while j <= q
B[k++] = A[j++]
for t = 1 to n
A[t+p] = B[t]7.3、算法实现:
public static int[] mergeSort(int[] A){
if(A == null || A.length <= 1){
return A;
}
mergeSort(A, 0, A.length-1);
return A;
}
private static int[] mergeSort(int[] A, int low, int high){
int mid = (low + high) / 2;
if (low < high) {
mergeSort(A, low, mid);
mergeSort(A, mid + 1, high);
merge(A, low, mid, high);
}
return A;
}
private static void merge(int[] A, int low, int mid, int high){
int[] temp = new int[high-low+1];
int i = low;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= high) {
if (A[i] < A[j]) {
temp[k++] = A[i++];
} else {
temp[k++] = A[j++];
}
}
while (i <= mid) {
temp[k++] = A[i++];
}
while (j <= high) {
temp[k++] = A[j++];
}
for (int t = 0; t < temp.length; t++) {
A[t+low] = temp[t];
}
}7.4、算法实例:
7.5、复杂度描述:
归并排序主要在于对有序表的合并,其时间复杂度为O(nlogN),空间复杂度为O(n).
7.6、稳定性描述:
在分解的子列中,有1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不会交换。在序列合并的过程中,如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,所以归并排序也是稳定的。
8、基数排序
8.1、基本思想:
将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
8.2、实现思路:
RADIX_SORT(A, radix, d)
create array B[n] && C[radix]
rate = 1
for i = 1 to d
C.clean
B copy A
for j = 1 to n
key = (B[j] / rate) % radix
C[key]++
for j = 2 to radix
C[j] = C[j] + C[j-1]
for m = n to 1
key = (B[m] / rate) % radix
A[--C[key]] = B[m]
rate *= radix
return A8.3、算法实现:
public static int[] radixSort(int[] A, int radix, int d){
if(A == null || A.length <= 1){
return A;
}
int[] tmp = new int[A.length];
int[] buckets = new int[radix];
for (int i = 0, rate = 1; i < d; i++) {
Arrays.fill(buckets, 0);
System.arraycopy(A, 0, tmp, 0, A.length);
for (int j = 0; j < A.length; j++) {
int subKey = (tmp[j] / rate) % radix;
buckets[subKey]++;
}
for (int j = 1; j < radix; j++) {
buckets[j] = buckets[j] + buckets[j - 1];
}
for (int m = A.length - 1; m >= 0; m--) {
int subKey = (tmp[m] / rate) % radix;
A[--buckets[subKey]] = tmp[m];
}
rate *= radix;
}
return A;
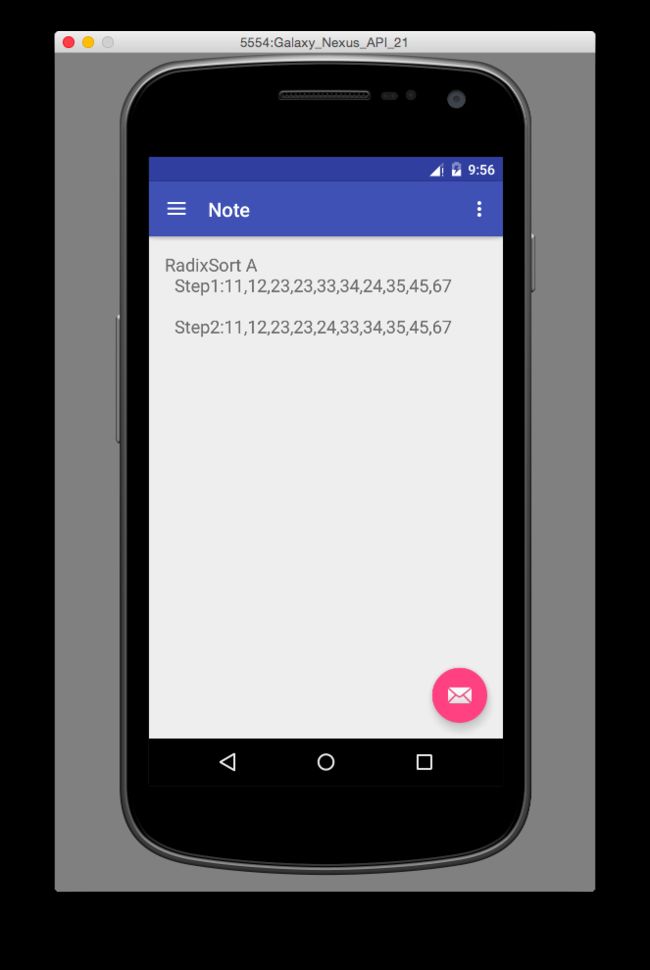
}8.4、算法实例:
8.5、复杂度描述:
基数排序主要在于每个位的排序选择,其复杂度取决于单个部分的排序选择的复杂度。
8.6、稳定性描述:
是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
算法实例源码地址:https://github.com/xiaoyaoyou1212/Algorithm
(注:以上为基本的八大排序算法描述)
9、顺序查找
9.1、基本思想:
顺序查找是在一个已知无(或有序)序队列中找出与给定关键字相同的数的具体位置。原理是让关键字与队列中的数从最后一个开始逐个比较,直到找出与给定关键字相同的数为止,它的缺点是效率低下。
9.2、算法实现:
public static int orderSearch(int[] A,int key){
for(int i = 0; i < A.length; i++){
if(key == A[i]){
return i;
}
}
return -1;
}10、二分查找
10.1、基本思想:
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
10.2、算法实现:
public static int binarySearch(int[] A, int key){
int low = 0;
int high = A.length - 1;
while ((low <= high) && (low < A.length) && (high < A.length)) {
int middle = (high + low) >> 1;
if (key == A[middle]) {
return middle;
} else if (key < A[middle]) {
high = middle - 1;
} else {
low = middle + 1;
}
}
return -1;
}11、索引查找
11.1、基本思想:
索引查找是在索引表和主表(即线性表的索引存储结构)上进行的查找。索引查找的过程是:首先根据给定的索引值K1,在索引表上查找出索引值等于K1的索引项,以确定K1对应的子表在主表中的开始位置和长度,然后再根据给定的关键字K2,在对应的子表中查找出关键字等于K2的元素(结点)。
11.2、算法实现:
public static int indexSearch(int[] A, int key, int indexRule){
if(A == null || A.length <= 0 || indexRule == 0){
return -1;
}
IndexItem item = null;
IndexItem[] indexItems = createIndexList(A, indexRule);
if(indexItems == null || indexItems.length <= 0){
return -1;
}
int index = key / indexRule;
for (int i = 0; i < indexItems.length; i++){
if (indexItems[i].index == index){
item = new IndexItem(index, indexItems[i].start,
indexItems[i].length);
break;
}
}
if (item == null){
return -1;
}
for (int i = item.start; i < item.start + item.length; i++){
if (A[i] == key){
return i;
}
}
return -1;
}
private static IndexItem[] createIndexList(int[] A, int indexRule){
if(A == null || A.length <= 0 || indexRule == 0){
return null;
}
ArrayList indexItemArrayList = new ArrayList<>();
//根据索引规则建立索引表,规则不一,此处省略
for(int i = 0; i < A.length; i++){
//按照索引规则放置原始数据,与生成目录类似
}
IndexItem[] indexItems = (IndexItem[]) indexItemArrayList.toArray();
return indexItems;
}
// 索引项实体
static class IndexItem {
// 对应主表的值
public int index;
// 主表记录区间段的开始位置
public int start;
// 主表记录区间段的长度
public int length;
public IndexItem() {
}
public IndexItem(int index, int start, int length) {
this.index = index;
this.start = start;
this.length = length;
}
} 12、散列查找
基本思想:以每个元素的关键字K为自变量,通过一个函数(称为哈希函数或散列函数)计算出函数值,把这个值(哈希地址或散列地址)解释为一块连续存储空间(即数组空间)的单元地址(即下标),将该元素存储到这个单元中,使用的数组空间是线性表进行散列存储的地址空间,所以被称之为散列表或哈希表(Hash list或Hash table),再通过查找散列表或哈希表来确定元素。
注:散列查询主要在于散列函数的选取及解决地址冲突的方法,由于选择的多样性,这里便不一一详解。