数据结构与算法：排序（分类）

一、分类概述

二、插入分类方法（直接插入、折半插入）

三、交换分类方法（冒泡分类、穿梭分类、快速分类）

四、选择分类方法（简单选择分类、树选择分类、堆分类）

五、归并分类方法（2-路归并分类）

 

一、分类概述

1.排序：它是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。

具体定义为：

假设含n个记录的序列为 { R1, R2, …， Rn } ， 其相应的关键字序列为 { K1, K2, …，Kn }， 这些关键字相互之间可以进行比较，即在它们之间 存在着这样一个关系：Kp1≤Kp2≤…≤Kpn 按此固有关系将记录序列 { R1, R2, …， Rn } 重新排列为 { Rp1, Rp2, …，Rpn } 的过程称作 分类。

2.内部分类和外部分类

（1）内部分类：若整个分类过程不需要访问外存便能完成，则称为内部分类；

（2）外部分类：若参加分类的记录数量很大，整个序列的分类过程不可能在内存中完成，则称其为外部分类。

事实上，由于现在计算机硬件技术发展突飞猛进，想仅凭一个排序就占满整个内存不太现实，即使有这样的排序，我们现在应该也用不到，所以我主要说一下内部分类。

3.内部分类的方法

（1）内部排序的过程是一个逐步扩大记录的有序序列的长度的过程。在排序过程中，参与排序的记录序列中存在两个区域：有序区和无序区，如下图：

（2）使有序区中记录的数目增加一个或几个的一遍操作称为一趟排序。

一种排序方法执行一趟分类的方法是不同的，且一般都由多趟组成（方法不同趟数不同）。

（3）根据分类方法进行一趟的基本操作不同，内部分类方法分为下面几大类：

1）基于“插入”思想的分类方法：执行一趟是将一个元素“插入”到有序序列中仍然有序，使有序部分扩大。这类方法有： 直接插入分类、折半插入分类 、表插入分类、2路插入分类、SHELL分类；

2）基于“交换”思想的分类方法：执行一趟是通过交换“逆序”元素使之到有序序列中，使有序部分扩大。这类方法有： 冒泡分类、、奇偶交换分类、穿梭分类、快速分类；

3）基于“选择”思想的分类方法：执行一趟是通过出当前无序部分的最小元素放到有序序列的后面，使有序部分扩大。这类方法有：简单选择分类、锦标赛（打擂台）分类、堆分类；

4）基于“归并”思想的分类方法：执行一趟是通过归并两个短的有序序列为一个有序序列，使有序部分扩大。这类方法有：2路归并分类、多路归并分类；

5）其他思想的分类方法：计数分类、基数分类。 

（4）内部分类方法的效率问题

①时间效率：比较次数、交换或移动次数（一次交换=三次移动）；

②空间效率：除了存储元素本身所需的空间外，分类过程中需要的空间大小；

（5）分类方法的稳定性

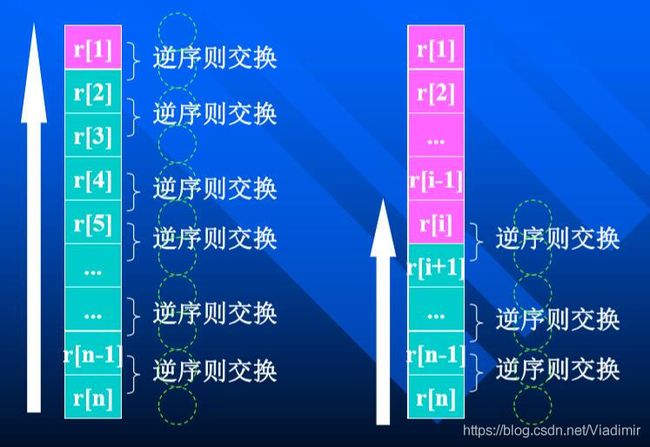
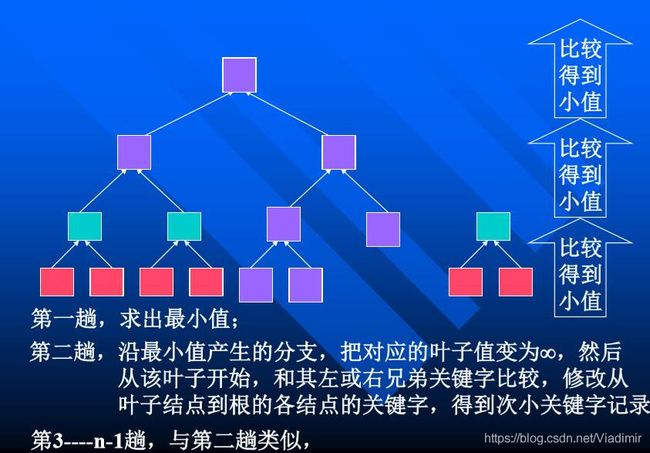
若有两个元素记Ri,Rj，Ki=Kj，(1<=i<=n, 1<=j <= n)，且分类 前Ri在Rj之前(即i

反之，若分类后可能会出现Ri在Rj之后(即i>j)，则称 所用的分类方法是不稳定的。

也就是说，对于内容相等的两个元素（当然，这两个元素关键码不一样），如果排完序（分玩类）后它们俩的相对位置不变，那么称该排序（分类）方法是稳定的，反之，是不稳定的。

（一般普通的分类方法都是稳定的，高效分类方法都是不稳定的。）

 

二、插入分类方法

1.插入分类方法的基本思想

（1）假设待分类记录集合为R1,R2,...Rn，简记为R[1...n]。 插入分类方法由n趟组成，假设要进行第i趟，此时 第1~i-1个记录已经插入排好序，第i趟是将第i个记录 插入到有序序列中，使之仍然有序。

“将记录Ri插入到有序子序列R[1..i-1]中，使记录的 有序序列从R[1..i-1]变为R[1..i]”。即找到Ri的位置并放入该位置。

（2）显然，完成这个“插入”需分三步进行：

1）查找Ri的插入位置j；

2）将R[j..i-1]中的记录后移一个位置； 

3）将将Ri复制到Rj的位置上。

（3）根据查找位置的方法不同、移动记录的方法不同， 插入分类有多种方法： 

1）直接插入分类——查找采用顺序查找方法 ；

2）折半插入分类——查找采用折半查找方法；

3）2-路插入分类——移动有了变化；

4）SHELL分类——提高效率的改进（移动步长变化）；

（4）直接插入分类

1）基本思想

利用顺序查找实现“在R[1..i-1]中查找R[i]的插入位置”的插入排序。

第i趟描述为：

①从Ri-1起向前进行顺序查找,查找位置j，满足： Rj.key<=Ri.key

②对于在查找过程中找到的那些关键字不小于 Ri.key的记录，并在查找的同时实现记录向后移动；

③ 插入到正确位置，Rj:= R0。

2）效率分析：

①最好的情况（关键字在记录序列中顺序有序）：

公式好像给错了，比较的次数就是n-1次。

②最坏的情况（关键字在记录中逆序有序）：

③若待排序的序列是随机的，即待排序序列中的记录 可能出现的各种排列的概率相同，则：

平均情况下：

“比较”的次数： 最好和最坏的平均值，约为(n^2)/4 ；

“移动”的次数： 最好和最坏的平均值,  约为(n^2)/4。

时间：O(n^2)

空间：辅助空间1个，O(1)。

3）C++完整代码：

//插入排序
#include 
using namespace std;
void InsertSort(int a[],int n)
{
    int i, j, k;

    for (i =1;i=0;j--){
            if (a[j]j;k--)
                a[k+1] = a[k];
            //将a[i]放到正确位置上
            a[k+1] = temp;
        }
    }
}

int main()
{
	int Array[]={49,38,65,97,76,13,27,49,10};
	int Size= sizeof(Array) / sizeof(int);
    cout<

（5）折半插入分类

1）基本思想

因为R[1..i-1]是一个按关键字有序的有序序列，则可以 利用 折半查找 实现“在R[1..i-1]中查找R[i]的插入位置”， 如此实现的插入排序为折半插入排序。 

第i趟描述为：

①在[R1..Ri-1]中采用折半查找,查找位置j，满足： Rj.key<=Ri.key

②找到位置后，移动元素；

③插入到 正确位置，Rj:= R0
2）效率分析：

与直接插入比较，该方法的“比较“次数减少了 许多, O(nlog2n)。 “移动”次数没有减少，O(n2)。

时间：O(n^2)

空间：辅助空间1个，O(1)。

2-路分类和SHELL分类我就不说了，我们这没讲，应用好像也不是很多。

 

三、交换分类方法

（1）定义：假设待分类记录集合为 R1,R2,...Rn，简记为R[1..n]。 交换分类方法由多趟组成，假设要进行某一趟，它是 借助对无序序列中的记录进行“交换”的操作，将无序 序列中某关键字（最大、最小或其它）的记录“交换” 到该记录应该在的位置上。 

（2）根据比较交换的方法不同，交换分类也分为很多方法：

1）标准交换分类（冒泡分类）

2）成对交换分类（奇偶交换分类）

3）穿梭分类

4）快速分类

（3）冒泡分类方法

1）基本思想：整个分类过程由多趟组成：

①第1趟： r[n]与r[n-1]比较，逆序则交换；

r[n-1]与r[n-2]比较，逆序则交换；

... r[2]与r[1]比较，逆序则交换；

于是：r[1] 是无序序列中最小的！ 

②第i趟：r[n]与r[n-1]比较，逆序则交换；

r[n-1]与r[n-2]比较，逆序则交换；

... r[i+1]与r[i]比较，逆序则交换；

于是：r[i] 是无序序列中最小的！

重复，直到某趟中没有逆序发生为止。

2）效率分析

①最好：若序列已经正序排列时，仅需进行一趟，n-1次比较没有交换；

②最坏：如果序列是逆序排列的，需要进行n-1趟：

3）C++代码：

#include 

using namespace std;

void BubbleSort(int Array[],int Size){
    int i,j;
    for(i=0;iArray[j+1]){
                int temp = Array[j];
                Array[j] = Array[j+1];
                Array[j+1] = temp;
            }
        }
    }
    for(int i=0;i

（4）穿梭（交换）分类方法

1）基本思想：整个分类过程只有一趟，但是这一趟时停时进，具体地：

①一次比较：r[1]与r[2]比较，正序则一次比较继续，

                      r[2]与r[3]比较，......， 若r[i]与r[i+1]比较出现逆序，则交换， 一次比较停止，转而进行二次比较； 

②二次比较：一次比较逆序交换后，r[i]与r[i-1]比较，逆序则交换，然后r[i-1]与r[i-1]比较, 直到正序，然后继续一次比较（从一次比较停止的位置），即发现小元素，尽可能向上走。

（5）快速分类方法（快速排序）

1）基本思想：在待分类序列中指定一个元素，它称为 “轴”元素，然后经过一些操作把轴元素安置好，即把它安置在排好序后应该在的位置，亦即，它不小于前面的元素，不大于后面的元素 。安置好的轴元素将分类序列分为左右两部分，对这两部分利用同样的策略进行分类（递归）。

2）具体步骤：

假设待分类序列为 {r[s],r[s+1],...,r[t]}，整个分类有多趟组成：一趟过程如下： 

①首先任意选取一个记录作为轴元素，一般选取序列的第1个元素；

② 重新排列其余元素，凡其关键字小于枢轴的记录均移动至该记录之前，反之，凡关键字大于枢轴的记录均移动至该记录之后。从而得到轴元素的所在位置i；

③安置轴元素，轴元素将原序列分为两个子序列： {r[s],r[s+1],...,r[i-1]}  {r[i+1],r[i+2],...,r[t]} ；

④分别对分割所得两个子序列进行快速排序，依次类推，直至每个子序列中只含一个记录为止。

3）确定轴元素的位置：设轴元素为序列的第一个元素

附设两个指针i、j，初始值分别为s和t，轴元素rp=r[s]

①j从当前位置向前搜索找到第1个比轴元素小的记录，把该元素交换到前面；(与rp交换) 

②i从当前位置向后搜索找到第1个比轴元素大的记录，把该元素交换到后面；(与rp交换)

可以发现，轴元素左、右跳跃，最后落在最终位置上。而实际上前面的交换都是多余的，只要找到最终的位置 把rp放置到最后的位置即可。

（4）效率分析：

该算法是一个递归算法，按照递归算法的时间复杂性分析方法，假设一次划分所得枢轴位置i=k，则对n个记录进行快排所需时 间可由递归方程表示： 

若待排序列中记录的关键字是随机分布的，则k取1至n中任意 一值的可能性相同，由此可得快速排序所需时间的平均值为：

1）最坏情况：： 当待排序序列基本有序时，快速分类蜕化为冒泡分类，时间复杂性为O(n2)。

2）最好情况：每次都将轴元素安置在序列的中间，序列在最快的 时间内蜕化为长度是１的序列。O(nlogn)。

 

四、选择分类方法

1.选择分类方法的基本思想：假设待分类记录集合为 R1,R2,...Rn，简记为R[1..n]。 选择分类方法由多趟组成，假设要进行某一趟，它是 在当前无序序列中选择出“最小”或“最大”的记录 ，然后将它加入到有序序列中。

每一趟在n-i+1个记录中选取关键字最小的记录作为有序序列中的第i个记录。

2.根据选择最小或最大元素的方法不同，选择分类也分为很多方法：

简单选择分类

树选择分类（锦标赛分类）

堆分类

3.简单选择分类方法

（1）基本思想：每次从无序序列中采用简单选择方法选择最小的元素。

（2）具体步骤为：

整个分类共有n-1趟，

1）第一趟，r[1]与r[2], r[3], ..., r[n]比较，得到最小元素 放置在r[1]中； 

2）第二趟，r[2]与r[3], r[4], ..., r[n]比较，得到最小元素 放置到r[2]中；

3）r[n-1]与r[n]比较，得到最小元素，放置到 r[n-1]中；

3）效率分析：

对n个记录进行简单选择排序，所需进行的关键字间的比较次数总计为：n*(n-1)/2次。

移动次数，最小为0，最大为3*(n-1)。

4.锦标赛（树型）选择分类方法

（1）基本思想：

用更快的方法选择出最小元素，方法是：

首先，对n个记录的关键字进行两两比较，然后在其中[n/2]个较小者之间再进行两两比较，如此重复，直至选出最小关键记录为止。

然后，根据关系的可传递性，将叶子结点中的最小关键字改为“最大值”，然后从该叶子结点开始， 和其左（或右）兄弟的关键字比较，修改从叶子结点到根的路径上各结点的关键字，则根结点关键字 即为次小的关键字。

同理，可以依此从小到大找出所有关键字。 

上面这段描述不是很好理解，下面放一张图片：

（2）效率分析：

1）时间： 第1趟，求最小值的比较次数为：n/2+n/4+n/8+...+2+1；

第2—n-1趟，比较次数为logn；

因此，时间复杂性为：O(nlogn);

2）空间：有较多的辅助空间，n-1个（2n-1-n）

5.堆分类方法

（1）堆的特点：若序列是最小堆（小顶堆），则K1必是序列中的最小值； 若序列是最大堆（大顶堆），则K1必是序列中的最大值；

（2）堆分类的基本思想：

设待分类序列为r[1],r[2],r[3],...,r[n]，根据堆的性质， 把该序列调整为堆（最大堆或最小堆），则堆顶元 素为最大（最小）值，把该元素加入到有序序列中； 对剩余的无序序列，再调整为堆，得到次大元素， 加入到有序序列中，........，依次下去，直到无序序 列只有一个元素为止。具体地，整个分类有n-1趟： 

第一趟，将原始待分类序列调整为堆，求出最小值，加入到有序序列中； 

第i趟，把剩余的元素序列再调整为堆，取堆顶元素，加入到有序序列中。

（3）效率分析：

1）对深度为k的堆，“筛选”所需进行的关键字比较的次数 至多为2(k-1); 

2）对n个关键字，建成深度h=(log2n)+1的堆，所需进行的关键字比较的次数至多为4n次；

3）调整“堆顶”n-1次，总共进行的关键字比较的次数不超过：

因此，堆排序的时间复杂度为O(nlogn)。

 

五、归并分类方法的基本思想

将两个或两个以上的有序子序列“归并”为一个有序序列。

1.  2-路归并分类方法

（1）基本思想：待分类序列为r[1],r[2],...,r[n]。开始，每个元素看作一个有序 序列，分类分为log2n趟： 

第一趟：r[1]与r[2]，r[3]与r[4],...,两两归并，得到n/2个有序序列；

 第二趟：对上一趟的n/2有序序列，再两两归并，得到n/4个有序序列；

。。。。。。

最后一趟，得到最终的有序序列。

 （2）举个例子：

（3）效率分析：

1）归并两个长度为m,n的有序序列，最大比较次数为m+n;

2）归并长度为n的序列，共需要进行log2n;
时间复杂性：O(nlog2n) ；
空间复杂性：O(n)，即r2的大小；

 

最后，说一下各种分类方法的综合比较

1.时间性能

（1）按平均的时间性能来分，有三类排序方法：

1）时间复杂度为O(nlogn)的方法有：快速排序、堆排序和 归并排序，其中以快速排序为最好；

2）时间复杂度为O(n2)的有：直接插入排序、起泡排序和 简单选择排序，其中以直接插入为最好，特别是对那些 对关键字近似有序的记录序列尤为如此；

3）时间复杂度为O(n)的排序方法只有，基数排序。 

（2）按最好的时间性能来分，有三类排序方法：

当待排记录序列按关键字顺序有序时，直接插入排序和起泡排序能达到O(n)的时间复杂度;而对于快速排序而言， 这是最不好的情况，此时的时间性能蜕化为O(n2)，因此 是应该尽量避免的情况。

（3）简单选择排序、堆排序和归并排序的时间性能不随记录 序列中关键字的分布而改变。

2.空间性能

指的是排序过程中所需的辅助空间大小。

（1）所有的简单排序方法(包括：直接插入、起泡和简单选择) 和堆排序的空间复杂度为O(1)；

（2）快速排序为O(logn)，为栈所需的辅助空间；

（3）归并排序所需辅助空间最多，其空间复杂度为O(n )；

（4）链式基数排序需附设队列首尾指针，则空间复杂度为O(rd)。

3.排序方法的稳定性能

稳定的排序方法指的是，对于两个关键字相等的记录，它们在序列中的相对位置，在排序之前和经过排序之后，没有改变。
（1）当对多关键字的记录序列进行LSD方法排序时，必须采用 稳定的排序方法。 

（2）对于不稳定的排序方法，只要能举出一个实例说明即可。

（3）快速排序和堆排序是不稳定的排序方法。