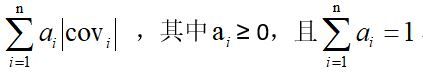python-OpenCV之边缘检测

简述

边缘指像素值急剧变化的位置。对于识别物体而言，边缘起着非常重要的作用。边缘检测的目的是在不损害图像内容的情况下制作一个线图。其方式依然是以卷积为核心操作。

知识点

1.有时需要将原图片分别与若干个卷积核进行卷积，这时需要将各个卷积结果进行最终整合，整合的方式主要有以下四种方式

• 取对应位置绝对值的和
• 取对应位置平方和的开方
• 取对应位置绝对值的最大值
• 插值法：

2.因为像素值的范围为0~255，所以图片数组最后的数据类型应该为unit8

Roberts边缘检测

Roberts算子是边缘检测中最简单的算子，利用差分定义生成。

检测流程

1.分别用45°方向差分的卷积算子和135°方向差分的卷积算子对图像进行卷积

2.将上述两个卷积结果进行整合

3.对最后结果进行整理（规范像素值）

说明：

1.scipy库中的convolve2d函数可进行二维数组的卷积，其语法为  scipy.signal.convolve2d(in1, in2, mode='full', boundary='fill', fillvalue=0)

代码示例

import cv2 as cv
import numpy as np
from scipy import signal


# 定义roberts函数
def roberts(I, _boundary='full', _fillvalue=0):
    # 获得原图片的尺寸
    H1, W1 = I.shape[0:2]
    # 定义算子尺寸
    H2, W2 = 2, 2

    # 进行45°方向卷积
    # 定义45°方向卷积核
    R1 = np.array([[1, 0], [0, -1]], np.float32)
    # 锚点位置
    kr1, kc1 = 0, 0
    # 进行卷积
    IconR1 = signal.convolve2d(I, R1, mode='full', boundary=_boundary, fillvalue=_fillvalue)
    # 截取得到same卷积
    IconR1 = IconR1[H2 - kr1 - 1:H1 + H2 - kr1 - 1, W2 - kc1 - 1:W1 + W2 - kc1 - 1]

    # 进行135°方向卷积
    R2 = np.array([[0, 1], [-1, 0]], np.float32)
    kr2, kc2 = 0, 1
    IconR2 = signal.convolve2d(I, R2, mode='full', boundary=_boundary, fillvalue=_fillvalue)
    IconR2 = IconR2[H2 - kr2 - 1:H1 + H2 - kr2 - 1, W2 - kc2 - 1:W1 + W2 - kc2 - 1]

    return (IconR1, IconR2)


if __name__ == "__main__":
    # 读取图片
    image = cv.imread('test2.jpg', flags=0)
    cv.imshow('original_Image', image)

    # 进行roberts边缘检测
    IconR1, IconR2 = roberts(image, 'symm')

    # 取图片数组各值的绝对值
    IconR1 = np.abs(IconR1)
    # RGB图像的深度应为8位
    edge_45 = IconR1.astype(np.uint8)
    cv.namedWindow('edge_45', cv.WINDOW_NORMAL)
    cv.imshow('edge_45', edge_45)

    IconR2 = np.abs(IconR2)
    edge_135 = IconR2.astype(np.uint8)
    cv.namedWindow('edge_135', cv.WINDOW_NORMAL)
    cv.imshow('edge_135', edge_135)

    # 将45°方向卷积结果和135°方向卷积结果平方后求和在开方求得
    edge = np.sqrt(np.power(IconR1, 2.0) + np.power(IconR2, 2.0))
    edge = np.round(edge)
    # 因为是两个图片的‘叠加‘，所以存在大于255的风险，将大于255的像素值都取255
    edge[edge > 255] = 255
    edge = edge.astype(np.uint8)
    cv.namedWindow('edge', cv.WINDOW_NORMAL)
    cv.imshow('edge', edge)

    cv.waitKey()
    cv.destroyAllWindows()

原图

45°方向卷积核卷积结果

135°方向卷积核卷积结果

整合后效果

prewitt边缘检测

prewitt算子可以看出是均值平滑算子和Roberts算子卷积后的结果，因此他兼具平滑和检测功能。

检测流程

1.对图像的竖直/水平方向进行平滑

2.对图像的水平/竖直方向进行差分

3.将水平和竖直方向上的差分结果进行整合

4.对最后结果进行整理（规范像素值）

代码示例

import cv2 as cv
import numpy as np
from scipy import signal


def prewitt(I, _boundary='symm'):
    # 先对竖直方向进行平滑
    ones_y = np.array([[1], [1], [1]], np.float32)
    i_conv_pre_x = signal.convolve2d(I, ones_y, mode='same', boundary=_boundary)
    # 再对水平方向进行差分
    diff_x = np.array([[1, 0, -1]], np.float32)
    i_conv_pre_x = signal.convolve2d(i_conv_pre_x, diff_x, mode='same', boundary=_boundary)

    # 对水平方向进行平滑
    ones_x = np.array([[1, 1, 1]], np.float32)
    i_conv_pre_y = signal.convolve2d(I, ones_x, mode='same', boundary=_boundary)
    # 对竖直方向进行差分
    diff_y = np.array([[1], [0], [-1]], np.float32)
    i_conv_pre_y = signal.convolve2d(i_conv_pre_y, diff_y, mode='same', boundary=_boundary)

    return (i_conv_pre_x, i_conv_pre_y)


if __name__ == "__main__":
    # 读取图片，注意，要读入灰度图
    image = cv.imread('test.jpg', flags=0)
    # 显示原图片
    cv.namedWindow('dfs', cv.WINDOW_NORMAL)
    cv.imshow('dfs', image)
    
    # 调用已写好的函数进行卷积
    i_conv_pre_x, i_conv_pre_y = prewitt(image)

    # 对图像数组的数值取绝对值
    abs_i_conv_pre_x = np.abs(i_conv_pre_x)
    abs_i_conv_pre_y = np.abs(i_conv_pre_y)

    # 重新复制一份结果，后面合成最终结果时会用到
    edge_x = abs_i_conv_pre_x.copy()
    edge_y = abs_i_conv_pre_y.copy()

    # 将超出255的赋值为255
    edge_x[edge_x > 255] = 255
    edge_y[edge_y > 255] = 255

    # 因为色素的数值范围为0~255，所以应该设置为unit8数据类型
    edge_y = edge_y.astype(np.uint8)
    edge_x = edge_x.astype(np.uint8)

    cv.namedWindow('edge_x', cv.WINDOW_NORMAL)
    cv.imshow("edge_x", edge_x)

    cv.namedWindow('edge_y', cv.WINDOW_NORMAL)
    cv.imshow('edge_y', edge_y)

    # 将两个结果合并
    # 有多种合并方法，这里用的时插值法
    edge = abs_i_conv_pre_x * 0.5 + abs_i_conv_pre_y * 0.5
    edge[edge > 255] = 255
    edge = edge.astype(np.uint8)
    
    cv.namedWindow('edge', cv.WINDOW_NORMAL)
    cv.imshow('edge', edge)
    cv.waitKey()
    cv.destroyAllWindows()

原图​​​​​

x方向上进行差值

y​​​​​方向上进行差值

整合后效果

Sobel边缘检测

Sobel算子跟Prewitt算子类似，也自带平滑效果，只不过它的平滑不是非归一均值平滑而是非归一高斯平滑。

检测流程

1.对图像的竖直/水平方向进行平滑

2.对图像的水平/竖直方向进行差分

3.将水平和竖直方向上的差分结果进行整合

4.对最后结果进行整理（规范像素值）

代码示例

import math
import cv2 as cv
import numpy as np
from scipy import signal


# 理论上sobel算法采用高斯平滑的算子，应该比prewitt对“明显”的边缘更加敏感
# 返回n阶非归一化的高斯平滑算子
def pascalSmooth(n):
    # 这里的数组必须为二维，因为后面的convoluted函数要求的输入必须为二维数组
    pascalSmooth = np.zeros([1, n], np.float32)
    for i in range(n):
        # math.factorial(x)函数返回x的阶乘
        pascalSmooth[0][i] = math.factorial(n - 1) / (math.factorial(i) * math.factorial(n - 1 - i))
    return pascalSmooth


# 由高斯平滑算子得到差分算子，并返回差分算子
def pascalDiff(n):
    pascalDiff = np.zeros([1, n], np.float32)
    pascalSmooth_previous = pascalSmooth(n - 1)
    for i in range(n):
        if i == 0:
            pascalDiff[0][i] = pascalSmooth_previous[0][i]
        elif i == n - 1:
            pascalDiff[0][i] = -pascalSmooth_previous[0][i - 1]
        else:
            pascalDiff[0][i] = pascalSmooth_previous[0][i] - pascalSmooth_previous[0][i - 1]
    return pascalDiff


# 得到sobel算子
def getSobelKernel(n):
    pascalSmoothKernel = pascalSmooth(n)
    pascalDiffKernel = pascalDiff(n)
    # np.transpose的功能是将矩阵转置
    sobelKernal_x = signal.convolve2d(pascalSmoothKernel.transpose(), pascalDiffKernel, mode='full')
    sobelKernal_y = signal.convolve2d(pascalSmoothKernel, pascalDiffKernel.transpose(), mode='full')

    return (sobelKernal_x, sobelKernal_y)


# sobel边缘检测核心函数
def sobel(image, n):
    # rows, cols = image.shape
    pascalSmoothKernel = pascalSmooth(n)
    pascalDiffKernel = pascalDiff(n)

    image_sobel_x = signal.convolve2d(image, pascalSmoothKernel.transpose(), mode='same')
    image_sobel_x = signal.convolve2d(image_sobel_x, pascalDiffKernel, mode='same')

    image_sobel_y = signal.convolve2d(image, pascalSmoothKernel, mode='same')
    image_sobel_y = signal.convolve2d(image_sobel_y, pascalDiffKernel.transpose(), mode='same')

    return (image_sobel_x, image_sobel_y)


if __name__ == "__main__":
    image = cv.imread('test4.jpg', flags=0)
    cv.namedWindow('original', cv.WINDOW_NORMAL)
    cv.imshow('original', image)
    # 进行sobel卷积
    sobel_x, sobel_y = sobel(image, 7)
    # 归一化处理
    image_sobel_x = sobel_x / np.max(sobel_x)
    image_sobel_y = sobel_y / np.max(sobel_y)
    image_sobel_x = np.power(image_sobel_x, 1)
    image_sobel_y = np.power(image_sobel_y, 1)
    # 数值化
    image_sobel_x = image_sobel_x * 255
    image_sobel_y = image_sobel_y * 255
    image_sobel_x = image_sobel_x.astype(np.uint8)
    image_sobel_y = image_sobel_y.astype(np.uint8)
    # 显示不同方向的sobel卷积结果
    cv.namedWindow('sobel_x', cv.WINDOW_NORMAL)
    cv.namedWindow('sobel_y', cv.WINDOW_NORMAL)
    cv.imshow('sobel_x', image_sobel_x)
    cv.imshow('sobel_y', image_sobel_y)

    # 对两个方向的处理结果进行整合
    edge = np.sqrt(np.power(sobel_x, 2.0), np.power(sobel_y, 2.0))
    edge = edge / np.max(edge)
    edge *= 255
    edge = edge.astype(np.uint8)
    cv.namedWindow('sobel', cv.WINDOW_NORMAL)
    cv.imshow('sobel', edge)
    cv.waitKey()
    cv.destroyAllWindows()

原图

x方向差分的sobel算子处理结果

y方向差分的sobel算子处理结果

两个方向整合后的最终结果

OpenCV API

函数语法：Sobel( src, ddepth, dx, dy, ksize, scale, borderType )

参数	解释
src	输入矩阵
ddepth	输出矩阵的数据类型
dx	当dx ≠ 0时，src与差分方向为水平方向上的Sobel核卷积
dy	当dx = 0，dy ≠ 0时，src与差分方向为垂直方向上的Sobel核卷积
ksize	Sobel核的尺寸，值为1，3，5，7
Scale（可选）	比例系数
Delta（可选）	平移系数
borderType（可选）	边界扩充类型

Canny边缘检测

基于卷积运算的边缘检测算法，如Sobel和Prewitt等有以下两个缺点：

1.没有充分利用边缘的梯度

2.最后输出的边缘二值图只是简单地利用阈值进行处理，容易损失信息。

Canny算法基于这两点做了改进，提出了：

1.基于边缘梯度方向的非极大值抑制

2.双阈值的滞后阈值处理

检测流程

1.高斯平滑去噪

2.计算梯度方向

3.非极大值抑制

4.双阈值的滞后阈值处理

示例代码

import math

import Sobel
import cv2 as cv
import numpy as np


# 非极大值抑制函数，返回“极大值”矩阵
def non_maximum_suppression_default(dx, dy):
    # dx和dy为经过水平差分算子和垂直差分算子卷积后的数值矩阵（sobel或者prewitt）
    edgeMag = np.sqrt(np.power(dx, 2.0), np.power(dy, 2.0))
    rows, cols = edgeMag.shape

    # 梯度矩阵（边缘强度）
    # gradientDirection = np.zeros(edgeMag.shape)
    # 非极大值抑制后的矩阵
    edgeMag_nonMaxSup = np.zeros(edgeMag.shape)

    for r in range(1, rows - 1):
        for c in range(1, cols - 1):
            angle = math.atan2(dy[r][c], dx[r][c]) / math.pi * 180
            # gradientDirection[r][c] = angle
            # 判断差值方向
            # 左右方向
            if (abs(angle) < 22.5 or abs(angle) > 157.5):
                if (edgeMag[r][c] > edgeMag[r][c - 1] and edgeMag[r][c] > edgeMag[r][c + 1]):
                    edgeMag_nonMaxSup[r][c] = edgeMag[r][c]
            # 左上/右下方向
            if (angle >= 22.5 and angle < 67.5 or (-angle > 112.5 and -angle <= 157.5)):
                if (edgeMag[r][c] > edgeMag[r - 1][c - 1] and edgeMag[r][c] > edgeMag[r + 1][c + 1]):
                    edgeMag_nonMaxSup[r][c] = edgeMag[r][c]
            # 上下方向
            if (abs(angle) >= 67.5 and abs(angle) <= 112.5):
                if (edgeMag[r][c] > edgeMag[r - 1][c] and edgeMag[r][c] > edgeMag[r + 1][c]):
                    edgeMag_nonMaxSup[r][c] = edgeMag[r][c]
            # 右上/左下方向
            if ((angle > 112.5 and angle <= 157.5) or (-angle >= 22.5 and -angle < 67.5)):
                if (edgeMag[r][c] > edgeMag[r - 1][c + 1] and edgeMag[r][c] > edgeMag[r + 1][c - 1]):
                    edgeMag_nonMaxSup[r][c] = edgeMag[r][c]

    return edgeMag_nonMaxSup


# 判断一个点的坐标是否在图像内
def checkInRange(r, c, rows, cols):
    if r >= 0 and r < rows and c >= 0 and c < cols:
        return True
    else:
        return False


# 在已有高于阈值点的情况下确定边缘点
def trace(edgeMag_nonMaxSup, edge, lowerThresh, r, c, rows, cols):
    if edge[r][c] == 0:
        # 将符合“边缘”要求的像素值都设置为255
        edge[r][c] = 255
        for i in range(-1, 2):
            for j in range(-1, 2):
                # 大于低阈值便视为边缘
                if checkInRange(r + i, c + j, rows, cols) and edgeMag_nonMaxSup[r + i][c + j] >= lowerThresh:
                    # 这里用递归遍历周围的像素点
                    trace(edgeMag_nonMaxSup, edge, lowerThresh, r + i, c + j, rows, cols)


# 滞后阈值处理
def hyteresisThreshold(edge_nonMaxSup, lowerThresh, upperThresh):
    rows, cols = edge_nonMaxSup.shape
    # 新创建一个用于存储边缘的数组
    edge = np.zeros(edge_nonMaxSup.shape, np.uint8)
    for r in range(1, rows - 1):
        for c in range(1, cols - 1):
            # 如果大于高阈值，就确定与其相连的边缘点
            if edge_nonMaxSup[r][c] >= upperThresh:
                trace(edge_nonMaxSup, edge, lowerThresh, r, c, rows, cols)
            # 如果低于低阈值，就直接舍弃
            if edge_nonMaxSup[r][c] < lowerThresh:
                edge[r][c] = 0
    return edge


if __name__ == "__main__":
    image = cv.imread('test2.jpg', flags=0)
    cv.imshow('original', image)

    image_sobel_x, image_sobel_y = Sobel.sobel(image, 3)
    edge = np.sqrt(np.power(image_sobel_x, 2.0), np.power(image_sobel_y, 2.0))
    edge[edge > 255] = 255
    edge = edge.astype(np.uint8)
    cv.namedWindow('sobel', cv.WINDOW_NORMAL)
    cv.imshow('sobel', edge)

    # 抑制非极大值
    edgeMag_nonMaxSup = non_maximum_suppression_default(image_sobel_x, image_sobel_y)

    edgeMag_nonMaxSup[edgeMag_nonMaxSup > 255] = 255
    edgeMag_nonMaxSup = edgeMag_nonMaxSup.astype(np.uint8)
    cv.namedWindow('edgeMag_nonMaxSup', cv.WINDOW_NORMAL)
    cv.imshow('edgeMag_nonMaxSup', edgeMag_nonMaxSup)

    lowerThresh = 40
    upperThresh = 150
    edge = hyteresisThreshold(edgeMag_nonMaxSup, lowerThresh, upperThresh)
    cv.namedWindow('canny', cv.WINDOW_NORMAL)
    cv.imshow('canny', edge)

    cv.waitKey()
    cv.destroyAllWindows()

原图

sobel卷积后的图片​​​​​

抑制非极大值后的图片

canny边缘检测最终效果

OpenCV API

函数语法：Canny(image, edges, threshold1, threshole2, apertureSize, L2gradient )

参数	解释
image	输入图像
threshold1	低阈值
threshold2	高阈值
Edges(可选)	输出边缘强度图像
apertureSize(可选)	Sobel核的窗口大小，默认3×3
L2gradient(可选)	计算总的边缘强度时使用的方式，值为true时代表使用的是平方和开方的方式，值为false代表使用的是绝对值和的方式。

Laplacian边缘检测

import cv2 as cv
import numpy as np
from scipy import signal


# 核心步骤，拉普拉斯卷积核与图像矩阵进行卷积
def laplacian(image, _boundary='full', _fillvalue=0):
    laplacianKernel = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]], np.float32)
    i_conv_lap = signal.convolve2d(image, laplacianKernel, mode='same', boundary=_boundary, fillvalue=_fillvalue)

    return i_conv_lap


if __name__ == "__main__":
    image = cv.imread('test5.jpg', flags=0)
    cv.imshow('original', image)
    image = np.array(image)
    # 对图像进行高斯平滑
    image = cv.GaussianBlur(image, (3, 3), 0)
    # 调用拉普拉斯核卷积函数
    threshEdge = laplacian(image, 'symm')

    # 进行阈值处理
    threshEdge[threshEdge > 0] = 255
    threshEdge[threshEdge < 0] = 0
    threshEdge = threshEdge.astype(np.uint8)
    cv.imshow('threshEdge', threshEdge)

    cv.waitKey()
    cv.destroyAllWindows()

OpenCV API

函数语法：placian(src, dst, ddepth, ksize, scale, delta, borderType )

参数	解释
src	输入矩阵
dst	输出矩阵
ddepth	输出矩阵的数据类型（位深）
Ksize(可选)	Laplacian核的类型
Scale(可选)	比例系数
delta(可选)	平移系数
borderType(可选)	边界扩充类型