Python实现《都挺好》社交网络分析

1《都挺好》简介

该小说讲述了职场金领苏明玉从小不受家人待见，生长在家庭的边缘，在孤独扭曲的环境中长大成人的故事。结局是这样的，苏明哲回到了美国，苏明成和朱丽离婚后不知所踪，苏明玉和石天冬在一起了，三个子女看清了苏大强的为人，没有人再管着他，最终苏大强得了老年痴呆症，苏明玉于心不忍，因此把他接回家照顾。

上图是去除停用词、去除人名、只保留形容词和名词的小说词云图；由图中也可以看出基本都是和家庭相关的词语。

# 小说词云
def getWordCloud():
    rlist=[]
    for s in content:
        for w in pseg.cut(str(s)):
            if(w.word not in stopdict and w.flag=='a' or w.flag=='n'):
                rlist.append(w.word)
    rlist = " ".join(rlist)
    w = WordCloud(font_path="C:/Users/Windows/fonts/simkai.ttf",width=600,height=400,background_color="black",max_words=50)
    w.generate(rlist)
    path=r'C:\Users\Administrator\Desktop\pic.png'
    w.to_file(path)

2人物共同出现频数

2.1制作主要人物字典

需要把《都挺好》小说txt版下载下来，刚开始我是通过jieba分词把所有nr(人名)的词语保存下来，作为人物集合，但是①某个人物多个称呼 ②nr类型会出现许多不合适的词

words=pseg.cut(single)
        for w in words:
            if(w.flag=='nr')

参考电视猫中的人物关系图，单独制作了主要人物词典

#主要人物 姓名词典
pdict={'明玉':['明玉','苏明玉','苏总'],'朱丽':['朱丽','丽丽'],'明哲':['明哲','苏明哲','大哥'],
       '明成':['明成','苏明成','大哥'],'苏大强':['苏大强','老爹','爸'],'吴非':['吴非'],'苏家':['苏家'],
       '宝宝':['宝宝'],'老蒙':['老蒙','蒙总'],'小蒙':['小蒙'],'天冬':['天冬','石天冬','石大哥'],
       '柳青':['柳青'],'蔡根花':['蔡根花'],'钟点工':['钟点工'],'温玮光':['温玮光','温总'],'苏母':['苏母']}

#判断na是哪个人物
def getPerson(na):
    for key,value in pdict.items():
        if(na in value):
            return str(key)
    return '无'

2.2计算人物相互出现的频数

（1）首先初始化一个16×16的人物频数0矩阵。
（2）在小说的每一段中，当这一段中出现了词典中的人物时，就把出现的人物两两对应的频数+1。
（3）遍历频数矩阵的右上半边（或左下半边）获得人物两两之间的频数。

# 计算人物相互出现的频数 保存成顶点-权重
def getPeopleNetwork():
    plist=list(pdict.keys())
    N=len(plist)
    pcount=np.zeros([N,N])
    #初始化 人物频数 二维矩阵
    pcount=pd.DataFrame(data=pcount,columns=plist,index=plist)
   
    #遍历每一段，出现的人物 频数+1
    for sentence in content:
        s_plist=[]#出现的人物集合
        words=jieba.cut(sentence)
        for w in words:
            if(getPerson(w)!='无' and getPerson(w) not in s_plist):
                s_plist.append(getPerson(w))
        #根据出现的人物集合 进行频数+1
        for p1 in s_plist:
            for p2 in s_plist:
                pcount.loc[p1][p2]+=1

    #保存频数二维矩阵
    pcount.to_excel('./data/人物频数矩阵.xlsx')
    print('w ok')

    #根据频数二维矩阵 计算 人物1-人物2-权重
    p_network=[]
    for i in np.arange(N):
        for j in np.arange(i+1,N):
            p_network.append([plist[i],plist[j],pcount.iloc[i,j]])

    #保存 边-权重
    p_network=pd.DataFrame(data=p_network,columns=['人物1','人物2','count'])
    p_network.to_excel('./data/权重.xlsx')
    print('w ok')

3绘制人物关系图

节点越大，代表该人物越重要。根据频数范围（400，200，100，30），将边划分成五个程度，红蓝黄紫橙，关系依次减弱。

一共有5条出现次数超过400的关系，其中3条关系是明哲、明成、明玉这三兄妹之间的关系，另外两条是明成、明玉和各自配偶的关系；而苏大强和三位子女的关系也较强，均超过200次，稍弱于三兄妹之间的关系。这表明《都挺好》小说主要围绕三兄妹和父亲进行剧情发展，这也符合我们的实际认知。

#画出第c1-c2章的社交网络图
def drawNetwork(c1,c2):
    data=pd.DataFrame(pd.read_excel('./data/权重-.xlsx',sheet_name=0)) 
    #data=data[data['人物1']!=data['人物2']]
    data=data[(data['chapter']>=c1)&(data['chapter']<=c2)]
    data=data.groupby([data['人物1'],data['人物2']])['count'].sum().reset_index()
    data=data[data['count']!=0]
    G=nx.Graph()
    for index,item in data.iterrows():
        G.add_weighted_edges_from([(item['人物1'],item['人物2'],item['count'])])
    pos = nx.spring_layout(G)
    nx.draw_networkx_labels(G,pos,font_size=11,font_family='simhei')#画标签
    nx.draw_networkx_nodes(G,pos,nodelist=list(nx.algorithms.pagerank(G).keys()),node_size=[x*3000 for x in list(nx.algorithms.pagerank(G).values())],node_color='lightgreen') 

    if(c1==1 and c2==40):
        #不同联系强度的边集合 
        degree1=[(x,y) for (x,y,z)in G.edges(data=True) if z['weight']<30]
        degree2= [(x, y) for (x, y, z) in G.edges(data=True) if 30<=z['weight'] < 100]
        degree3= [(x, y) for (x, y, z) in G.edges(data=True) if 100<=z['weight'] < 200]
        degree4= [(x, y) for (x, y, z) in G.edges(data=True) if 200<=z['weight'] < 400]
        degree5=[(x,y) for (x,y,z)in G.edges(data=True) if z['weight']>=400]

        #不同强度的边 宽度、颜色 不同
        nx.draw_networkx_edges(G, pos, edgelist=degree1, width=0.5, edge_color='orange')
        nx.draw_networkx_edges(G, pos, edgelist=degree2, width=1.5, edge_color='m')
        nx.draw_networkx_edges(G, pos, edgelist=degree3, width=3, edge_color='yellow')
        nx.draw_networkx_edges(G, pos, edgelist=degree4, width=4, edge_color='cornflowerblue')
        nx.draw_networkx_edges(G,pos,edgelist=degree5,width=6,edge_color='red')
    else:
        for e in G.edges(data=True):
            nx.draw_networkx_edges(G,pos,edgelist=[e],width=e[2]['weight']/10,edge_color='red')
 
    plt.axis('off')
    plt.title('第{}章到第{}章人物关系网络图'.format(c1,c2))
    plt.show()

4重要人物

调用PageRank算法，可以获得每个节点人物的pr值，我们以此值来衡量人物的重要程度。作为该小说的主角，明玉当仁不让位居第一；值得一提的是，三兄妹位于TOP3，三兄妹及其配偶、父亲苏大强七位人物位于TOP7。

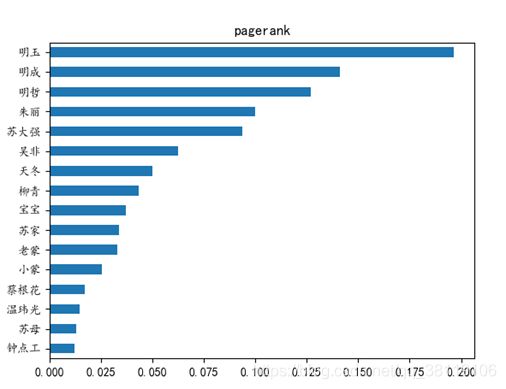
 page_ranks = pd.Series(nx.algorithms.pagerank(G)).sort_values()
 page_ranks.plot(kind="barh")
 plt.title('pagerank')
 plt.show()

5社区发现

结果将《都挺好》的剧情人物自动划分成两个社区：社区1是以明玉为代表的其配偶、生意伙伴；社区2是除了明玉以外的苏家人物集合。很明显，明玉由于从小在家里不受喜欢，长大后和整个苏家是联系较弱的（虽然内心还是有爱的）。可见算法生成的结果也是符合情理的。

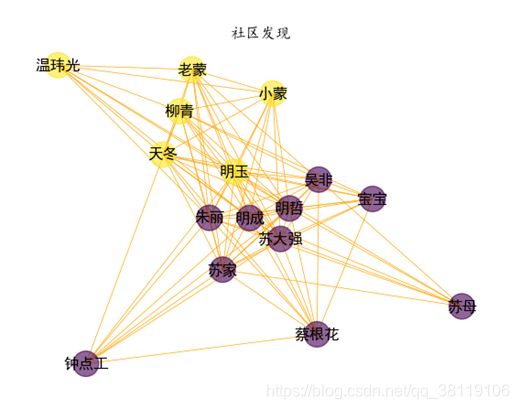
    #step2 画社区 都在一张图上
    part = community.best_partition(G)
    values = [part.get(node) for node in G.nodes()] #社区
    nx.draw_networkx_nodes(G,pos,alpha=0.6, node_color=values,node_size=400)
    nx.draw_networkx_edges(G,pos,edgelist=G.edges,width=0.5,edge_color='orange')
    nx.draw_networkx_labels(G,pos,font_size=12,font_family='simhei')
    plt.axis('off')
    plt.title('社区发现')
    plt.show()

6人物相关系数

相关系数（x,y）的值代表x和y的联系度，计算方式是x和y都出现的段落/x的段落。图中横着为y，纵着为x。比如人物x和人物y之间共同出现了100次，但是x出现了200次，y出现了1000次；显然y对于x来说更重要，因为y占据了x的50%，而x占据了y的10%。

（1）明玉整体来说对于其他人物来说都比较重要，她对于苏家、小蒙、天冬、柳青、温总的相关系数均超过0.6，除了钟点工和蔡根花，明玉对于其他人的相关系数也较强。
（2）明哲、明成、苏大强对于其他人物来说也较为重要。
（3）和苏大强联系最紧密的三位人物是：明哲-0.48、明成-0.46、明玉-0.33，这表明大儿子和二儿子对于苏大强的重要程度相近，都领先于三女儿对其的重要程度，小说中苏大强跟着二儿子住，一门心思想跟着大儿子去美国享福，所以两人的相关系数最高；这也侧面印证了明玉在苏家不那么受重视。
（4）和明玉联系最紧密的两位人物是明成-0.24和天冬-0.21，和明成联系紧密是因为两人矛盾冲突很大，小说中甚至有明成去殴打明玉的情节；和天冬联系紧密则是因为两人的情侣关系。
（5）有趣的是，对于蔡根花来说，苏大强是其最重要人物，相关系数高达0.65；作为苏大强的保姆，两人的黄昏恋可以说是让人啼笑皆非，在电视剧热播之后“蔡根花宝贝”、“图你年纪大、图你不洗澡”也成为流行一时的梗。

#人物相关系数
def getPeopleRelation():
    pcount=pd.DataFrame(pd.read_excel('./data/人物频数矩阵.xlsx',sheet_name=0,index_col=0))#第0列作索引
    N=pcount.shape[0]
    secondmax=0
    for i in np.arange(N):
        count=pcount.iloc[i][i]
        for j in np.arange(N):
            pcount.iloc[i,j]/=count
            #if(pcount.iloc[i,j]>secondmax and pcount.iloc[i,j]!=1):
            #    secondmax=pcount.iloc[i,j]
    print(pcount)
    ax = plt.axes() 
    im = ax.imshow(pcount,cmap=plt.cm.summer,interpolation='none',vmin=0,vmax=0.6,aspect='equal')#vmax如果是1，图会很稀疏
    plt.colorbar(im, shrink=0.5)
    plt.xticks(np.arange(N),list(pcount.index))
    plt.yticks(np.arange(N),list(pcount.index))
    plt.title('人物相关系数矩阵')
    plt.show()
    pcount.to_excel('./data/人物相关系数矩阵.xlsx')
    print('w ok')

7随时间变化的人物关系

下载得到的《都挺好》小说中有40章，每一章的标题都以对应的数字显示，因此可以计算人物频数时，再加一列数字来表明是第几章。我以每5章为一时间段，制作八个时间段的人物关系网络图。

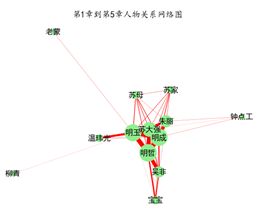
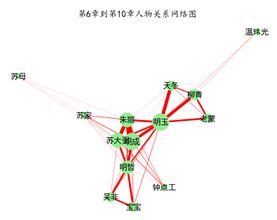
比如以上面两张图为例，分别是1-5章和6-10章的人物关系网络图。可以看出：前5章就主要是三兄妹家庭之间的联系；而6-10章明玉与天冬、柳青、老蒙的联系突然增强，可能这几章在讲明玉与苏家之间的关系的同时，也兼顾讲述了明玉工作上的情况，所以这些生意伙伴的联系突然增多。

为了显示某两个人物随时间变化的关系，我重新计算八个时间段内的某两个人物的出现次数和相关系数,挑选以下几个进行说明。

（1）明玉对于苏大强的相关系数
从第2时间段的0.2左右开始，明玉对于苏大强的相关系数一直随时间增加到第7时间段的0.45左右，最后一个时间段稍微减少至0.4左右；这表明明玉对于苏大强的重要性在前期较弱，但是随着时间发展，明玉越来越重要，直到最后重要性比第2时间段的重要性多了1倍；由于结局是明玉照顾得了老年痴呆的苏大强，所以明显在后面几个时间段，明玉对于苏大强的关联都较强。

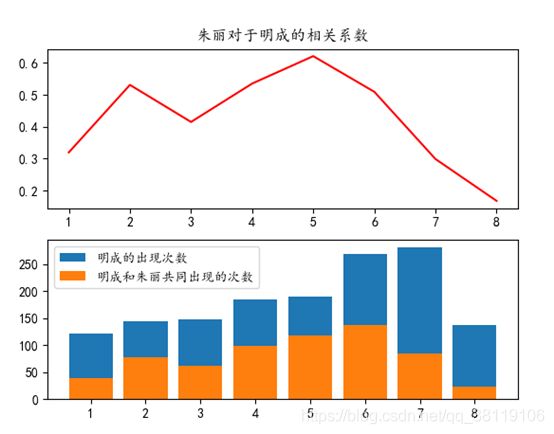
（2）朱丽对于明成的相关系数
从第5时间段的峰值0.6左右开始逐渐减弱，直至最后的0.1左右；这与小说中两人关系破裂最终离婚的剧情也是相符合的。

#获取人物关系随时间变化
def getTimePeople(p1,p2):
    data=pd.DataFrame(pd.read_excel('./data/权重-.xlsx',sheet_name=0)) 
    y=[] #相关系数
    y1=[]#p1出现次数
    y2=[]#p1 p2共同出现次数
    for c in np.arange(1,40,5): 
        mdata=data[(data['chapter']>=c)&(data['chapter']<=c+4)]
        mdata=mdata.groupby([mdata['人物1'],mdata['人物2']])['count'].sum().reset_index()
        mdata=mdata[(mdata['人物1']==p1)|(mdata['人物2']==p1)]
        for index,item in mdata[(mdata['人物1']==p1)&(mdata['人物2']==p1)].iterrows():
            count=item[2]
        y1.append(count)
        mdata=mdata[(mdata['人物1']==p2)|(mdata['人物2']==p2)]
        for index,item in mdata.iterrows():
            y2.append(item[2])
            y.append(item[2]/count if count>0 else 0)
 
    plt.figure()
    plt.subplot(2, 1, 1)
    plt.title('{p2}对于{p1}的相关系数'.format(p2=p2,p1=p1))
    plt.plot(np.arange(1,9),y,color='red')
    plt.subplot(2, 1, 2)
    plt.bar(np.arange(1,9),y1)
    plt.bar(np.arange(1,9),y2)
    plt.legend(labels=['{p1}的出现次数'.format(p1=p1),'{p1}和{p2}共同出现的次数'.format(p1=p1,p2=p2)],loc='best')
    plt.show()

8最后

明玉从被苏家嫌弃的三女儿成长为职场女强人，映证着小说结尾的一句话，“自己过得好，才是一切”。在生活这张复杂网络下，每个人又何尝不是一个节点，不断努力丰富自己，也许才能更自主的选择周围的边和联系程度，也许有一天会发现自己所处的“小世界”一切都挺好。

问题：按照每段中出现了不同的人物，就两两进行频数+1的处理思路，但是这样同时有个问题，就是当一段中出现同一个人物不只一次时的情况如何处理，比如某一段出现了A3次，B2次，C1次：
①本作业中使用的是不重复统计，即AA BB CC AB AC BC BA BC CB的次数都+1；
②但是我个人感觉按次数计算也合理，即AA+3 BB+2 CC+1 AB+6 AC+3 BC+2 BA+6 CA+3 CB+2；刚开始我是这么计算的，进行社区发现之后的结果分成了三个社区：明玉及其生意伙伴；明成、朱丽、钟点工小家庭；明哲、苏大强以及苏家其他的人；当时认为这个社区发现结果很合理，三兄妹直接分成对应的三个社区，但是由于这样处理频数是虚高的，所以还是放弃了这种方法，直接用①方法进行处理。
所以针对人物共同出现频数，我也没有去细究如何处理。

参考文章：
https://blog.csdn.net/blmoistawinde/article/details/85344906
https://blog.csdn.net/csdnnews/article/details/84312510
https://blog.csdn.net/erin_hh/article/details/52938211