强化学习(Q-Learning,Sarsa)

Reinforcement Learning
监督学习–>非监督学习–>强化学习。
监督学习:拥有“标签”可监督算法不断调整模型,得到输入与输出的映射函数。
非监督学习:无“标签”,通过分析数据本身进行建模,发掘底层信息和隐藏结构。
在线学习:接受新数据,更新参数。
但是1.标签需要花大量的代价进行收集,在有些情况如子任务的组合数特别巨大寻找监督项是不切实际的。2.如何更好的理解数据,学习到具体的映射而不仅仅是数据的底层结构?
强化学习:
先行动起来,如果方向正确那么就继续前行,如果错了,子曰:过则勿惮改。吸取经验,好好改正,失败乃成功之母,从头再来就是。总之要行动,胡适先生说:怕什么真理无穷,进一寸有一寸的欢喜。
即想要理解信息,获得输入到输出的映射,就需要从自身的以往经验中去不断学习来获取知识,从而不需要大量已标记的确定标签,只需要一个评价行为好坏的奖惩机制进行反馈,强化学习通过这样的反馈自己进行“学习”。(当前行为“好”以后就多往这个方向发展,如果“坏”就尽量避免这样的行为,即不是直接得到了标签,而是自己在实际中总结得到的)
特点:
- 没有监督标签。只会对当前状态进行奖惩和打分,其本身并不知道什么样的动作才是最好的。
- 评价有延迟。往往需要过一段时间,已经走了很多步后才知道当时选择是好是坏。有时候需要牺牲一部分当前利益以最优化未来奖励。
- 时间顺序性。每次行为都不是独立的数据,每一步都会影响下一步。目标也是如何优化一系列的动作序列以得到更好的结果。即应用场景往往是连续决策问题。
- 与在线学习相比,强化学习方法可以是在线学习思想的一种实现,但是在线学习的数据流一定是增加的,而强化学习的数据可以做减少(先收集,更新时按丢掉差数据的方向)。而且在线学习对于获得的数据是用完就丢,强化学习是存起来一起作为既往的经验。

数学化表示
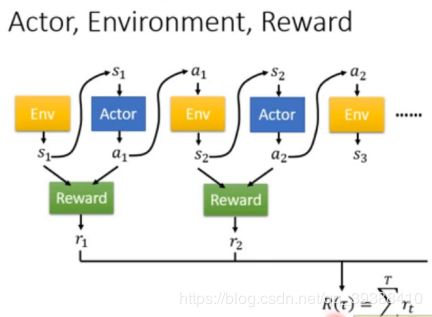
在时刻 t,由于当前对不可全知的环境,只能采取对环境的 observation 观察 O t O_t Ot,选择一个action 行为 A t A_t At,得到一个reward 奖励打分 R t + 1 R_{t+1} Rt+1,然后继续选择动作,循环往复。(当 A t A_t At的行为采用后,环境将会改变,而采取了 A t A_t At得到的奖励是在下一时刻出现的,即 R t + 1 R_{t+1} Rt+1)
所以 t 时刻所包含的整个历史过程会是: H t = O 1 , R 1 , A 1 , . . . , O t − 1 , R t − 1 , A t − 1 , O t , R t , A t H_t=O_1,R_1,A_1,...,O_{t-1},R_{t-1},A_{t-1},O_t,R_t,A_t Ht=O1,R1,A1,...,Ot−1,Rt−1,At−1,Ot,Rt,At
当前的 状态 S t S_t St 是所有已有信息序列的函数 S t = f ( H t ) S_t=f(H_t) St=f(Ht),用于决定未来的发展。
Policy π:表示所采用的行动。它是从状态 S到行为A的一个映射,可以是确定性的,也可以是不确定性的。即动作将会根据策略 π(a|s) 这一概率分布来进行选择。
Value:状态价值函数,每种动作可能带来的后续奖励,用于评估策略。因为只有一个当前奖励 reward 是远远不够的,当前奖励大并不代表其未来的最终奖励一定是最大的,所以需要使用 Value期望函数来评价未来。
v π ( s ) = E π ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . ∣ S t = s ) v_π(s)=E_π(R_{t+1}+γR_{t+2}+γ^2R_{t+3}+...|S_t=s) vπ(s)=Eπ(Rt+1+γRt+2+γ2Rt+3+...∣St=s)即是在s状态和策略π时,采取行动后的价值由接下来的时刻的R的期望组成,其中γ是奖励衰减因子,用于控制当前奖励和未来奖励的比重。越小越重视现在,由于环境不可全知,未来具有更多的不确定性。
Model:用来感知场景的变化。模型要解决两个问题:一是状态转化概率 P s s ′ a P^a_{ss′} Pss′a,即预测在s状态下,采取动作a,转到下一个状态s′的概率。另一个是预测可能获得的即时奖励 R s a R_s^a Rsa。
探索率 ϵ \epsilon ϵ::即Exploration & Exploitation,强化学习类似于一个试错的学习,需要从其与环境的交互中发现一个好的策略,同时又不至于在试错的过程中丢失太多的奖励,而探索(发现新的路径)和利用(选择当前最佳)就是进行决策时需要平衡的两个方面。所以当训练时选择最优动作,会有一定的概率ϵ不选择使奖励值最大的动作,而选择其他的动作,进行那些“未知”领域的探索,说不定会有新的宝藏。
马尔科夫决策过程(Markov Decision Process,MDP)
简单说就是时刻 t 所包含的历史信息 H t = O 1 , R 1 , A 1 , . . . , O t − 1 , R t − 1 , A t − 1 , O t , R t , A t H_t=O_1,R_1,A_1,...,O_{t-1},R_{t-1},A_{t-1},O_t,R_t,A_t Ht=O1,R1,A1,...,Ot−1,Rt−1,At−1,Ot,Rt,At太长了。而环境state是历史的函数,表示目前未知已经得到了什么,接下来要继续做什么,但实际上并不需要知道所有这些历史信息。虽然不能知道环境的具体状况只能与环境进行交互,但根据马尔科夫的形式就足矣包含已经发生的所有状况。为了简化模型,那么就假设这一历史序列服从马尔科夫性。 P s s ′ a = E ( S t + 1 = s ′ ∣ S t = s , A t = a ) P_{ss'}^a = \mathbb{E}(S_{t+1}=s'|S_t=s, A_t=a) Pss′a=E(St+1=s′∣St=s,At=a)即当前的状态转移概率只与前一个状态有关。(前一个状态本身也是包含了前前一个状态,马尔科夫没问题,基本上所有的强化学习都满足MDP)
所以可以得到在状态s和策略π下的价值函数为:
v π ( s ) = E π ( R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . ∣ S t = s ) v_π(s)=E_π(R_{t+1}+γR_{t+2}+γ^2R_{t+3}+...|S_t=s) vπ(s)=Eπ(Rt+1+γRt+2+γ2Rt+3+...∣St=s) = E π ( R t + 1 + γ ( R t + 2 + γ R t + 3 + . . . ) ∣ S t = s ) =E_π(R_{t+1}+γ(R_{t+2}+γR_{t+3}+...)|St=s) =Eπ(Rt+1+γ(Rt+2+γRt+3+...)∣St=s) = E π ( R t + 1 + γ v π ( S t + 1 ) ∣ S t = s ) =E_π(R_{t+1}+γv_π(S_{t+1})|St=s) =Eπ(Rt+1+γvπ(St+1)∣St=s)
如何计算价值函数?
为了使模型训练的最好,学习到更多有用的知识即完成任务的最好策略。对策略好坏的评价标准自然是得到最多最好的奖励,那么如何找到最好的最好的奖励,即如何得到最好的价值函数?
首先对于在状态s,根据策略采取行为 a 的总奖励q是 当前奖励R 和 对未来各个可能的状态转化奖励的期望v组成,根据一定的 ϵ \epsilon ϵ 概率每次选择奖励最大q或探索,便可以组成完整的策略,那么目标就变成了计算这个 q 值,然后根据q选择策略就好。
q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a v π ( s ′ ) q_{\pi}(s,a) = R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{\pi}(s') qπ(s,a)=Rsa+γs′∈S∑Pss′avπ(s′)
- 穷举法:把所有可能的路径和状况都试一遍计算,直接比较最后哪条路的总价值最大。
- 动态规划(DP):将一个问题拆成几个子问题,分别求解这些子问题,反向推断出大问题的解。即要求最大的价值,那么根据递推关系,根据上一循环得到的价值函数来更新当前循环。但是它需要知道具体环境的转换模型,计算出实际的价值函数。相比穷举法,动态规划即考虑到了所有可能,但不完全走完。
- 蒙特卡洛(MC):采样计算。即通过对采样的多个完整的回合(如玩多次游戏直到游戏结束),在回合结束后来完成参数的计算,求平均收获的期望并对状态对动作的重复出现进行计算,最后再进行更新。 G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . γ T − t − 1 R T G_t =R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3}+... \gamma^{T-t-1}R_{T} Gt=Rt+1+γRt+2+γ2Rt+3+...γT−t−1RT N ( S t , A t ) = N ( S t , A t ) + 1 N(S_t, A_t) = N(S_t, A_t) +1 N(St,At)=N(St,At)+1状态价值函数和动作价值函数的更新就为: V ( S t ) = V ( S t ) + 1 N ( S t ) ( G t − V ( S t ) ) V(S_t) = V(S_t) + \frac{1}{N(S_t)}(G_t - V(S_t) ) V(St)=V(St)+N(St)1(Gt−V(St)) Q ( S t , A t ) = Q ( S t , A t ) + 1 N ( S t , A t ) ( G t − Q ( S t , A t ) ) Q(S_t, A_t) = Q(S_t, A_t) + \frac{1}{N(S_t, A_t)}(G_t - Q(S_t, A_t) ) Q(St,At)=Q(St,At)+N(St,At)1(Gt−Q(St,At))
这种方法是价值函数q的无偏估计,但方差高(因为需要评价每次完成单次采样的结果,波动往往很大)。 - 时序差分(TD):步步更新。不用知道全局,走一步看一步的做自身引导。即此时与下一时刻的价值函数差分(也可以理解是现实与预测值的差距)来近似代替蒙特卡洛中的完整价值。 G ( t ) = R t + 1 + γ V ( S t + 1 ) G(t) = R_{t+1} + \gamma V(S_{t+1}) G(t)=Rt+1+γV(St+1)那么: V ( S t ) = V ( S t ) + α ( G t − V ( S t ) ) V(S_t) = V(S_t) + \alpha(G_t - V(S_t) ) V(St)=V(St)+α(Gt−V(St)) Q ( S t , A t ) = Q ( S t , A t ) + α ( G t − Q ( S t , A t ) ) Q(S_t, A_t) = Q(S_t, A_t) +\alpha(G_t - Q(S_t, A_t) ) Q(St,At)=Q(St,At)+α(Gt−Q(St,At))所以它是有偏估计,但是方差小,也便于计算,在实践中往往用的最多。
Q-Learning
采用时序差分法的强化学习可以分为两类,一类是在线控制(On-policy Learning),即一直使用一个策略来更新价值函数和选择新的动作,代表就是Sarsa。而另一类是离线控制(Off-policy Learning),会使用两个控制策略,一个策略用于选择新的动作,另一个策略用于更新价值函数,代表就是Q-Learning。
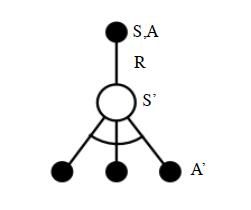
Q-Learnig的思想就是,如上图从上到下,先基于当前状态S,使用ϵ−贪婪法按一定概率选择动作A,然后得到奖励R,并更新进入新状态S′,基于状态S′,直接使用贪婪法从所有的动作中选择最优的A′(即离线选择,不是用同样的ϵ−贪婪)。 Q ( S , A ) = Q ( S , A ) + α ( R + γ max a Q ( S ′ , a ) − Q ( S , A ) ) Q(S,A) = Q(S,A) + \alpha(R+\gamma \max_aQ(S',a) - Q(S,A)) Q(S,A)=Q(S,A)+α(R+γamaxQ(S′,a)−Q(S,A))
算法流程为:

建立一个Q Table来保存状态s和将会采取的所有动作a,Q(s,a)。在每个回合中,先随机初始化第一个状态,再对回合中的每一步都先从Q Table中使用ϵ−贪婪基于当前状态 s (如果Q表没有该状态就创建s-a的行,且初始为全0)选择动作 a,执行a,然后得到新的状态s’和当前奖励r,同时更新表中Q(s,a)的值,继续循环到终点。整个算法就是一直不断更新 Q table 里的值,再根据更新值来判断要在某个 state 采取怎样的 action最好。
Sarsa
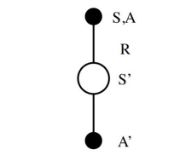
Sarsa的思想和Q-Learning类似。如上图从上到下,先基于当前状态S,使用ϵ−贪婪法按一定概率选择动作A,然后得到奖励R,并更新进入新状态S′,基于状态S′,使用ϵ−贪婪法选择A′(即在线选择,仍然使用同样的ϵ−贪婪)。 Q ( S , A ) = Q ( S , A ) + α ( R + γ Q ( S ′ , A ′ ) − Q ( S , A ) ) Q(S,A) = Q(S,A) + \alpha(R+\gamma Q(S',A') - Q(S,A)) Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))
算法流程为:

同样建立一个Q Table来保存状态s和将会采取的所有动作a,Q(s,a)。在每个回合中,先随机初始化第一个状态,再对回合中的每一步都先从Q Table中使用ϵ−贪婪基于当前状态 s (如果Q表没有该状态就创建s-a的行,且初始为全0)选择动作 a,执行a,然后得到新的状态s’和当前奖励r,同时再使用ϵ−贪婪得到在s’时的a’,直接利用a’更新表中Q(s,a)的值,继续循环到终点。
相比之下,Q-Learning是贪婪的,在更新Q时会先不执行动作只更新,然后再每次都会选max的动作,而sarsa选了什么动作来更新Q就一定执行相应的动作。这就使它不贪心一昧求最大,而是会稍稍专注不走坑,所以sarsa相对来说十分的胆小,掉进坑里面下次争取会避免它(而Q不管,每次都直接向着最小的反向学习。)不管因为Sarsa太害怕坑,而容易陷入一个小角落出不来。
on-policy与off-policy的区别
首先就判断on-policy和off-policy就在于估计时所用的策略与更新时所用的策略是否为同一个策略。比如Sarsa选了什么动作来估计Q值就一定会用什么动作来更新state,一定会执行该动作(会有贪婪率);而Q-Learning则不然,估Q值是一回事,但执行动作时一定是会选max的,即使用了两套策略,属于off-policy。
而之所以要叫on或off是因为,off-policy基本上都是要基于replay memory,即估计出的动作值肯定是最优的,但在生成策略的时候,却选择了价值最大的综合memory的max Q 的action。而on-policy每次都是选择最优的action。

放上莫大大的Q-Learning代码。
实现的是小红避免掉进黑洞最后找到小黄的故事。具体设定的reward是找到小黄得+1分,调到小黑里面-1分,其他的路都是0分。action有上下左右,环境的编写中有限制移出边界。
#this
def update():
# 学习 100 回合
for episode in range(100):
# 初始化 state 的观测值
observation = env.reset() #env是搭建的游戏环境
while True:
env.render() # 刷新可视化环境
# 根据当前s 的观测值挑选 a,观测值是环境返回,这里返回的是小红的坐标
action = RL.choose_action(str(observation))
# 执行action, 得到s', r,和终止符done
observation_, reward, done = env.step(action)
# 从这个序列 (state, action, reward, state_) 中学习
RL.learn(str(observation), action, reward, str(observation_))
# 将下一个 state 的值传到下一次循环
observation = observation_
if done:
break
# 结束游戏并关闭窗口
print('game over')
env.destroy()
#RL
import numpy as np
import pandas as pd
class QLearningTable: #关于Q表
def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
self.actions = actions #选动作,有上下左右
self.lr = learning_rate #学习率
self.gamma = reward_decay #奖励衰减
self.epsilon = e_greedy #贪婪系数
self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64) #初始Q表
def choose_action(self, observation):
self.check_state_exist(observation)#检测该状态是否存在,不存在就新建
if np.random.uniform() < self.epsilon: #随机数如果小于epsilon就选择最好的动作,如0.9的概率会选择最大
state_action = self.q_table.loc[observation, :]
# 针对同一个 state, 而不同动作的Q值却相同,采取随机选择
action = np.random.choice(state_action[state_action == np.max(state_action)].index)
else: #0.1的概率探索没有去过的地方
action = np.random.choice(self.actions)
return action
def learn(self, s, a, r, s_):#更新Q表
self.check_state_exist(s_)#检测该状态是否存在,不存在就新建
q_predict = self.q_table.loc[s, a] #得到s和动作a的Q表值,即旧值
if s_ != 'terminal': #如果游戏没有结束
#贪婪的得到最大Q值乘学习率,加上reward得到s'和a',即新值
q_target = r + self.gamma * self.q_table.loc[s_, :].max()
else:
q_target = r #如果是终点,没有后续动作,就直接是0
self.q_table.loc[s, a] += self.lr * (q_target - q_predict) # 时序差分新旧更新Q表
改一下reward把每多走一步也算进损失,即想以更少的步数找到小黄,会稍稍的快一点。
Sarsa的代码基本一样,在Q表更新的时候q_target = r + self.gamma * self.q_table.loc[s_, a_] ,即它直接选用已经确定了的a’而不是直接贪婪选max。
Sarsa lambda
把单步更新变为多步更新甚至一直到回合更新。其Lambda可以看成是步长衰减值,值域[0,1],当它为0就是普通的sarsa,为1就是一整个回合才更新一次,类似MC了。这样不仅可以对最接近结果的地方更好的更新权重,而且可以更好的更新所走过的路的权重,从而更有效率的学习。而lambda其实可以就看作是一个对远近动作的衰减值,加入到Q表的更新中。 E t ( s ) = γ λ E t − 1 ( s ) + 1 ( S t = s ) = { 0 t < k ( γ λ ) t − k t ≥ k , s . t . λ , γ ∈ [ 0 , 1 ] , s i s v i s i t e d o n c e a t t i m e k E_t(s) = \gamma\lambda E_{t-1}(s) +1(S_t=s) = \begin{cases} 0& {t
算法流程变为:

同样建立一个Q Table来保存状态s和将会采取的所有动作a,Q(s,a)。在每个回合中,先随机初始化第一个状态和动作,并执行得到奖励R和新状态S’。再从Q Table中使用ϵ−贪婪基于当前状态 s’ (如果Q表没有该状态就创建s’-a的行,且初始为全0)选择动作 a’,更新eligibility函数E(S,A)和TD差分误差δ,然后再对当前序列所有出现的状态s和对应动作a,,更新价值函数Q(s,a)和E(s,a)。