tensorflow自编码器autoencoder

参考链接：

https://morvanzhou.github.io/tutorials/machine-learning/tensorflow/5-11-A-autoencoder/  莫烦教学

自编码器

举一个形象的例子：

将一张图片打码，可以看做是压缩信息，即为编码器，此时信息量减小但都是保存的图片中的关键信息

根据打码后的图片还原到原始图片，可以看做解压缩信息，即为解码器，此时根据关键信息去还原图片

使用自解码器的原因：

神经网络要接受大量的输入信息, 比如输入信息是高清图片时, 输入信息量可能达到上千万, 让神经网络直接从上千万个信息源中学习是一件很吃力的工作.提取出原图片中的最具代表性的信息, 缩减输入信息量, 再把缩减过后的关键信息放进神经网络学习. 这样学习起来就简单轻松了. 所以, 自编码就能在这时发挥作用. 

通过将原数据白色的X 压缩, 解压 成黑色的X, 然后通过对比黑白 X ,求出预测误差, 进行反向传递, 逐步提升自编码的准确性. 训练好的自编码中间这一部分就是能总结原数据的精髓. 可以看出, 从头到尾, 我们只用到了输入数据 X, 并没有用到 X 对应的数据标签, 所以也可以说自编码是一种非监督学习. 到了真正使用自编码的时候. 通常只会用到自编码前半部分

通过autoencoder学习到数据关键信息，大大减轻了神经网络的负担，而且也达到了很好的效果，自编码器作为一种无监督学习，并不是对数据进行聚类，而是提取出最有用、最频繁的高阶特征，根据这些高阶特征去重构数据。自编码器的目标是减少重构误差。

上述的神经网络为单隐藏层的自编码器，多层隐藏层的自编码器为深度自编码器，激励函数采用多种非线性函数，压缩和解压的参数不一定对称

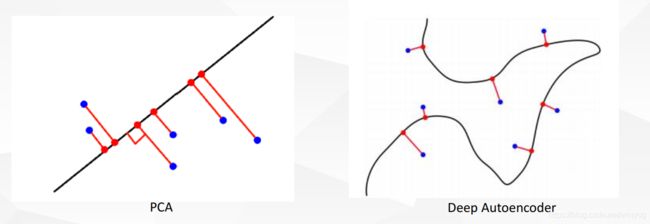
深度非线性自编码器学习如何投影数据到一个非线性流形， 而不是一个子空间，这是一种非线性的降维方式。

比较PCA， 在相同新维度下， 非线性自编码器可以学习更加有效的表示。

从下图可以看出，相比于浅层的自编码器，深层自编码器具有更好的特征提取能力，且能除去噪声信息。

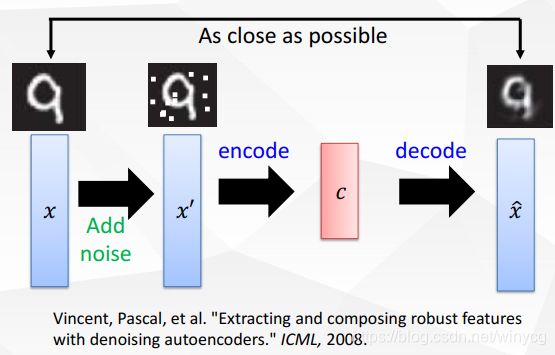
去噪自编码器

实现添加高斯噪声的去噪编码器，将自编码器封装称为一个类

我们读取后的MNIST数据集实际上就是被标准化后的数据，由原始的范围0~255标准化范围为0~1，但是在代码仍然使用sklearn库对数据进行标准化操作，并且使用random函数随机生成样本数据，用于练习对数据的预处理操作，最后对比经过自编码器后的样本

 

import tensorflow as tf
import sklearn.preprocessing as prep
import numpy as np
import input_data
import matplotlib.pyplot as plt


def xavier_init(fan_in, fan_out):
    low = -1 * np.sqrt(6.0 / (fan_in + fan_out))
    high = - low
    return tf.random_uniform((fan_in, fan_out), minval=low, maxval=high)


class AdditiveGausssianAutoencoder(object):
    def __init__(self, n_inputs, n_hiddens, activtion_function=tf.nn.softplus,
                 optimizer=tf.train.AdamOptimizer(), scale=0.1):
        self.n_input = n_inputs
        self.n_hidden = n_hiddens
        self.activtion_function = activtion_function
        self.scale = scale
        self.weights = {
            'w1': tf.Variable(xavier_init(self.n_input, self.n_hidden)),
            'w2': tf.Variable(tf.zeros([self.n_hidden, self.n_input]))
        }
        self.biases = {
            'b1': tf.zeros([self.n_hidden]),
            'b2': tf.zeros([self.n_input])
        }
        self.x = tf.placeholder(tf.float32, [None, self.n_input])
        self.hidden = tf.matmul(self.x + scale * tf.random_normal((n_inputs, )),
                                self.weights['w1']) + self.biases['b1']
        self.reconstruction = tf.matmul(self.hidden, self.weights['w2']) + self.biases['b2']
        self.loss = 0.5 * tf.reduce_sum(tf.square(self.reconstruction - self.x))
        self.optimizer = optimizer.minimize(self.loss)

        self.sess = tf.Session()
        self.sess.run(tf.global_variables_initializer())

    def partial_fit(self, X):
        loss, opt = self.sess.run([self.loss, self.optimizer],
                                  feed_dict={self.x: X})
        return loss

    def calc_cost(self, X):
        return self.sess.run(self.loss, feed_dict={self.x: X})

    def reconstruct(self, X):
        return self.sess.run(self.reconstruction, feed_dict={self.x: X})


mnist = input_data.read_data_sets('MNIST_data', one_hot=True)


def standard_scale(X_train, X_test):
    preprocessor = prep.StandardScaler().fit(X_train)
    X_train = preprocessor.transform(X_train)
    X_test = preprocessor.transform(X_test)
    return X_train, X_test


def get_random_block_from_data(data, batch_size):
    start_index = np.random.randint(0, len(data) - batch_size)
    return data[start_index: start_index + batch_size]


X_train, X_test = standard_scale(mnist.train.images, mnist.test.images)
n_samples = mnist.train.num_examples
training_epoch = 20
batch_size = 128

autoencoder = AdditiveGausssianAutoencoder(
    n_inputs=784, n_hiddens=200, activtion_function=tf.nn.softplus,
    optimizer=tf.train.AdamOptimizer(learning_rate=0.001), scale=0.01
)

for epoch in range(training_epoch):
    avg_cost = 0
    step = 1
    while step * batch_size < n_samples:
        batch_x = get_random_block_from_data(X_train, batch_size)
        cost = autoencoder.partial_fit(batch_x)
        avg_cost += cost / batch_size
        step += 1
    print('Epoch: %d' % epoch, 'cost: %.3f' % avg_cost)

print('Total cost: %0.3f' % autoencoder.calc_cost(X_test))


batch_test = get_random_block_from_data(X_test, 5)
encoder_test = autoencoder.reconstruct(batch_test)
print(type(encoder_test))
# 
fig, ax = plt.subplots(nrows=2, ncols=5)
for i in range(5):
    ax[0][i].imshow(batch_test[i].reshape((28, 28)), cmap='Greys', interpolation='nearest')
    ax[1][i].imshow(encoder_test[i].reshape((28, 28)), cmap='Greys', interpolation='nearest')
plt.tight_layout()
plt.show()