Tensorflow2.0：变分自编码器

写在前言

在网上和书上查了许多资料，关于变分自编码器的内容主要以公式推导和理论讲解为主，看了很长时间，感觉这些资料尽管在细节上讲的很清楚，但并未将变分自编码器讲透，没有说明白这个到底是什么东西，到底是干嘛用的，因此写下这篇总结，来加深对自变分编码器的认识。

VAE的核心思想

VAE认为，对于任何样本数据，可以认为是一定数量的特征组合在一起，是该组合决定了这个样本数据。对于每一个特征来说，其特征值并非固定的，是都符合正态分布概率分布，概率分布的参数也相同，且各个特征之间是相互独立的，那么只要按照该概率分布随机产生就可以产生每个特征的特征值，再把这些特征值组合到一起，就可以生成数据。这也表明，任何样本数据都是每一个特征值组成，每个特征的特征值都是一定概率才会出现的，因此特征值的组合本质就是概率的组合，样本数据的呈现本质就是概率的呈现。
当特征值的组合是以前的样本数据时，那么生成的数据就是样本数据；当特征值的组合是不是输入样本数据所对应的特征值组合时，那么生成的数据就是未曾见过的数据。以人脸数据为例，当我们输入人脸的样本数据时，VAE会学习到人脸到底是什么特征组成的，每个特征的特征值分布是怎样的，一旦学习完毕，VAE会根据每个特征值的概率分布随机生成特征，再将每个特征值组合起来就是一张人脸，当特征值组合和人脸的样本数据的特征值组合一致时，那么生成的人脸就是我们见过的，如果不一致，则是没有见过的。在理想条件下，VAE已经学到了人脸真正的特征组合时，那么就能生成我们没见过，但非常逼真的人脸了，与此同时，每个人脸的背后都会对应着一个概率。如果看明白这个思想的话，就不难理解文章结尾处那段分析，即为何VAE有时会表现效果差。

什么是自编码器？

有一个数据集{x1,x2,…xn},每个数据的呈现特点都不一样，在一般情况下，如果能出找几个特征把它形容出来，那么就可以通过这些特征构建函数来表达出数据集内任意一个数据。但现在遇到个问题，我们不知道这个数据集到底由什么特征构成，也就是说我们无法从经验上找到这个数据集的内在特质，因此便有了下面的自编码器，其结构示意图如下：

由以上结构可以得出，只要我们输入一个数据x，神经网络会前向计算出一个隐藏向量h，然后通过隐藏向量h来重构数据x，当输出的x~和x越接近的时候，说明神经网络提取出的隐藏向量h越能够代表数据集背后的特征。
但是这样的实现方式有一个缺陷，就是我们只有输入数据以后才能够获取到数据背后的隐藏向量h，因此隐藏向量h的数值范围和概率分布无法知晓，使得我们并不能从隐藏向量出发，重构一个数据。为了解决这个问题，变分自编码器就诞生了。
什么是变分自编码器(VAE)？
由上述的自编码器可知，隐藏向量h是不可控的，因此我们就想把它变成可以控制的，那么在变分自编码器中，就会对神经网络进行一定条件的约束，使得输出的隐藏向量h符合指定的分布，比如正态分布，这样我们只需要按照正态分布的概率函数随机提取一个h就能够获取一个数据，那么这个做法无疑是解决了自编码器无法提取隐藏向量h的问题。

VAE的设计思想

在自编码器中，我们衡量模型好与坏，就看输出的x~
与输入x之间的差距，希望此差距随着模型训练而减少。那么在变分自编码器中，我们模型的好与坏不光有输出的x~与输入x之间的差距，更重要的是，我们需要知道，隐藏向量h是否是符合正态分布的，为了解决这个问题，我们利用一个叫做散度KL的概念，这个KL是用来衡量两个分布之间的距离，KL值越小，则说明一个分布和另外一个分布越相似。在两个分布都是高斯分布的条件下，KL的计算比较简单，其推导和计算结果如下：

这样以来，我们模型好与坏的标准就成为了两个标准的相加，第一个标准为输出的x~
与输入x之间的差距，第二个标准为散度KL的值，那么该标准的值越小，说明我们输入x的输出的隐藏向量h的分布越会接近正态分布，根据h重构的x~和输入x越接近。那么根据上述的过程中可看出，相比于自编码器，VAE考虑隐藏向量分布与高斯分布之间的误差，使得可以在高斯分布下随机提取隐藏向量h来获取数据。从而控制了隐藏向量h的范围。

VAE的实现步骤

我们根据上述描述，做出VAE的模型结构图，然后围绕着整个结构细节来阐述VAE的实现步骤，结构图如下：

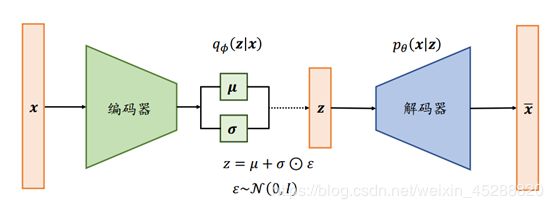
1.输入一个数据x，经过编码器，得到均值和方差

这个步骤就是在说，根据一个数据的特点，我们求出相应的q,q不是一个固定值，是一个符合均值u和方差σ的正态分布,理想条件下，q的分布就是z的分布。
解码器的作用为在数据x的条件下，求出此时隐藏向量z的概率分布，即每个特征值的概率分布，并希望该分布为正态分布。为何希望分布为正态分布？如果所有的样本数据在经过解码器下，得出每个特征值的概率分布都是正态分布的话，那么我们只需要输入一个概率分布为正态分布的隐藏向量z，就可以得到任何样本数据的特征。
2.将q进行转换，得到隐藏向量z的分布，转换公式如上图底部公式
转换是为了在求梯度的时候可导，但这个点我还是想不通为何就不可导了？
3. 输入转换后的z，经解码器，得到重构的x~

VAE为何效果差

按照我的理解，隐藏向量本质上就是一系列的特征组合，从输入x到隐藏向量，就是根据x找到x背后的特征组合，即每个特征的值。VAE认为，特征之间都是相互独立的，并且服从正态分布，基于这样的假设，可以得到一个我们可以控制的隐藏变量，从而根据这个隐藏变量生成数据。但事实上，决定事物背后的每个特征的变化规律是复杂的，特征之间不一定是相互独立，每个特征的特征值也不一定是成正态分布，因此，这种约束条件虽然能让特征组合变得可控，但并非就是事物本来的特征组合，故会产生偏差。

参考资料
1.p和q为高斯分布条件下，p和q的KL计算推导
https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians

VAE实现代码

import os
import tensorflow as tf
import numpy as np
from tensorflow import keras
from PIL import Image
from matplotlib import pyplot as plt


tf.random.set_seed(22)
np.random.seed(22)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
assert tf.__version__.startswith('2.')

# 加载MINIST数据集
(x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data()
x_train, x_test = x_train.astype(np.float32)/255., x_test.astype(np.float32)/255.


# 模型参数设定
new_im = Image.new('L', (280, 280))
image_size = 28*28
h_dim = 512
z_dim = 20
num_epochs = 55
batch_size = 100
learning_rate = 1e-3

class VAE(tf.keras.Model):
    def __init__(self):
        super(VAE, self).__init__()
        # input => h
        self.fc1 = keras.layers.Dense(h_dim)
        # h => mu and variance
        self.fc2 = keras.layers.Dense(z_dim)
        self.fc3 = keras.layers.Dense(z_dim)
        # sampled z => h
        self.fc4 = keras.layers.Dense(h_dim)
        # h => image
        self.fc5 = keras.layers.Dense(image_size)

    def encode(self, x):
        h = tf.nn.relu(self.fc1(x))
        # mu, log_variance
        return self.fc2(h), self.fc3(h)
#  猜测：根据每个样本计算出的均值和方差，针对高斯分布随机产生相应的Z向量
    def reparameterize(self, mu, log_var):
        std = tf.exp(log_var * 0.5)
        eps = tf.random.normal(std.shape)
        return mu + eps * std
# 将z进行解码
    def decode_logits(self, z):
        h = tf.nn.relu(self.fc4(z))
        return self.fc5(h)
# sigmoid激活
    def decode(self, z):
        return tf.nn.sigmoid(self.decode_logits(z))

    def call(self, inputs, training=None, mask=None):
        # encoder
        mu, log_var = self.encode(inputs)
        # sample
        z = self.reparameterize(mu, log_var)
        # decode
        x_reconstructed_logits = self.decode_logits(z)

        return x_reconstructed_logits, mu, log_var


model = VAE()
model.build(input_shape=(4, image_size))
model.summary()
optimizer = keras.optimizers.Adam(learning_rate)

# 数据预处理
dataset = tf.data.Dataset.from_tensor_slices(x_train)
dataset = dataset.shuffle(batch_size * 5).batch(batch_size)
num_batches = x_train.shape[0] // batch_size

for epoch in range(num_epochs):
    # 根据数据集训练VAE，更新参数
    for step, x in enumerate(dataset):
        x = tf.reshape(x, [-1, image_size])
        with tf.GradientTape() as tape:
            # VAE前向计算
            x_reconstruction_logits, mu, log_var = model(x)
            # 损失函数：计算重构与输入之间的sigmoid交叉熵
            reconstruction_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_reconstruction_logits)
            reconstruction_loss = tf.reduce_sum(reconstruction_loss) / batch_size
            # 计算两个高斯分布之间的散度KL 未知的为第一个高斯分布 已知N为(0,1)的分布为第二个
            kl_div = - 0.5 * tf.reduce_sum(1. + log_var - tf.square(mu) - tf.exp(log_var), axis=-1)
            kl_div = tf.reduce_mean(kl_div)
            # 损失=重构误差+分布误差
            loss = tf.reduce_mean(reconstruction_loss) + kl_div
        gradients = tape.gradient(loss, model.trainable_variables)
        # 梯度裁剪，防止梯度爆炸
        for g in gradients:
            tf.clip_by_norm(g, 15)
        optimizer.apply_gradients(zip(gradients, model.trainable_variables))
        if (step + 1) % 50 == 0:
            print("Epoch[{}/{}], Step [{}/{}], Reconst Loss: {:.4f}, KL Div: {:.4f}"
                  .format(epoch + 1, num_epochs, step + 1, num_batches, float(reconstruction_loss), float(kl_div)))

    # 计算当前参数组成的VAE下的z
    z = tf.random.normal((batch_size, z_dim))
    # 将z用sigmoid激活函数使输出在固定区间
    out = model.decode(z)
    out = tf.reshape(out, [-1, 28, 28]).numpy() * 255
    out = out.astype(np.uint8)

    index = 0
    for i in range(0, 280, 28):
        for j in range(0, 280, 28):
            im = out[index]
            im = Image.fromarray(im, mode='L')
            new_im.paste(im, (i, j))
            index += 1

    new_im.save('images/vae_sampled_epoch_%d.png' % (epoch + 1))
    plt.imshow(np.asarray(new_im))
    plt.show()

    out_logits, _, _ = model(x[:batch_size // 2])
    out = tf.nn.sigmoid(out_logits)  # out is just the logits, use sigmoid
    out = tf.reshape(out, [-1, 28, 28]).numpy() * 255

    x = tf.reshape(x[:batch_size // 2], [-1, 28, 28])

    x_concat = tf.concat([x, out], axis=0).numpy() * 255.
    x_concat = x_concat.astype(np.uint8)

    index = 0
    for i in range(0, 280, 28):
        for j in range(0, 280, 28):
            im = x_concat[index]
            im = Image.fromarray(im, mode='L')
            new_im.paste(im, (i, j))
            index += 1

    new_im.save('images/vae_reconstructed_epoch_%d.png' % (epoch + 1))
    plt.imshow(np.asarray(new_im))
    plt.show()
    print('New images saved !')