Matlab-多项式及数值微积分
08多项式和数值微积分
1.Polynomial differentiation and integration 多项式
Differentiation微分
-
例如 f(x) = x^3 -2x -5 ,用一个矩阵接收他们的系数表示一个多项式 --> p = [1 0 -2 5];
-
Plot the polynomial 给出定义域画图 for -2<=x<=5
-
polyval(多项式,定义域) 通过定义域和多项式 生成多项式函数
a = [9,-5,3,7]; x = -2:0.01:5; f = polyval(a,x); plot(x,f,'LineWidth', 2); xlabel('x'); ylabel('f(x)'); set(gca, 'FontSize', 14) -
微分:polyder(多项式) --> 返回一个新的多项式 代表原来函数的微分
-
如果要求一个点的微分
- p = [5 0 -2 0 1]; polyder§;
- polyval(polyder§,7);
-
两个多项式相乘时,两个多项式用两个矩阵接收,利用conv卷积函数进行合并
- a = [20 -7 5 10]; b = [4 12 -3]; x = -2:0.01:1
- f = conv(a,b);plot(x,f,‘Linewidth’,2);
Integration积分
- polyint(多项式,常数项) 返回一个多项式,为原函数的积分,C即为输入的常数项
2.Numerical differentiation and intetration
数值微分
-
diff() 计算单行矩阵 每个元素之间的差 (Δ)
x = [1 2 5 2 1]; diff(x) ans = 1 3 -3 -1 -
两点连线之间的斜率
x = [1 2]; y = [5 7]; %代表的不是两个点,而是两个点的x,y坐标 两个点为(1,5),(2,7) slope = diff(y)./diff(x) %y = y2 -y1 ;x = x2 - x1; -
f(x)= sinx 在 pi/2处 h=0.1的微分
x0 = pi/2; h = 0.1; x = [x0 x0+h]; y = [sin(x0) sin(x0+h)]; m = diff(y)./diff(x) -
f(x) 在(0,2π) 的微分
- 创建一个数组 x= [0,2π]
- 设置步长step 为h x=[0,0+h,0+2h,······,2π] ; f(x) = [f(0),f(0+h),f(0+2h),······,f(2π)];
- 用diff(y)./diff(x) 计算这些点的微分
-
for example:
h = 0.5; x = 0:h:2*pi; y = sin(x); m = diff(y)./diff(x);
g = colormap(lines); hold on;
for i=1:4
x = 0:power(10, -i):pi;
y = sin(x); m = diff(y)./diff(x);
plot(x(1:end-1), m, 'Color', g(i,:));
end
hold off;
set(gca, 'XLim', [0, pi/2]); set(gca, 'YLim', [0, 1.2]);
set(gca, 'FontSize', 18); set(gca, 'FontName', 'symbol');
set(gca, 'XTick', 0:pi/4:pi/2);
set(gca, 'XTickLabel', {'0', 'p/4', 'p/2'});
h = legend('h=0.1','h=0.01','h=0.001','h=0.0001');
set(h,'FontName', 'Times New Roman'); box on;
二阶微分
-
由于微分会减少一项,所以二阶微分的自变量x也应该少一个
x = -2:0.005:2; y = x.^3; m = diff(y)./diff(x); m2 = diff(m)./diff(x(1:end-1));
数值积分
柱形积分
-
h = 0.05; x = 0:h:2; midpoint = (x(1:end-1)+x(2:end))./2; y = 4*midpoint.^3; s = sum(h*y) %s 即为 4x^3从0-2的积分
梯形积分
-
h = 0.05; x = 0:h:2; y = 4*x.^3; s = h*trapz(y) -
或者
-
h = 0.05; x = 0:h:2; y = 4*x.^3; trapezoid = (y(1:end-1)+y(2:end))/2; s = h*sum(trapezoid)
辛普森Simpson规则积分
-
h = 0.05; x = 0:h:2; y = 4*x.^3; s = h/3*(y(1)+2*sum(y(3:2:end-2))+... 4*sum(y(2:2:end))+y(end))
自建函数绘制函数图像——函数指针(句柄)
写一个函数,传递函数指针和定义域作为参数,可以直接绘制函数指针指向的函数的图像。
function [y] = xy_plot(input,x)
% xy_plot receives the handle of a function
% and plots that function of x
y = input(x); plot(x,y,'r--');
xlabel('x'); ylabel('function(x)');
end
匿名函数计算数值积分——integral()函数
y = @(x) 1./(x.^3-2*x-5); %一重积分求面积
integral(y,0,2) %传参:函数指针,下限,上限
二重积分,三重积分——integral2() integral3()
f = @(x,y) y.*sin(x)+x.*cos(y); %二重积分求体积
integral2(f,pi,2*pi,0,pi) %传参: 函数指针,下限,上限,下限,上限
f = @(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)






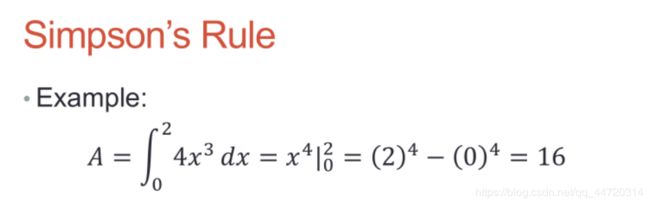
![[外链图片转存失败(img-YgwgdGFM-1567908478819)(C:\Users\46071\AppData\Roaming\Typora\typora-user-images\1566620085728.png)]](http://img.e-com-net.com/image/info8/eff7f05f461246f3b1c572b2cebf0fc3.jpg)
![[外链图片转存失败(img-US45c2Lg-1567908478819)(C:\Users\46071\AppData\Roaming\Typora\typora-user-images\1566620188777.png)]](http://img.e-com-net.com/image/info8/307c1ebd16944da7863c687bf406c3b9.jpg)
![[外链图片转存失败(img-QZ5ITLnV-1567908478820)(C:\Users\46071\AppData\Roaming\Typora\typora-user-images\1566620335520.png)]](http://img.e-com-net.com/image/info8/8958a614823e4153a490a25592f8227a.jpg)