算法与数据结构(一) -- 冒泡,插入,希尔,选择,归并,快速,堆排序
作者:opLW
参考:
- 王争老师的 《数据结构与算法之美》
- 程序员小灰的文章
- 厘米姑娘的算法面试总结
目录
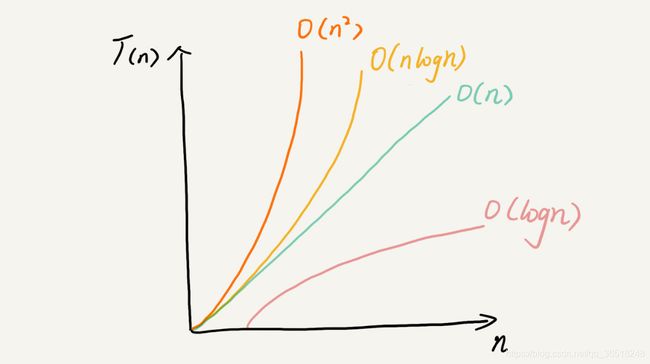
1.概览
2.冒泡排序
3.插入排序
4.希尔排序(插入排序升级版)
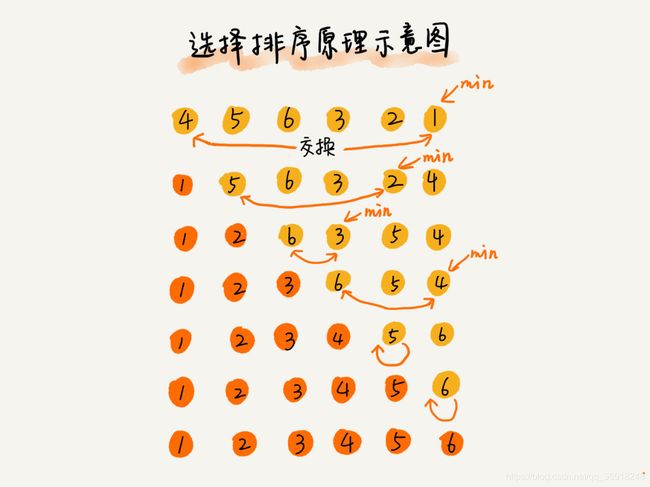
5.选择排序
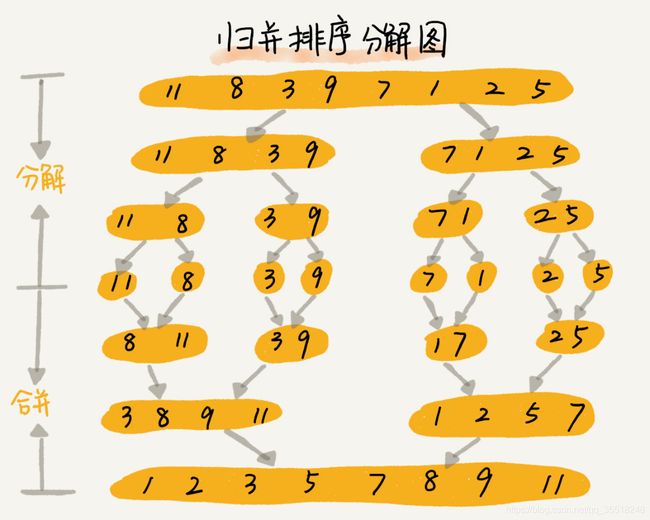
6.归并排序
7.快速排序
8.堆排序
9.快速排序,归并排序与堆排序的比较,及部分应用场景
可视化算法学习链接
1.概览
- 稳定性 针对排序算法,我们还有一个重要的度量指标,稳定性。这个概念是说,如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
例子 来解释一下。比如我们有一组数据2,9,3,4,8,3,按照大小排序之后就是2,3,3,4,8,9。这组数据里有两个3。经过某种排序算法排序之后,如果两个3的前后顺序没有改变,那我们就把这种排序算法叫作稳定的排序算法;如果前后顺序发生变化,那对应的排序算法就叫作不稳定的排序算法。
稳定排序有什么用? 在实际开发中,被比较的往往是一个对象的某一个属性,而不是单纯的数列,所以我们应该保证该属性相同的对象之间,保持排序前的顺序。比如:银行取款,我们要按用户的等级来排序,等级高的在前,与此同时我们要让等级相同的用户按先来先服务的顺序排,这个时候稳定排序的重要性就体现了。
| 名字 | 大致操作 | 时间复杂度最好/最坏/平均 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 冒泡排序 | 正如其名:从头开始至有序区,两两比较,如果前者大于后者则交换两者的位置。每一轮过后,无序区的最大值都会上浮到至末尾,从而形成有序的数列。 | O(n) / O(n^2) / O(n^2) | O(1) | 稳定 |
| 插入排序 | 从第二个元素开始,每次与前面的元素比较寻找插入的位置,每插入一个数,都会使前面的有序区增加一个数。 | O(n) / O(n^2) / O(n^2) | O(1) | 稳定 |
| 希尔排序 | 先将整个待排记录序列分割成若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次插入排序 | O(nlogn)/O(n^2)/ | O(1) | 不稳定 |
| 选择排序 | 选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。 | O(n^2) / O(n^2) / O(n^2) | O(1) | 稳定 |
| 归并排序 | 先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起。 | 复杂度稳定均为 O(nlogn) | O(n) | 稳定 |
| 快速排序 | 取一个记录作为枢轴,经过一趟排序将整段序列分为两个部分,使得数轴左侧都小于枢轴、右侧都大于枢轴;再对这两部分继续进行排序使整个序列达到有序 | O(nlogn)/O(n^2)/O(nlogn) | O(1) | 不稳定 |
| 堆排序 | 近似完全二叉树的结构,子结点的键值或索引总是小于(或大于)其父节点 | O(nlogn) | O(1) | 不稳定 |
下面仅贴出代码,便于有一定基础的同学复习。对于没有基础的同学,我也会相应的贴出详细介绍算法的链接。(来源于程序员小灰)
2.冒泡排序
public static void bubbleSort(int[] ary) {
int length = ary.length;
// 用于记录最后一个比较交换的位置
int lastExchangeIndex = ary.length - 1;
// 记录无序区的最后一个
int unsortedBorder = lastExchangeIndex;
for (int i = 0; i < length; i++) {
//记录这一次遍历是否是全部有序的,有序的话则不用再比较,直接跳出
boolean isSorted = true;
for (int j = 0; j < unsortedBorder; j++) {
if (ary[j + 1] < ary[j]) {
int tmp = ary[j];
ary[j] = ary[j + 1];
ary[j + 1] = tmp;
//有交换代表这一次遍历不是全部有序
isSorted = false;
//更新无序区的边界
lastExchangeIndex = j;
}
}
if (isSorted) {
break;
}
unsortedBorder = lastExchangeIndex;
}
}
- 两个优化
- 使用
unsortedBorder记录无序区的最后一个,减少比较的次数。 - 使用
isSorted来标记某一次遍历是否全部有序,有则直接跳出,减少比较的次数。
- 使用
3.插入排序
public static void insertSort(int[] ary) {
int length = ary.length;
//待插入的值
int insertVal;
for (int i = 1; i < length; i++) {
insertVal = ary[i];
int j = i;
//寻找插入的位置
while (j > 0 && ary[j - 1] > insertVal) {
ary[j] = ary[j - 1];
j --;
}
ary[j] = insertVal;
}
}
- 为什么最好情况下是O(n) 呢? 当数列有序时,每一个待插入的数都大于前面有序区所有的数,从而不用移动位置。
- 选择冒泡排序还是插入排序 从上面的表格可以看出,两者的时间复杂度一样,但是更多情况下,选择的还是插入排序。因为在交换无序数据次数一样的情况下,插入排序交换数据的速度更快:插入排序只需要一条赋值语句
ary[j] = ary[j - 1];,而冒泡排序需要int tmp = ary[j]; ary[j] = ary[j + 1]; ary[j + 1] = tmp;三条赋值语句。
4.希尔排序(插入排序升级版 – 跳跃式交换数据)
public static void shellSort(int[] ary) {
int length = ary.length;
int insertVal;
// 记录每一次跳跃式比较的增量
int step = length / 2;
while (step >= 1) {
for (int i = step; i < length; i += step) {
insertVal = ary[i];
int j = i;
// 注意点,与插入排序不同的是这里要">=",因为step最小为1
while (j >= step && ary[j - step] > insertVal) {
ary[j] = ary[j - step];
j -= step;
}
ary[j] = insertVal;
}
// 缩小跳跃式增量的大小为原来的一半
step /= 2;
}
}
- 希尔排序的基本思想是实现跳跃式的数据交换,而不是像直接插入排序一样一个一个的比较和移动过。在前面跳跃式交换之后,数据基本呈现有序的状态,所以最后一遍增量为1的插入排序,只要做少量的比较和交换即可完成排序。
5.选择排序
public static void selectSort(int[] ary) {
int indexOfMin;
int length = ary.length;
for (int i = 0; i < length; i ++) {
indexOfMin = i;
for (int j = i + 1; j < length; j ++) {
if (ary[j] < ary[indexOfMin]) {
indexOfMin = j;
}
}
if (indexOfMin != i) {
int t = ary[indexOfMin];
ary[indexOfMin] = ary[i];
ary[i] = t;
}
}
}
总结 以上算法比较简单,适合数量规模较小的排序。当涉及到规模大的排序时,使用以下算法较为合适。
6.归并排序
//这里的end是待排序列的最后一个元素的下标,不是我们习惯的ary.length
public static void mergeSort(int[] ary, int start, int end) {
if (start < end) {
int mid = start + (end - start) / 2;
mergeSort(ary, start, mid);
mergeSort(ary, mid + 1, end);
merge(ary, start, mid, end);
}
}
public static void merge(int[] ary, int start, int mid, int end) {
int[] tmp = new int[ary.length];
int i = start, j = mid + 1, k = start;
while (i != mid + 1 && j != end + 1) {
//决定归并排序是稳定排序的关键,当==的时候我们用的还是处于前面的数据
if (ary[i] <= ary[j]) {
tmp[k++] = ary[i++];
} else {
tmp[k++] = ary[j++];
}
}
while (i != mid + 1) {
tmp[k++] = ary[i++];
}
while (j != end + 1) {
tmp[k++] = ary[j++];
}
for (i = start; i <= end; i++) {
ary[i] = tmp[i];
}
}
7.快速排序
public static void quickSort(int[] ary, int start, int end) {
if (start < end) {
//取得中心点,中心点左边的数据小于中心点,中心点右边的数据大于中心点
int pivot = partition(ary, start, end);
quickSort(ary, start, pivot - 1);
quickSort(ary, pivot + 1, end);
}
}
public static int partition(int[] ary, int startIndex, int endIndex) {
int pivotVal = ary[startIndex];
int left = startIndex;
int right = endIndex;
while (left != right) { // ==0==
// ==1==
while (left < right && ary[right] >= pivotVal) {
right --;
}
// ==2==
while (left < right && ary[left] <= pivotVal) {
left ++;
}
if (left < right) {
int tmp = ary[left];
ary[left] = ary[right];
ary[right] = tmp;
}
}
// ==3==
int tmp2 = ary[left];
ary[left] = ary[startIndex];
ary[startIndex] = tmp2;
return left;
}
- 注意 1,2 这两个
while语句的先后顺序关系很大。看下面的示意图:
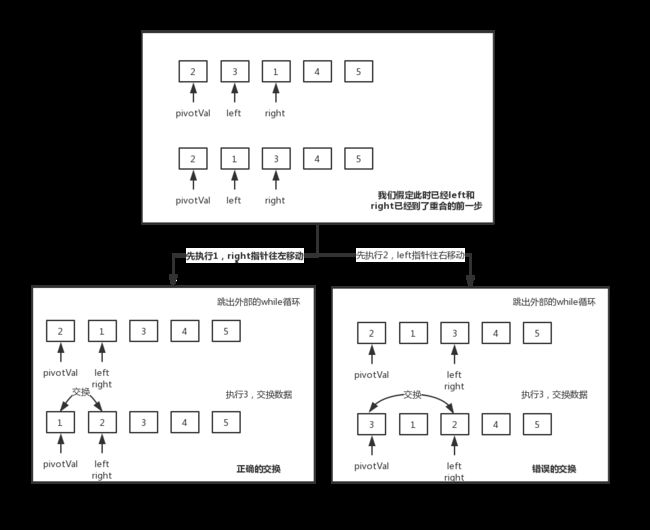
- 显而易见,区别是致命的。那为什么呢?因为我们选择的
pivotVal,其原始下标是在最左端,也就是说最后和他交换的数据应该是一个小于pivotVal的值。那么当我们先执行1时,right往左移动,重叠退出循环,此时的left指向的是比pivotVal小的值,交换正确;那么当我们先执行2时,left往右移动,重叠退出循环,此时的left指向的是比pivotVal大的值,把一个比pivotVal大的值放到pivotVal的前面显然是不行的。 总结 当我们选择最左端作为参照点时,应该先执行1,即让right指针左移;同理当我们选择最右端作为参照点时,应该先执行2,即让left指针右移。
- 显而易见,区别是致命的。那为什么呢?因为我们选择的
- 快速排序最坏的时间复杂度为O(n^2) 举一个比较极端的例子。如果数组中的数据原来已经是有序的了,比如1,3,5,6,8。如果我们每次选择最后一个元素作为pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约n次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约n/2个元素,这种情况下,快排的时间复杂度就从O(nlogn)退化成了O(n2)。
- 详细的学习链接 小灰老师的漫画算法 – 快速排序
8.堆排序
public static void heapSort(int[] ary) {
//int i = ary.length / 2 - 1 因为下标从0开始
for (int i = ary.length / 2 - 1; i >= 0; i--) {
headAdjust(ary, i, ary.length);
}
for (int i = ary.length - 1; i >= 0; i--) {
//取出大顶堆顶部的值放到后面
int tmp = ary[0];
ary[0] = ary[i];
ary[i] = tmp;
//重新调整大顶堆
headAdjust(ary, 0, i);
}
}
public static void headAdjust(int[] ary, int parent, int length) {
//取得左子节点
int child = parent * 2 + 1;
int tmp = ary[parent];
while (child < length) {
//判断左,右子节点的值谁更大
if (child + 1 < length && ary[child + 1] > ary[child]) {
child ++;
}
if(tmp > ary[child]) {
break;
}
//大于tmp的子节点的值上移
ary[parent] = ary[child];
parent = child;
child = child * 2 + 1;
}
ary[parent] = tmp;
}
- 详细的学习链接 小灰老师的漫画算法 – 堆排序
9.快速排序,归并排序与堆排序的比较,及部分应用场景
- 快速排序比归并排序常用 归并排序的时间复杂度任何情况下都是O(nlogn)而且是稳定排序,看起来非常优秀。而快速排序,正常情况下是O(nlogn),最坏情况下,时间复杂度是O(n2),但是出现的概率比较小。看起来快速排序好像由于归并排序。但是,归并排序并没有像快排那样应用广泛,这是为什么呢?因为它有一个致命的“弱点”,那就是归并排序不是原地排序算法。想象下当数据量很大的时候,归并排序会浪费很多空间。
- 快速排序比堆排序常用 堆排序不像快速排序会出现最坏情况,其时间复杂度为O(nlogn),并且不需要太多额外的空间。1.快速排序比较数据时是顺序访问,而堆排序比较数据时是跳跃式的访问,不利于cpu缓存。2.快速排序的比较和交换的次数比堆排序少,因为堆排序初始化建堆的时候可能会打乱已有的顺序,使得数组比之前无序,增加了交换的次数。
- 部分应用场景(记录一个大体的思路)
- 在大量数据中查找第k大的数据。 利用快排每一次交换之后,会以
pivot为中心,形成小于pivot和大于pivot的两部分,从而快速的排序,如果pivot + 1 == k则返回pivot对应的值。 - 在大量数据中查找前k大的数据 利用堆排序的优点,先取k个数建立一个小顶堆,然后依次遍历剩下的数据。如果比堆顶大,则替换堆顶,重新调整该小顶堆。最终小顶堆的k个数据,就是前k大的数据。
- 在大量数据中查找第k大的数据。 利用快排每一次交换之后,会以
可视化算法学习链接
- 十大经典排序算法(动画解析)
- VisuAlgo
- algorithm-visualizer
万水千山总是情,麻烦手下别留情。
如若讲得有不妥,文末留言告知我,
如若觉得还可以,收藏点赞要一起。
opLW原创七言律诗,转载请注明出处