数据结构7--二叉搜索树和二叉平衡树

二叉搜索树

1. 二叉搜索树的特点 (BST, Binary Search Tree)
   非空左子树的所有键值小于其根节点的键值
   非空右子树的所有键值大于其根系欸但的键值
   左、右子树本身也是二叉搜索树
   
2. 前序遍历
   先访问根节点，然后遍历左子树，最后遍历右子树
   
   使用递归进行遍历，访问根节点时，先打印，然后再遍历左子树和右子树
3. 后序遍历
   先遍历左子树，再遍历右子树，最后访问根节点
   
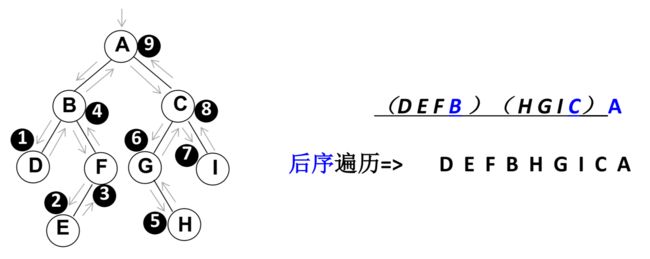
4. 中序遍历
   先遍历左子树，然后访问根节点，最后遍历右子树
   
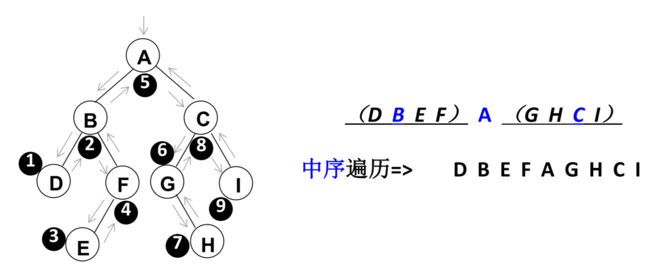
5. 删除节点
   三种情况： 要删除的节点是叶子节点 / 要删除的节点只有左子树或者只有右子树 / 要删除的节点左右子树都有

前驱：节点的左子树中的最大值
后继：节点的右子树中的最小值

//封装二叉搜索树
function BinarySearchTree(){

    this.root = null;
    //创建子树节点 拥有键值、左子树和右子树属性
    function NewNode(key){
        this.key = key;
        this.leftTree = null;
        this.rightTree = null;
    }
    this.resultString = " ";

    //插入子树
    BinarySearchTree.prototype.insert = function(key){
        let newNode = new NewNode(key);
        //如果BST为空，令要插入的子树为根节点
        if(this.root == null){
            this.root = newNode;
        }else{
            //如果BST不为空 调用insertNode
            this.insertNode(this.root,newNode)
        }
    }
    BinarySearchTree.prototype.insertNode = function(currentNode,newNode){
        //键值大小比较
        if(newNode.key < currentNode.key){ //新插入的键值比当前节点的键值小 去左子树找
            //判断当前子树是否有子树 如果没有 直接插入 有的话继续递归
            if(currentNode.leftTree == null){
                currentNode.leftTree  = newNode;
            }else{
                this.insertNode(currentNode.leftTree,newNode);
            }

        }else{
            // //新插入的子树的键值比当前子树的键值大，去右子树找
            if(currentNode.rightTree == null){
                currentNode.rightTree = newNode;
            }else{
                this.insertNode(currentNode.rightTree,newNode);
            }
        }
    }

    //查找树中的最大值和最小值
    //BST中最左边的叶子节点的键值最小 最右边的叶子节点的键值最大
    BinarySearchTree.prototype.minNode = function(){
        //如果是空树 返回false
        if(this.root == null) return false;
        let currentNode = this.root;//保存当前子树
        while(currentNode.leftTree){
            currentNode = currentNode.leftTree
        }
        return currentNode.key;
    }
    BinarySearchTree.prototype.maxNode = function(){
        //如果是空树 返回false
        if(this.root == null) return false;
        let currentNode = this.root;
        while(currentNode.rightTree){
            currentNode = currentNode.rightTree;
        }
        return currentNode.key;
    }

    //搜索指定的键值
    //找不到的两种情况：1.真的没有 2.空树
    BinarySearchTree.prototype.searchNode = function(key){
        //键值比较 向左还是向右寻找
        if(!this.root) return false;
        let currentNode = this.root;
        while(currentNode){
            if(key < currentNode.key){ //小
                currentNode = currentNode.leftTree;
            }else if(key > currentNode.key){
                //大
                currentNode = currentNode.rightTree;
            }else{ //key == currentNode.key 返回true
                return true;
            }
        }
        return false;
    }


    //前序遍历
    BinarySearchTree.prototype.preOrderTraversal = function(){
        this.preOrderTraversalNode(this.root)
    }

    BinarySearchTree.prototype.preOrderTraversalNode = function(node){
        if(node){
            console.log(node.key)
            this.preOrderTraversalNode(node.leftTree);
            this.preOrderTraversalNode(node.rightTree);
        }
    }

    //中序遍历
    BinarySearchTree.prototype.middleTraversal = function(){
        this.middleTraversalNode(this.root)
    }

    BinarySearchTree.prototype.middleTraversalNode = function(node){
        if(node){
            this.middleTraversalNode(node.leftTree);
            console.log(node.key);
            this.middleTraversalNode(node.rightTree);
        }
    }

    //后序遍历
    BinarySearchTree.prototype.backTraversal = function(){
        this.backTraversalNode(this.root)
    }

    BinarySearchTree.prototype.backTraversalNode = function(node){
        if(node){
            this.backTraversalNode(node.leftTree);
            this.backTraversalNode(node.rightTree);
            console.log(node.key);
        }
    }

    //寻找节点的后继
    BinarySearchTree.prototype.getSuccessor = function(node){
        let successorParent = node;
        let successor= node;
        let currentNode = node.rightTree;//在节点的右子树中查找
        while(currentNode){
            successorParent = successor;
            successor = currentNode;
            currentNode = currentNode.left;//找节点的右子树中的最小值
        }
        if(successor !== node.rightTree){
            successorParent.leftTree = successor.rightTree;
            successor.rightTree=node.rightTree
        }
        return successor;
    }


    //删除节点
    BinarySearchTree.prototype.delete = function(key){
        let delNode = this.searchNode(key);
        this.removeNode(delNode);
    }
    BinarySearchTree.prototype.removeNode = function (delNode) {
        let currentNode = this.root;
        let parentNode = this.root;
        let isLeftTree = true;
        //0.查找节点
        while (currentNode.key !== delNode.key){
            parentNode = currentNode;
            if(currentNode.key < delNode.key){
                //如果当前节点比要删除的节点的键值大 说明要删除的节点在当前节点的右子树上
                //继续向右子树查找
                isLeftTree = false;
                currentNode = currentNode.rightTree;
            }else {
                //说明当前节点的键值比要删除的键值大，说明要删除的节点在当前节点的左子树上
                isLeftTree =true;
                currentNode = currentNode.leftTree;
            }
            //如果currentNode指向null，说明没有找到要删除的元素
            if(currentNode.leftTree ==null && currentNode.rightTree == null) return false;
        }
        //1.情况1：要删除的节点是叶子节点
        if(delNode.leftTree == null && delNode.rightTree == null){
            //如果只有一个根节点
            if(delNode === this.root){
                this.root = null;//设置为空树
            }else if(isLeftTree){
                parentNode.leftTree = null
            }else{
                parentNode.rightTree = null
            }
        }

        //2.情况2：要删除的节点只有左子树或者只有右子树
        else if(delNode.rightTree == null){

            if(delNode == this.root){
                //如果要删除的节点是根节点，只有一个左子树
                delNode.leftTree = this.root
            }
            else if(isLeftTree){
                //要删除的节点只有子左子树 要其父节点的子树指向它的左子树
                parentNode.leftTree = delNode.leftTree
            }else{
                parentNode.rightTree - delNode.leftTree
            }
        }else if(delNode.leftTree == null){
            if(delNode == this.root){
                this.root = currentNode.rightTree
            }else if(isLeftTree){
                parentNode.leftTree = delNode.rightTree
            }else{
                parentNode.rightTree = delNode.rightTree
            }
        }
        //3.情况3.要删除的节点左右子树都有 找后继
        else{
            let successor = this.getSuccessor(delNode);
            if(this.root == delNode){
                this.root = successor;
            }else{
                if(isLeftTree){
                    parentNode.leftTree =successor;
                }else{
                    parentNode.rightTree = successor;
                }
            }
            successor.leftTree = delNode.leftTree
        }
    }
}

二叉平衡树

解决二叉搜索树中左右子节点可能存在数据不均衡的问题
非平衡二叉树的查询效率是O(N)
平衡二叉树的查找效率是O（logN）
红黑树的性质：

1. 节点是黑色和红色
2. 根节点是黑色
3. 每个叶子节点都是黑色的空节点NULL
4. 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能两个连续的红色节点）
5. 任意节点到其叶子节点的所有路径都包含相同数目的黑色节点
6. 从根到叶子节点的所有路径中，最长路径不会超过最短路径的两倍
7. 保持平衡的三种方式：变色 / 左旋转 / 右旋转