计算机中浮点数的表示
大二学的计算机组成原理,回顾下其中的知识
- 计算机中浮点数的表示
- 一个加法引发的思考
- 计算机中的原码、反码、补码、移码
- 原码
- 反码
- 补码
- 移码
- 为什么计算机中要用这些来表示数?
- 计算机中如何表示小数?
- 浮点数的转换以及加减
- 回到本文开头提出的问题
- 一些规则
- 参考文章
一个加法引发的思考
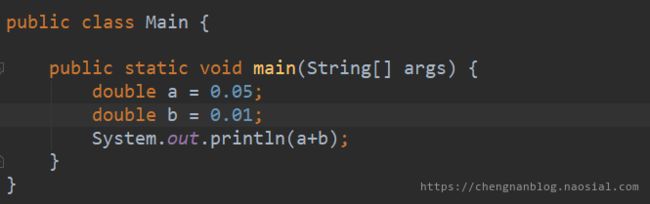
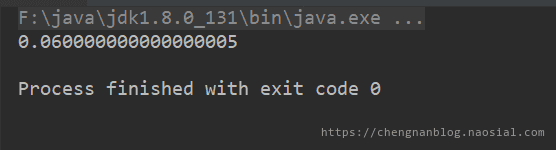
上次在一个论坛里看到了Java里的一些不正常的操作,比如说0.05+0.01的结果居然不是等于0.06,截图为证:(虽然说在学计算机组成原理的时候貌似也碰到过,但是那时并没有深入研究)
于是我便就此问题进行深入的探讨,不过却发现要计算机组成原理的相关知识,大二学的计算机组成原理,现在基本上全部还给老师了,于是重新回顾下计算机组成原理里相关的知识。
计算机中的原码、反码、补码、移码
原码
在计算机中增加了一个符号位来表示数字的正负值,符号位为0表示正数,符号位为1表示负数,是在其数值的基础上加了符号位,举个栗子:
- 123的原码为:0111 1011,第一个0表示符号位,后面的就是其二进制数值。
- -123的原码为:1111 1011,第一个1表示符号位,后面的就是其二进制数值。
早期就是用原码来表示数字的,但是这样会出问题,举个例子,假如用8位二进制数来表示一个数,那么1的原码为 0000 0001,那么-1的原码为 1000 0001,正常来说 1+(-1) = 0,但是如果用原码来进行相加的话,结果就是 1000 0010 ,用原码来表示也就是-2,和我们正确的结果不一样,这就是原码在计算上的缺点。同样用原码来表示数会出现+0和-0的情况,但是我们的0只有一个。
反码
反码也就是在原码的基础上做了一些改变,正数的反码就是其原码,负数的反码就是其原码除了符号位之后各个位取反。举个栗子:
- 123的反码为:0111 1000,也就是其原码。
- -123的反码为:1000 0111,也就是除了符号位之外,每一位取反。
补码
补码是在反码的基础上增加了一些规则,正数的补码是其本身,也就是其原码,而负数的补码也就是除符号位之外,其余各位取反,取反之后的结果加一(负数的补码相当于在其反码之后加一)。举个栗子:
- 123的补码为:0111 1000,也就是其原码。
- -123的补码为:1000 1000,也就是其反码加一。
移码
移码的计算是在补码的符号位上进行取反,举个栗子:
- 123的移码为:1111 1000。
- -123的移码为:0000 1000。
为什么计算机中要用这些来表示数?
计算机不能够像人一样直接识别10进制的数字,像1、2、3、4、5、6等,计算机中只能识别二进制的数据,所以计算机中的数据存储是以二进制为基础的,既然这样,那么就涉及到二进制数据的加减乘除,那么计算机中是如何进行处理的呢?
我们还是回到刚才讨论的1+(-1)的问题,也就是1-1的问题,如果原码表示就会出现0000 0001+1000 0001 = 1000 0010,从而得出-2的结果,这显然是不正确的,所以我们引入了反码,将二者的反码相加,0000 0001+1111 1110 = 1111 1111,然后将结果从反码转换为原码,也就是1000 0000,也就是-0,这样解决了原码减法的问题,但是还是存在问题,也就是+0和-0,在人类的认知中+0和-0是一样的,所以在计算机中也只能有一种表示。
由于反码无法解决+0和-0的问题,我们才引入补码的概念,在补码里,+0的补码为,0000 0000,-0的补码为(1000 0000)原码 ——>(1111 1111)反码 ——>(0000 0000)补码,从其反码到补码的过程由于加一之后溢出,而8位二进制数只能存储8位,所以溢出的丢弃,所以在补码里,+0,和-0的补码是一样的。
值得一提的是几个特殊数的补码,-128的补码是 1000 0000,而我们知道原码表示的时候,最高位是要用作符号位的,所以8位二进制数的原码表示范围为-(27-1)~(27-1)也就是(-127~+127),所以-128的原码是无法直接写出来的,既然这样,那-128为什么还有补码呢?
在解决上面这个问题之前,我们先来了解一下“同余定理“的概念,假如有两个数a和b,如果(a-b)能够被m整除,那么就称a和b对模m同余,这就是同余定理。现在我们回到之前,补码的提出是为了解决两个问题,第一个是计算机里的减法,将减法变成加法来做;第二个问题就是+0和-0的解决。而补码的提出就是为了让负数变成能够加的正数。这里我们举个栗子,我们知道那种挂钟是以12为单位的,如果现在是8点,我们想将其变成5点,有两种方式,第一种是顺时针拨动9格,另外一种是逆时针拨动3格。逆时针拨动3格很容易理解,就是8-3=5,而顺时针拨动9格即是8+9 = 8+(12-3) = 17=12+5。两种方式都能够得到结果,但是第一种方法采取的是化减为加的方法。
那么我们可以借鉴这样的思路来实现计算机中的减法变加法,通过以上的介绍我们很容易知道8位二进制的模为256,因为满256就进位。那么,我们来计算1+(-2)的时候,就可以计算1+(256-2)=255,而255的表示为1111 1111,刚好就是结果-1的补码((-1)——>(1000 0001)原码 ——>(1111 1110)反码 ——>(1111 1111)补码)。
那么也就是说,求一个数的补码还可以这样求,一个数的补码 = 模-这个数的绝对值。既然如此,我们就可以求-128的补码,-128的补码等于256-128,而256-128得到的结果是128,也就是(1000 0000),所以-128的补码是(1000 0000)。而我们知道,能够通过一个数的补码从而求其原码,方法是符号位不变,其他位取反,然后末尾加一,当对符号位有进位时,进位忽略(当然这是针对符号位为 1的,若符号位为0,那么原码即是补码)。既然如此那么我们根据-128的补码求其原码,(1000 0000)补码 ——>取反(1111 1111)加一(1000 0000)原码也就是说,-128的原码是-0,不过的确是这样,因为在补码里+0和-0的补码是一样的,所以选择其中一个表示0,当然+0就被选上了,那么多出的一个自然就被用作-128,所以8位二进制数的补码表示的数字要比原码和反码多一个-128。
所以我们来做一个小总结:(基于8位二进制数)
- -128的补码是[1000 0000],没有原码(根据补码求得的原码在原码看来是-0),没有反码。
- +128在8位二进制数中是没有原码、反码、补码。
- +1的原码是[0000 0001],反码是[0111 1110],补码是[0000 0001]。
- -1的原码是[1000 0001],反码是[1111 1110],补码是[1111 1111]。
- 0的原码是[0000 0000],反码是[0111 1111],补码是[0000 0000]。
计算机中如何表示小数?
在计算机组成原理这门课中我们学过,浮点数的表示有分为32位浮点数的表示和64位浮点数的表示,他们的表示方法如下图:
上面的两张图分别表示的是32位浮点数在计算机中的表示和64位浮点数在计算机中的表示,这里的阶码就类似我们使用科学计数法的指数,举个栗子,123我们用科学计数法表示为1.23×102在这里2就是阶数,而我们在利用科学计数法进行加减的时候是这样进行的,比如说1.23×102+2.556×103,我们的做法是通过移动小数点将它们的阶数变成一致,然后再进行相加。而我们通常会把小的阶数转化成大的阶数,然后再进行相加,所以转化成0.123×103+2.556×103=2.679×103。
而在计算机中同样如此,我们之前讨论过了,在计算机中是以补码的形式进行加减操作的,所以如果阶码也是用补码的话就造成了一个问题?上面我们说过我们在进行数字的相加的时候要进行对阶操作,也就是将阶数小的转化成阶数大的(这里可能有同学会问为什么不将大阶对小阶,你可以试一下,原因是大阶对小阶造成的数字丢失要比小阶对大阶要大)。那这样的话,首先要进行阶数的比较,不然怎么知道谁大谁小,如果阶码采取补码的方式,那么在一个浮点数里就有两个符号位,这样不便直接通过无逻辑的二进制进行比较,所以阶码这里不能采取有符号数,只能采取无符号数,既然这样我们为什么要用移码来表示阶码呢?
这样,我们先来提出机器零的概念,在计算机中是不能够准确的表示自然界中的0的,只能表示一个比较接近于0的数,所以在计算机中,当一个数小于计算机能够表示最小数的时候,计算机就认为这个数为0,这就是机器零,而我们知道浮点数的表示方法(32位浮点数)为(-1)S1.M×2E-127 ,其中S位符号位,M位尾数,E为阶码。所以当尾数全为0的时候不论阶码多少,这个数为0,而当阶码小于能表示的范围的最小值的时候,不论尾数为多少,这个数为0(这是因为当阶码小于能够表示范围的最小值的时候,那么整个数也就小于能够表示范围的最小值了,自然也就当0看待,那么就不用了管尾数的多少了)。
弄懂了机器零的概念,我们再回到上面讨论的用移码来表示阶码的问题。我们知道机器0在二进制的表示上是不为0的,只是在概念上为0,那么为了使机器零在表示上为0,我们引入了移码,移码在原来补码的基础上符号位取反,相当于是最高位加1,等同于整个数在原来的基础上加了2n-1其中n表示的是二进制数的位数。那也就是说在32位浮点数的里原来的数加上128就能够得到阶码了?实际上不是128而是127,那这又是什么原因呢?如果单纯的按照移码的定义,那么偏置为128能够表示的数的范围为-128~127,但是要注意0000 0000和1111 1111,这两个数分别表示非规格化数和无穷大,也就是两个边界状态,那也就是说我们实际的移码范围是0000 0001到1111 1110,也就是1到254,如果采取偏置为128那么,表示的范围是-127到126,和原来的范围相比左右各收缩一个单位,如果偏置为127,那么表示的范围是-126到127,和原来的范围相比,负数表达的范围小了,正数表达的范围没变,我们知道,在计算机中一个更大的数的表示比一个更小的数的表示要重要,所以在这里我们的偏置取127,也就是2n-1-1,那么在64位浮点数里偏置自然也就是1023了。
浮点数的转换以及加减
通过上面知识的回顾,我们来几道题目练下手,加深印象。
- (-0.75)10转化成IEEE 754单精度浮点表示
- 求 C0A00000H对应的IEEE 754单精度浮点数的值为多少?
- 计算两浮点数的和,均是10进制,0.5和-0.4375之和。(单精度浮点数)
回到本文开头提出的问题
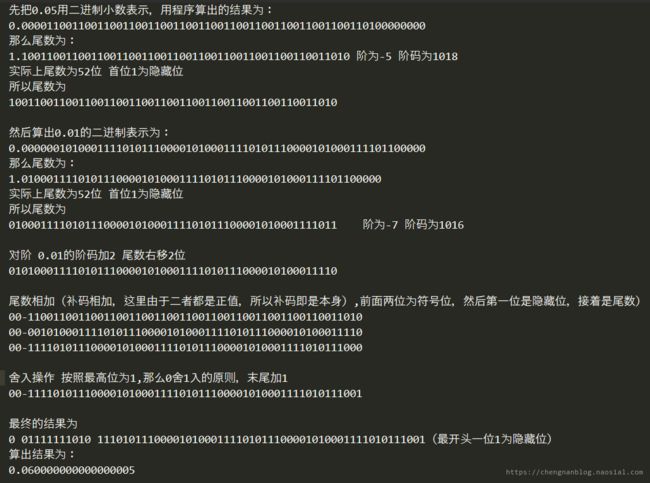
那么我们只需要将0.05和0.01分别用64为浮点数表示,之后再进行相加即可,步骤如下:
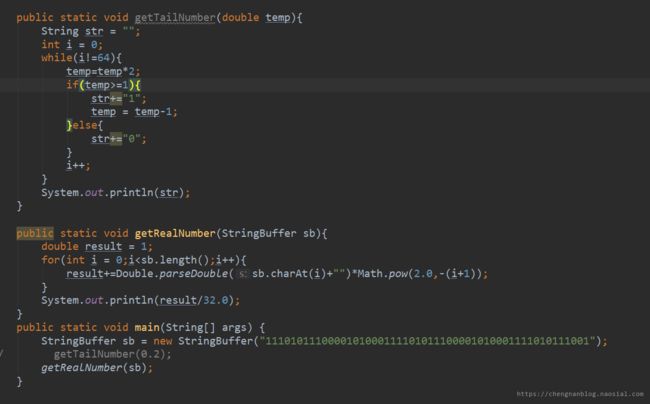
在将0.05化成二进制小数的时候采用了如下Java程序辅助计算:
在此之后笔者又找到这样的例子,并用刚才的方法进行验证,最终得出正确的结果,如下:
一些规则
- 进行浮点数加减的时候首先是对阶,对阶是小阶对大阶,小阶差大阶多少,小阶的尾数向右移多少,在右移的时候,最高位1被移出,最高位补0。
- 进行尾数相加的时候是补码相加,IEEE 754里尾数是原码表示的,所以我们要化成补码然后相加,正数的补码即其本身,负数的补码符号位不变,其它位取反,最后再加1。而且在尾数相加的时候采取的是二位符号位,00表示正数,11表示负数。(注意:这里的尾数是要包含隐藏位的)
- 当尾数相加的时候,溢出了(符号位出现01或者10的时候),当符号位为01的时候表示上溢,符号位以0为准,为正值,不过溢出之后要做右规操作,然后做舍入操作,舍入操作即是0舍1入。
- 当尾数相加,符号位为10的时候表示下溢,符号位以1为准,为负值,溢出之后做右规操作,然后做舍入操作,舍入操作即是0舍1入。
- 当尾数相加没有出现溢出的时候,此时如果最高位和符号位相同,那么需要对尾数做左规处理,直到最高位与符号位数字不同。
参考文章
细说浮点数
浮点数的加减法
浮点数的运算步骤
浮点数运算中的舍入问题
为什么说浮点数缺乏精确性,知乎陈清扬回答
【南京大学计算机组成原理】袁春风