2020 杭电多校第六场 Road To The 3rd Building（期望）

Problem Description
Because of the thriller adventure game The 3rd Building, there are fewer and fewer students who would like to go to the 3rd Building. So few students are working in the studio in the 3rd Building. Students are even more reluctant to go to the 3rd Building for experiments, which are also annoying.

Kanade takes responsibility to improve this status. She thinks it a good idea to decorate the ginkgo trees along the road to the 3rd Building, making them cute. There are n ginkgo trees that are planted along the road, numbered with 1…n. Each tree has a cute value. The cute value of tree i is si.

Kanade defines a plan as an ordered pair (i,j), here 1≤i≤j≤n. It means a student will appear at the position of the tree i magically, walk along the road, and finally stop walking at the position of the tree j. The cute level of a plan is the average of the cute value of the trees visited. Formally, the cute level of plan (i,j) is 1j−i+1∑jk=isk.

Kanade wants to know the mathematical expectation of the cute level if a student will take a plan among all these plans in a uniformly random way. But she is busy with learning Computer Networking, would you help her?

Input
The first line of the input contains an integer T — the number of testcases. You should process these testcases independently.

The first line of each testcase contains an integer n — the number of ginkgo trees.

The second line of each testcase contains n integers si — the cute value of each ginkgo tree, space-separated.

1≤T≤20,1≤n≤2×105,1≤si≤109

It is guaranteed that ∑n≤106.

Output
For each testcase, output the answer in the fraction form modulo 109+7 in one line. That is, if the answer is PQ, you should output P⋅Q−1mod(109+7), where Q−1 denotes the multiplicative inverse of Q modulo 109+7.

Sample Input
3
3
1 3 2
6
1 1 4 5 1 4
9
7325 516 56940 120670 16272 15007 337527 333184 742294

Sample Output
83333336
188888893
303405448

Hint
The answer to the first testcase is 25/12.

题意：
随机选择一个区间$[l,r]$，值为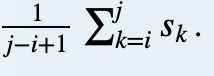

求所选区间的期望值。

思路：
假设选择的区间为长度为$2$，则当$1\le (n+1)/2$时，
其和为$\frac{a[1]+a[2]+a[3]+...+a[n-2]+a[n-1]+a[n]}{i}$

选择的区间为长度为$2$，则当$2\le (n+1)/2$时，
其和为$\frac{a[1]+a[2]\ast 2+a[3]\ast 2+...+a[n-2]\ast 2+a[n-1]\ast 2+a[n]}{i}$

区间长度为$3$的时候，当$3\le (n+1)/2$时
其和为$\frac{a[1]+a[2]\ast 2+a[3]\ast 3+...+a[n-2]\ast 3+a[n-1]\ast 2+a[n]}{i}$

于是就发现规律了。

当区间长度大于一半时候，与前一半对应的区间长度分子相同。

#include 
#include 
#include 

using namespace std;

typedef long long ll;
const int maxn = 1e6 + 7;
const int mod = 1e9 + 7;
ll a[maxn],b[maxn];
int inv[maxn];

ll qpow(ll x,ll n) {
    ll res = 1;
    while(n) {
        if(n & 1) {
            res = res * x % mod;
        }
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}

void init()
{
    inv[1] = 1;
    for(int i = 2; i < maxn; i++)
    {
        inv[i] = (ll)( mod - mod / i ) * inv[mod%i] % mod ;
    }
}

int main() {
    int T;scanf("%d",&T);
    init();
    while(T--) {
        ll n;scanf("%lld",&n);
        ll sum = 0;
        for(int i = 1;i <= n;i++) {
            scanf("%lld",&a[i]);
            sum += a[i];
        }
        sum %= mo d;
        ll frac = 0;
        ll num = (n + 1) * n / 2 % mod;
        int l = 1,r = n;
        for(int i = 1;i <= (n + 1) / 2;i++) {
            b[i] = b[i - 1] + sum;
            sum -= a[l] + a[r];
            l++;r--;
            b[i] %= mod;
        }
        for(int i = 1;i <= (n + 1) / 2;i++) {
            frac += b[i] * inv[i] % mod;
            frac %= mod;
        }
        for(int i = n;i > (n + 1) / 2;i--) {
            int pos = n - i + 1;
            frac += b[pos] * inv[i] % mod;
            frac %= mod;
        }
        frac = ((frac % mod) + mod) % mod;
        printf("%lld\n",frac * qpow(num,mod - 2) % mod);
    }
    return 0;
}