点分治与点分树学习

关于树链分治的一些东西

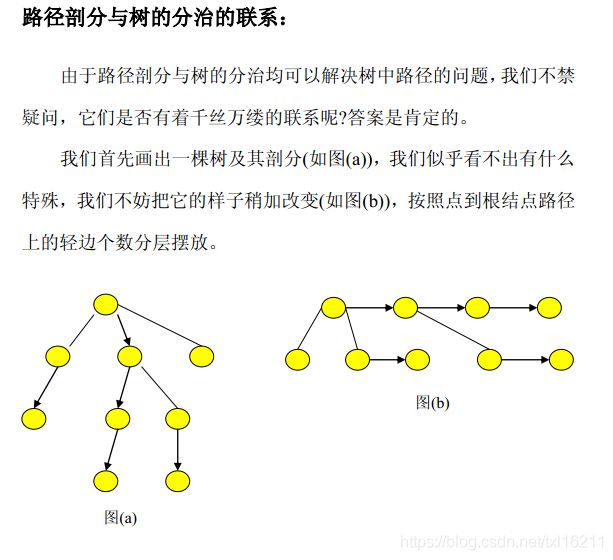
《分治算法在树的路径问题中的应用》

例题
给出一棵n个结点的有根树，每个结点有颜色。

有若干询问，询问有多少种颜色，在v为根的子树中至少有k个结点属于该颜色。

算法1
莫队（好像都是这么叫的）离线方法。时间复杂度$O(n\sqrt{n})$。

算法2
这个算法基于一个简单的结论：每个询问的答案不会超过$n/k$。这样，我们确定一个阀值x=$\sqrt{n}$，当k≤x时的答案可以预处理出来，如果k>x，我们也要预处理，不过对于每个点，数量大于x的颜色最多只有$n/x$个，不会太多。
这样的时间复杂度是$O(n\sqrt{n})$的，是一个在线算法。

算法3
离线算法，启发式合并，时间复杂度$O(n(logn{)}^2)$。

算法4 重点
假设现在树退化成了链，你会怎么做呢？
当然是开两个数组，num[i]表示i颜色出现的次数，cnt[i]表示k=i时的答案。这样，我们从链尾到链头扫一遍就可以O(n)解决了。

现在是树，我们先把它剖成若干条链（其实是小于logn条），然后对于一条链，同样采用上面的方法，只不过有个问题，这条链上可能带有若干其他的链（如图），这样对于长度为m的链，我们统计的复杂度并不是O(m)的。

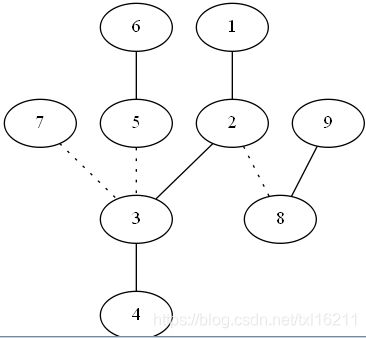
1 2 3 4 这条链就连着一些其他链。

其实，我们直接暴力统计其他的链，由于每个点到根最多只会遇到logn条链，所以每个点只会被拿去统计logn次。所以我们得到一个漂亮而简洁的算法，时间复杂度O(nlogn)。
估计代码非常短，速度非常快！

Part A.点分治

众所周知，树上分治算法有$3$种：点分治、边分治、链分治（最后一个似乎就是树链剖分），它们名字的不同是由于分治方式的不同的。点分治，顾名思义，每一次选择一个点进行分治，对于树上路径统计类型的问题有奇效，思路很好理解，只是码量有些烦人

先来看一道模板题：CF161D

至于为什么我没有放Luogu模板题是因为那道题只会写$O(n^{2}logn)$的算法（然而跑得过是因为跑不满）

这道题要求在$N$个点的树上找距离为$K$的点对的数量。

因为我们是来学点分治的，所以我们考虑点分治。我们每一次选择一个分治中心，那么以这一个分治中心为根，这棵树就会有若干子树。这棵树上的路径被分为了两种：

①经过分治中心

②没有经过分治中心，也就是说这条路径在以当前分治中心为根的一棵子树内

我们可以递归解决②对应的问题，也就是说我们只要解决当前树的①问题。

考虑每一次选择一棵子树对其进行深度优先搜索，开一个桶记录之前经过的子树中每一种路径长度对应的路径数量（一个小注明：路径指的是当前分治中心到达子树中某一个点的路径，下同）。每一次找到一条长度为$L$的路径之后，它对答案的贡献就是之前搜索过的子树中长度为$K-L$的路径的数量，因为这一条路径可以与这一些路径中的每一条拼接形成长度为$K$且经过当前分治中心的路径。在一棵子树遍历完了之后，再将这一棵子树的路径放入桶内。注意：不能找到一条路径就放进桶里面，因为这样可能会导致同一棵子树的两条路径被拼接并计入答案，但实际上它们之间的树上路径属于②，不应该在当前分治中心被统计到。当前分治中心解决之后，清空桶中元素，分治解决以当前分治中心为根的子树上的路径。

当然，你会发现一个问题：如果给出了一条链，结果你每一次选择的分治中心都是链两端的点，那复杂度不轻松卡成$O(n^2)$？？？

然而智慧的你不会让出题人这么轻松地卡掉你，我们考虑每一次选择一个点，以它为根时，子树大小尽量平均，也就是说最大的子树要尽量的小

那么我们当然会选择——树的重心！

因为树的重心的优雅性质（以它为根的子树的大小不超过当前树大小的$\frac{1}{2}$），我们每一次分治下去的子树的大小都至少会减半，也就保证了$O(nlogn)$的复杂度。

再来一题：Tree

咦这题的等于$K$怎么变成小于等于$K$了

那么我们就不能使用桶了。而使用线段树等数据结构码量又会增大不少，我们可不可以用更优秀的方法解决呢？当然有。

每一次分治时，我们考虑将路径存下来，并按照长度从小到大排序，然后使用两个指针$L,R$来扫描路径数组并获取答案。

可以知道，当$L$在不断向右移动的时候，满足$le{n}_L+le{n}_R\le K$的最大的$R$是单调递减的，所以可以直接调整$R$满足要求。调整了$R$之后，那么我们的答案就是$R-L$…

等等，我们没有考虑同一子树，所以我们还需要存下每一条路径的来源是哪一棵子树，用桶存好$L+1$到$R$之间每一个来源的数量，每一次$L$和$R$移动的时候维护这个桶，那么实际贡献的答案就是$R-L-\text{L+1到R中与L来源相同的路径的数量}$。

我们每一次分治的复杂度就是$O(\text{分治区域大小}log\text{分治区域大小})$的，总复杂度是$O(nlo{g}^{2}n)$。如果写基数排序之类的东西的话复杂度就是$O(nlogn)$

然后放几道练习题：

基础（比较裸就没有讲什么了）：

Luogu点分治模板

点分治模板
聪聪可可

聪聪可可
Race

Race
较难：（Solution更新中）

快递员 Sol

树的难题 Sol

树上游戏

重建计划 Sol

B.动态点分治（点分树）

什么？点分治还能带修改？Of course!

我们可以发现：根据点分治，我们可以构建出一棵树，在点分治过程中，如果从$solve(a)$递归到了$solve(b)$，就令$a$所在分治区域的重心为$b$所在分治区域重心的父亲，这样我们就可以构造出点分树。点分树有几个优美的性质：

$a.$点分树的高度不超过$O(logn)$，因为点分治的递归深度不会超过$logn$

$b.$点分树上某个点的祖先（包括它自己）在点分治时的分治范围必定包括了这个点，而其他点的分治范围一定不会包含这个点。

$c.$点分树上某个点的儿子一定在这一个点的分治范围的子树中（废话）

这个性质告诉我们：如果在点分树上进行修改，只需要修改它到根的一条链，修改点数不会多于$logn$。

具体来说，看一道题：捉迷藏 ； 加强版：Qtree4

我们就说$Qtree4$的做法吧，毕竟捉迷藏是边权为$1$的特殊版本。

我们构建好点分树，考虑如何在点分树上维护答案。我们需要支持插入、删除和查询最大值、次大值，考虑使用堆+懒惰堆思想进行维护。

我们对每一个点维护一个堆$heap1$，维护当前节点对应的分治范围内的路径的最大值和次大值。但我们又会面对与静态点分治一样的问题：可能来自当前节点的同一个子树的一条路径在当前节点贡献答案。所以我们对于每一个节点还要维护当前节点对应的分治范围内的路径到达当前节点在点分树上的父亲的路径长度的堆$heap2$，这样父亲在转移时就可以直接取它的所有儿子的$heap2$的最大值放入自己对应的$heap1$中，统计答案的时候把它的$heap2$的最大值从它的父亲的$heap1$中删掉，就可以避免了重复的计算。然后我们在全局维护一个堆$heap3$来维护全局的答案，每一次产生新的答案就进行维护。

那么我们每一次翻转一个节点的颜色的时候，就在点分树上暴跳父亲，并维护好$heap1,heap2,heap3$。初始化的时候也暴跳父亲。复杂度$O(nlo{g}^{2}n)$，在$Qtree4$上有一些卡常，给出一种优化方式：在删除的时候，不要在懒惰堆中加入一个元素就尝试删除答案堆，而是在询问的时候进行，这样可以降低常数。

注意一个细节：如果某一个节点可以被计入路径中，在它对应的$heap2$中是需要插入两个$0$的（表示自己与自己匹配或者自己与儿子匹配），这样子的答案才是正确的。