《白话强化学习与PyTorch》学习笔记---第八章

该部分完整代码在此：https://github.com/catziyan/DRLPytorch-/tree/master/08

1. 概述

第八章用了nips-DQN、nature-DQN、double-DQN、dueling DQN四种算法来训练Gym中的atari游戏—pong，就是控制球拍与电脑玩乒乓球，电脑丢球，reward为1；（自己）丢球，reward为-1；其余reward为0。某一方获得21分后游戏结束，done为True。游戏很简单，单作为小白初学就上手atari游戏，还是很折腾。先说说这本书在这一章中的一些坑，希望能给正在或则将要学习这本书的小伙伴一点帮助，其余朋友可以跳过这一部分。

1. 书中提供的这一章的代码可以说是一个都不能用，主要原因是对环境没有任何处理且输入神经网络的图片为单帧图片，这样无法判断乒乓球的运动方向，其次对图片的处理有问题，因threshold中的阈值选择的不对而导致处理后的图片为全白（值全都为255，这怎么可能训练出来呢…），最后探索率每次更新下降太慢，书中代码要1000000个回合探索率才能从1.0降到0.1，而我国庆运行七天才训练了3000个回合，并且综上可想而知训练结果很糟糕。
2. 书中202页中Double DQN 的伪代码及讲解错误，要学习的朋友注意不要被误导，具体可以参考刘建平老师的文章或则原论文（Deep Reinforcement Learning with Double Q-learning）

PS:因为本书是今天9月份才出版…一些印刷错误和不足在所难免，书还是很有学习价值的…

2. Pong环境选择及处理

在gym的官方网站中能够找到两款关于pong的游戏介绍，一个是Pong-ram-v0（观察到的是Atari机器的RAM，包含128个字节）另一个是Pong-v0（观察结果为RGB图像，大小为（210，160，3))，一般选择以图像作为神经网络的输入，下图为官方介绍：

翻译过来为：训练目的是使得分最大化。在这个环境中的观察结果(observation)是RGB图像，大小为（210，160，3），在2~4（随机采样）帧内重复同一个动作。

最开始看环境介绍并没有发现问题，直接用该环境进行训练，结果训练结果并不理想，后面参考这篇博客发现了问题所在：

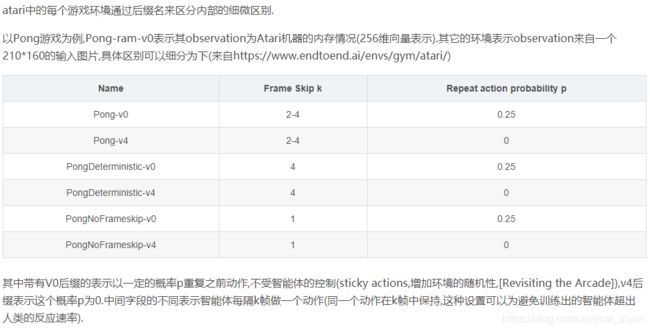
可以看出若使用Pong-v0进行训练将存在两个不确定性：

1. Frame Skip k是随机的（这样会使得状态空间增加，增加了训练难度）
2. 会有0.25的概率不执行智能体这次输出的动作，保持上一回的动作（训练时已经设置了探索率，所以并不希望有这个概率存在…）

所以要么需要对Pong-v0环境重新经行更改封装（网上很多都是写一个wrappers），要么选择一个合适的环境，对于小白的我来说，还要研究环境封装也太难了（┭┮﹏┭┮），故我分别用了PongDeterministic-v4和PongNoFrameskip-v4进行训练，都可。其中PongDeterministic-v4在博客所提到的网站（https://www.endtoend.ai/envs/gym/atari/）写到：Deterministic-v4 is the configuration used to assess Deep Q-Networks.所以该环境为首选，其次PongNoFrameskip-v4可以手动写代码进行跳帧处理，同样简单可行。

ps：我们认为这个游戏只能有向上或者向下两个动作，但在研究过程中，打印env.action_space.n的结果为6，这是由于这款atari游戏环境中设定当action为0和1的时候球拍不动，为2和4的时候球拍向上运动，为3和5的时候向下运动。

3. 图片处理

图片处理主要分为两个部分—压缩为灰度图和将连续四帧堆叠在一起,在util.py文件中

def preprocess(observation):
    img = np.reshape(observation,[210,160,3]).astype(np.float32)
    # RGB转换成灰度图像的一个常用公式是：ray = R*0.299 + G*0.587 + B*0.114
    img = img[:, :, 0] * 0.299 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114   #shape (210,160)
    resized_screen = cv2.resize(img, (84, 110), interpolation=cv2.INTER_AREA)  # shape(110,84)
    x_t = resized_screen[18:102,:]
    x_t = np.reshape(x_t,[84,84,1])
    x_t.astype((np.uint8))
    x_t = np.moveaxis(x_t, 2, 0)  #shape（1，84，84）
    return np.array(x_t).astype(np.float32) / 255.0

采用论文Playing Atari with Deep Reinforcement Learning所提到的卷积神经网络架构

需要注意几点：

1. cv2.resize(image, (width(列), height(行))) 是将图片进行压缩操作，第一个参数为列，第二个参数为行，所以压缩完后为(110,84)
2. 还可以用cv2.cvtColor(image, cv2.COLOR_BGR2GRAY) 将图片转换成灰度图（值会有所不同），此时已将图片的大小从三维转换成二维。
3. x_t = resized_screen[18:102,:]为截取压缩后的图片，去掉图片上方比分信息及上边界和下边界这些无用信息
   最初的图片和处理后的图片对比如下
   
   

叠加操作：将连续的进过处理后的四帧图片叠在一起作为神经网络的输入，（不要与跳帧搞混了，这里是连续的四个observation），大小为（4，84，84）

1. 先将初始化后状态重复4下存入state_shadow里

    state = env.reset()
    state = preprocess(state)
    state = np.reshape(state, (84, 84))
    state_shadow = np.stack((state,state,state,state),axis=0)
   

2. 每次得到一个新的next_state，再和原state_shadow里的后3个状态一起组成一个新的next_state_shadow

    next_state, reward, done, info = env.step(action)
    reward_real = reward
    next_state = preprocess(next_state)
    next_state_shadow = np.append( next_state, state_shadow[:3,:,:],axis=0)
   

4. 网络架构

参考论文Playing Atari with Deep Reinforcement Learning中的架构，两个卷积层加一个全连接层，如下图所示。神经网络的学习可以参考我的上一篇读书笔记，《白话强化学习与PyTorch》学习笔记—第六章

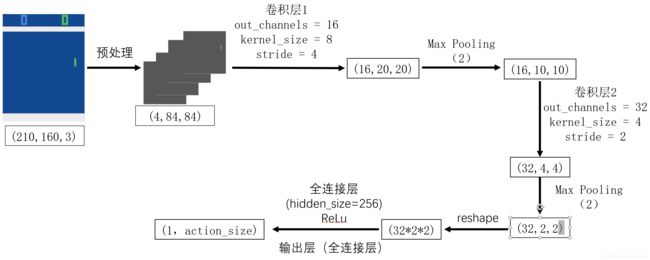
所对应的代码部分在net.py文件里，如下：

class CnnDQN(nn.Module):
    def __init__(self, inputs_shape, num_actions):
        super(CnnDQN, self).__init__()

    self.inut_shape = inputs_shape
    self.num_actions = num_actions

    self.features = nn.Sequential(
        nn.Conv2d(inputs_shape[0], 16, kernel_size=8, stride=4),
        nn.MaxPool2d(2),
        nn.Conv2d(16, 32, kernel_size=4, stride=2),
        nn.MaxPool2d(2),

    )

    self.fc = nn.Sequential(
        nn.Linear(self.features_size(), 256),
        nn.ReLU(),
        nn.Linear(256, self.num_actions)
    )

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

    def features_size(self):
        return self.features(torch.zeros(1, *self.inut_shape)).view(1, -1).size(1)

5. DQN算法族

关于DQN算法原理介绍的有很，详细可以看刘建平老师的博客，写的非常好！（感觉我已经变成了他的小迷妹）这里我只是简单介绍一下算法流程，因为我提供的代码是将这几种算法写在了一个.py文件中（略微有点混乱），所以简单介绍一下程序里对应的代码实现。

nips-dqn

nips-dqn是在2013年出现的最早的dqn算法，它将传统的强化学习算法q-learning与神经网络相结合，将状态向量作为神经网络的输入，输出得到相应状态每一个动作的价值，DQN解决了高维训练的问题，算法实现流程如下：

初始化经验回放集合$D$及容量$N$
初始化$Q$网络
for $episode=1,M$ do (一个$episode$就代表该游戏中有一方得了21分)
     初始化环境状态,得到环境的第一个状态$s_1$,将其处理为状态向量${\varphi }_1$（即图像处理过程，处理为神经网络的输入）;
     for $t=1,T$ do
          以$ϵ$的概率选择一个随机动作$a_t$，否则选择 $a_t=ma{x}_a{Q}^{\ast }(\varphi (s_t),a;\theta )$
          在环境中执行动作$a_t$并且得到奖励值$r_t$和下一时刻的状态$s_{t+1}$,以及是否为终止状态$done$
          将状态$s_{t+1}$处理为状态向量${\varphi }_{t+1}$
          将（${\varphi }_t,a_t,r_t,{\varphi }_{t+1},done$）这五个元素存入经验回访集合$D$
          从$D$中随机采样$minibatch(m)$个样本，用来计算目标$Q$值$y_j$
          $$y_j=\{\begin{array}{ll}{R}_j& \text{done=True}\\ R_j+\gamma ma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime };\theta )& \text{done=False}\end{array}$$
          使用均方差损失函数$\frac{1}{m}{\sum }_{j=1}^m(y_j-Q({\varphi }_j,a_j;\theta ))$更新神经网络参数
          如果$done=True$，跳出本循环，进行下一个$episode$

在DQN.py文件中，在Class agent中的learn函数中：

    # dqn
     next_q = self.tar_net(next_state).detach()
     target_q = reward + GAMMA * next_q.max(1)[0].view(BATCH_SIZE, 1) * done

这里就是对目标$Q$值的计算，其中当算法中的$done=True$时，此时程序中的$done=0$
在class agent中定义了两个网络，一个是self.network，一个是self.tar_net，可以发现2013版算法只有一个$Q$网络,所以需要将超参数UPDATA_FREQUENCY设置为1，这样self.network=self.tar_net（具体会在nature-dqn部分讲到）
以上就是nips-DQN的整个算法流程，下面的都是在该DQN算法上的变型

nature-dqn

2015年出现的nature-dqn相比于2013版的dqn有一次重大的改造，就是将一个网络变成了二个网络，出现了主网络和目标网络的概念，可以先看一下算法流程，与2013版不一样的地方下面将标记成红色

初始化经验回放集合$D$及容量$N$
初始化当前$Q$网络参数$w$,目标$Q$网络参数$w^{\prime }$,网络参数$w=w^{\prime }$，目标网络更新频率$C$
for $episode=1,M$ do (一个$episode$就代表该游戏中有一方得了21分)
     初始化环境状态,得到环境的第一个状态$s_1$,将其处理为状态向量${\varphi }_1$（即图像处理过程，处理为神经网络的输入）;
     for $t=1,T$ do
          以$ϵ$的概率选择一个随机动作$a_t$，否则选择 $a_t=ma{x}_a{Q}^{\ast }(\varphi (s_t),a;\theta )$
          在环境中执行动作$a_t$并且得到奖励值$r_t$和下一时刻的状态$s_{t+1}$,以及是否为终止状态$done$
          将状态$s_{t+1}$处理为状态向量${\varphi }_{t+1}$
          将（${\varphi }_t,a_t,r_t,{\varphi }_{t+1},done$）这五个元素存入经验回访集合$D$
          从$D$中随机采样$minibatch(m)$个样本，用来计算目标$Q$值$y_j$
          $$y_j=\{\begin{array}{ll}{R}_j& \text{done=True}\\ R_j+\gamma ma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime },{\theta }^{\prime })& \text{done=False}\end{array}$$
          （注意：计算$y_i$的网络参数为${\theta }^{\prime }$，即使用的是目标$Q$网络）
          使用均方差损失函数$\frac{1}{m}{\sum }_{j=1}^m(y_j-Q({\varphi }_j,a_j;\theta ))$更新当前神经网络参数$w$
          如果$T/C=1$,更新目标网络参数$w^{\prime }$
          如果$done=True$，跳出本循环，进行下一个$episode$

可以看出，nature-dqn就是新增加一个目标网络来计算目标$Q$值$y_i$，若$C=1$,则就变为2013版dqn。可以看出，nature-dqn减少了目标$Q$值计算和主网络之间的依赖关系，可以使主网络收敛平稳一些。

看到这儿大家应该就会恍然大悟，上面提到的超参数UPDATA_FREQUENCY就是算法中的$C$,因此程序中要实现nips-dqn和nature-dqn的切换只需要改变UPDATA_FREQUENCY，我设置的为1000

double-dqn

double-dqn是在nature-dqn的基础上做了进一步改变，它同样有两个$Q$网络，但计算目标$Q$值$y_i$有所不同（当$done=False$不同）。
nature-dqn计算$Q$值的式子为：
$$R_j+\gamma ma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime },{\theta }^{\prime })$$
即当前时刻的奖励$R_j$加上$\gamma$乘以 在目标$Q$网络(${\theta }^{\prime }$)中 的下一时刻的状态 所对应的所有动作$Q$值中的最大值。
而double-dqn计算$Q$值的式子为：
$$R_j+\gamma Q^{\prime }({\varphi }_{j+1},argma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime },\theta ),{\theta }^{\prime })$$
看着是要复杂了一些，可以分为两步来看，$argma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime },\theta )$为在当前网络($\theta$)中找到下一时刻最大$Q$值所对应的动作($a^{\prime }$)，然后在目标网络(${\theta }^{\prime }$)中计算下一时刻，动作($a^{\prime }$)所对应的目标$Q$值。
除了上述计算$y_i$与nature-dqn有所不同，其余都一样，故就不在写算法流程了，直接看代码：

    # dqn
    # next_q = self.tar_net(next_state).detach()
    # target_q = reward + GAMMA * next_q.max(1)[0].view(BATCH_SIZE, 1) * done
    
    ## double-dqn
    actions_value = self.network.forward(next_state)
    next_action = torch.unsqueeze(torch.max(actions_value, 1)[1], 1)
    next_q = self.tar_net.forward(next_state).gather(1, next_action)
    target_q = reward + GAMMA * next_q * done

上面注释的部分是刚才的nature-dqn，下面是double-dqn，是不是double-dqn也没有多几行代码咧。代码就是上述公式的实现，就不再赘述了，double-dqn的优势为在一定程度上降低了发生过估计的可能性。

dueling-dqn

前面两种都是对算法的优化，dueling-dqn是对神经网络的优化，之前的神经网络都是输入当前的状态，就直接得到当前状态所有动作所对应的$Q$值，而dueling-dqn将网络分为了两个部分，先看一下论文中的网络结构对比图：

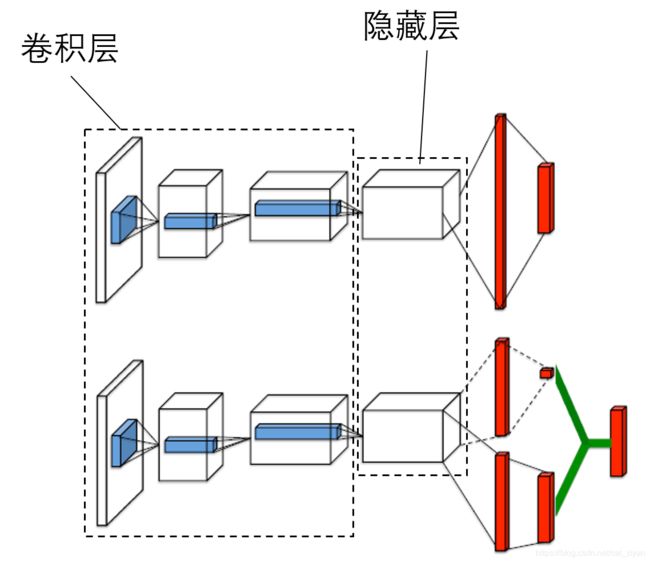
可以看出，dueling-dqn在隐藏层之后将网络分为了两个部分，前面的网络是共享的(网络参数为$w$)，后面的网络则各有各的待定系数，其中一个是价值函数$V(S;w,\alpha )$，它只与当前时刻的状态有关，故输出大小为1，网络系数为($\alpha$)；另一个是优势函数$A(S,a;w,\beta )$，它不仅与当前时刻的状态有关，还与动作有关，故输出大小为动作个数(action_size)，其网络系数为($\beta )$。最后为了辨识最终输出里面价值函数和优势函数各自所起的作用，对优势函数部分做了中心化处理，有两种处理形式，最终$Q$网络的输出为下式：
$$Q(S,a;w,\alpha ,\beta )=V(S;w,\alpha )+(A(S,a;w,\beta )-\frac{1}{|A|}\sum _{a^{\prime }}A(S,a^{\prime };w,\beta ))$$
$$Q(S,a;w,\alpha ,\beta )=V(S;w,\alpha )+(A(S,a;w,\beta )-ma{x}_{a^{\prime }\in |A|}A(S,a^{\prime };w,\beta ))$$
因为dueling-dqn是对网络结构的优化，故现有的DQN算法可以在使用Duel DQN网络结构的基础上继续使用现有的算法。由于算法主流程和其他算法没有差异，这里就不讲算法流程了，直接看代码：

class DuelingNet(nn.Module):
    def __init__(self, inputs_shape, num_actions):
        super(DuelingNet, self).__init__()
        self.input_shape = inputs_shape
        self.num_actions = num_actions
        self.features = nn.Sequential(
            nn.Conv2d(inputs_shape[0], 16, kernel_size=8, stride=4),
            nn.MaxPool2d(2),
            nn.Conv2d(16,32,kernel_size=4, stride=2),
            nn.MaxPool2d(2)
        )
        self.hidden = nn.Sequential(
            nn.Linear(self.features_size(), 256, bias=True),
            nn.ReLU()
        )

    self.adv = nn.Linear(256, num_actions, bias=True)
    self.val = nn.Linear(256, 1, bias=True)

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size(0), -1)
        x = self.hidden(x)
        adv = self.adv(x)
        val = self.val(x).expand(x.size(0),self.num_actions) #扩展某个size为1的维度，值一样  （1，6）
        x = val + adv -adv.mean(1).unsqueeze(1).expand(x.size(0),self.num_actions)
        return x

    def features_size(self):
        return self.features(torch.zeros(1, *self.input_shape)).view(1, -1).size(1)

可以看出它与上面网络结构的代码部分不同点在于多了两个self.adv和self.val线性输出层，最后的输出x为adv和val的线性组合。
dueling-dqn使用了一种比较巧妙的方式将动作本身和状态本身的价值解耦。书里有段话对dueling-dqn的理解特别生动形象：在评估下棋的策略时——有的盘面本身价值很高，也就是说，眼看就要赢了，走哪一步都差不多；有的盘面一般，状态胶着，局势不明朗，但是一些步子走出来价值就很高，步子与步子之间的估值差异比较大。这种解耦的假设，也会帮助网络学到更为准确的状态价值估值，从而更有效的找到好的策略。

6. 仿真分析

后面的仿真分析主要是为了解决我一个疑惑。
前面讲到该游戏当某一方得分21分时，环境输出的done才为True，即改状态的Q值计算采用$y_j=R_j$：
程序中体现在将那五个元素存入经验回放集合$D$中时的操作：

    if done:
        self.memory.append((state, action, reward, next_state, 0))
    else:
        self.memory.append((state, action, reward, next_state, 1))

即若done=True，则存入0，待会儿计算的时候乘以0，就只剩下$y_j=R_j$了。

但是是否可以将某一方丢球后，done就等于True呢？因为此刻该状态理论上也可以看做是中止状态（因为新的一次发球将开始） ，即当|reward|=1时，就存入0：

    if reward==0:
        self.memory.append((state, action, reward, next_state, 1))
    else:
        self.memory.append((state, action, reward, next_state, 0))

后面进行了一下验证：
使用的算法为nature-dqn，先看一下其余参数设置：
epsilon 经过10万帧后从1下降到0.02
batch_size = 32

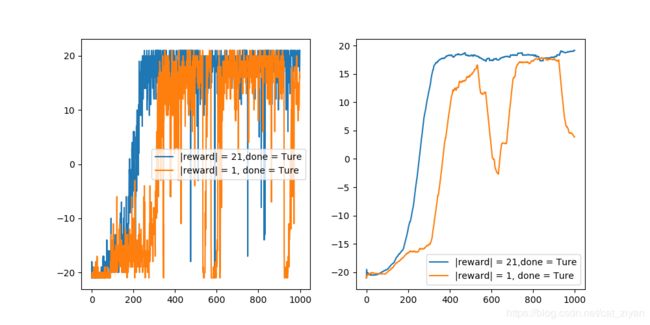
左图为每一回合的得分，右图为100个回合的平均值，可以看出，当 |reward| = 1时，收敛性特别差！
但这是否意味着以丢球作为结束判断不可行呢？我思考了一下会不会是学习率的原因。下图当|reward| = 1，done=True时，改变学习率后的对比图

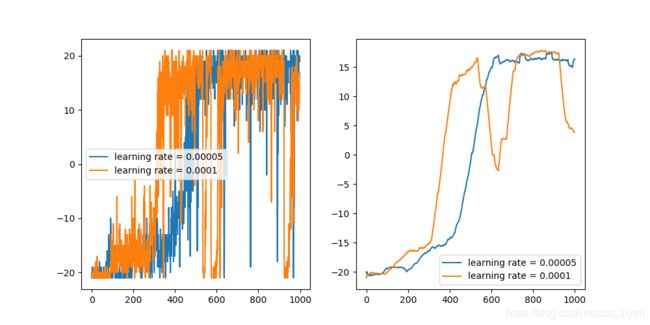
可以看出当学习率为0.00005时，虽然学习的比较慢，但是确实更稳定了，也就是说还是可以收敛的，除此之外，因为探索率$ϵ$为0.02，非常小，所有还有可能很多随机情况出现的时候，一些策略并没有学习到，所以导致会连续丢球。
下面我使用double-dqn结合dueling-dqn的算法，$ϵ=0.05,lr=0.0001$,|reward| = 1，done=True结果如下所示：

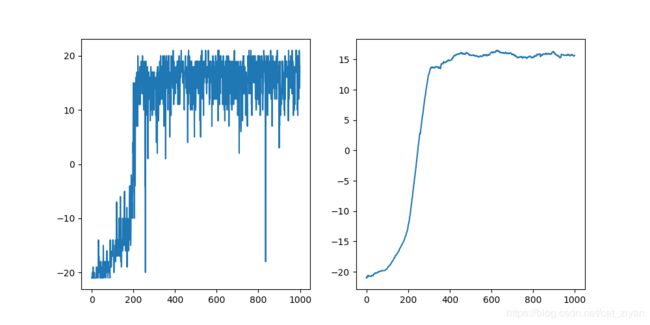
可以看出结果也可以收敛。所以改变结束判断依据时，需要相应的适当调整参数。