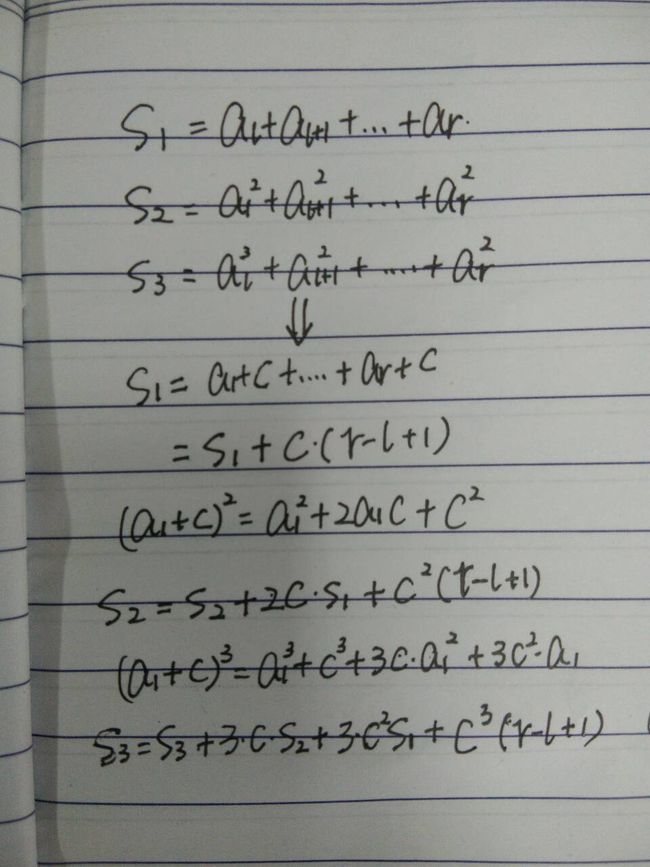HDU-4578 线段树 懒惰标记的下推顺序（好题）

链接  点击打开链接

Yuanfang is puzzled with the question below: 
There are n integers, a ₁, a ₂, …, a _n. The initial values of them are 0. There are four kinds of operations.
Operation 1: Add c to each number between a _x and a _y inclusive. In other words, do transformation a _k<---a _k+c, k = x,x+1,…,y.
Operation 2: Multiply c to each number between a _x and a _y inclusive. In other words, do transformation a _k<---a _k×c, k = x,x+1,…,y.
Operation 3: Change the numbers between a _x and a _y to c, inclusive. In other words, do transformation a _k<---c, k = x,x+1,…,y.
Operation 4: Get the sum of p power among the numbers between a _x and a _y inclusive. In other words, get the result of a _x ^p+a _x+1 ^p+…+a _y  ^p.
Yuanfang has no idea of how to do it. So he wants to ask you to help him. 

 

Input

There are no more than 10 test cases.
For each case, the first line contains two numbers n and m, meaning that there are n integers and m operations. 1 <= n, m <= 100,000.
Each the following m lines contains an operation. Operation 1 to 3 is in this format: "1 x y c" or "2 x y c" or "3 x y c". Operation 4 is in this format: "4 x y p". (1 <= x <= y <= n, 1 <= c <= 10,000, 1 <= p <= 3)
The input ends with 0 0.

 

Output

For each operation 4, output a single integer in one line representing the result. The answer may be quite large. You just need to calculate the remainder of the answer when divided by 10007.

 

Sample Input

5 53 3 5 71 2 4 44 1 5 22 2 5 84 3 5 30 0

 

Sample Output

3077489

题意应该简单，多种区间修改，区间幂次和的查询。

手动模拟一下区间加C的操作，这种操作对区间幂次和的影响是最大的也是相对较难的，但也是简单的。

如下图所示：很简单吧。。。

因此我们的更新顺序为S3-->S2-->S1。因为由上图可知它们是互相影响的。

然后其他两种操作就很简单了。

用mul【】表示乘的标记，add【】表示加的标记，che【】表示变成的操作。

然后重要的就是3个标记的下推顺序。其实是跟四则运算的顺序是一样的。还有che【】操作的级别应该是最高的

che【】-->mul【】-->add【】。

但是我们要在之前的更新操作一下，使得下推顺序满足这个顺序，其实也不难，真的。

首先要知道懒惰标记的意思是当前节点已经更新了，但是子节点没有更新。

例如：

当前是 变成 C 操作，就要对che【】更新为C，mul【】变成1（乘一相当于没操作，你总不能标记0吧），add【】变成 0 ，子节点也是同样的变化。

当前是 乘以 C 操作，mul【】=mul【】*C，那么对于add【】呢，本来是每个子节点都要加add【】，但是现在有要乘以C那么就是 add【】=add【】*C，对于che【】并没有影响，因为在下推的时候che【】是优先的。子节点也是同样的变化。

当前是 加上 C 操作 那是最简单的了，直接add【】=add【】+C，子节点也是同样的变化。

敲好之后，Wa了n发，开始瞎改精度的问题（其实是不可能的。。。），，结果是在查询的时候没有下推标记。

AC代码：

#include
using namespace std;
typedef long long ll;
const int maxn=100010;
const ll mod=10007;
int n,m;
int op,x,y;
ll v;
ll sum[maxn<<2][3],mul[maxn<<2],add[maxn<<2],che[maxn<<2];
void build(int root,int l,int r)
{
    sum[root][0]=sum[root][1]=sum[root][2]=0;
    mul[root]=1; add[root]=0; che[root]=0;
    if(l==r) return;
    int mid=l+r>>1;
    build(root<<1,l,mid);
    build(root<<1|1,mid+1,r);
}
void up(int root)
{
    for(int i=0;i<3;i++)
        sum[root][i]=(sum[root<<1][i]+sum[root<<1|1][i])%mod;
}
void up1(int root,ll c,int l,int r)
{
    int len=r-l+1;
    sum[root][2]=(sum[root][2]+c*c%mod*c%mod*len%mod+3*c*sum[root][1]%mod+3*c*c%mod*sum[root][0]%mod)%mod;
    sum[root][1]=(sum[root][1]+c*c%mod*len%mod+2*c*sum[root][0]%mod)%mod;
    sum[root][0]=(sum[root][0]+c*len)%mod;
}
void up2(int root,ll c)
{
    sum[root][2]=sum[root][2]*c%mod*c%mod*c%mod;
    sum[root][1]=sum[root][1]*c%mod*c%mod;
    sum[root][0]=sum[root][0]*c%mod;
}
void up3(int root,ll c,int l,int r)
{
    int len=r-l+1;
    sum[root][0]=c*len%mod;
    sum[root][1]=c*c%mod*len%mod;
    sum[root][2]=c*c%mod*c%mod*len%mod;
}
void down(int root,int l,int r)
{
    int lr=root<<1,rr=root<<1|1;
    int mid=l+r>>1;
    if(che[root])
    {
        che[lr]=che[rr]=che[root];
        mul[lr]=mul[rr]=1;
        add[lr]=add[rr]=0;
        ll c=che[root];
        up3(lr,c,l,mid);
        up3(rr,c,mid+1,r);
        che[root]=0;
    }
    if(mul[root]!=1)
    {
        mul[lr]=mul[lr]*mul[root]%mod;
        mul[rr]=mul[rr]*mul[root]%mod;
        if(add[lr]) add[lr]=add[lr]*mul[root]%mod;
        if(add[rr]) add[rr]=add[rr]*mul[root]%mod;
        up2(lr,mul[root]);
        up2(rr,mul[root]);
        mul[root]=1;
    }
    if(add[root])
    {
        add[lr]=(add[lr]+add[root])%mod;
        add[rr]=(add[rr]+add[root])%mod;
        up1(lr,add[root],l,mid);
        up1(rr,add[root],mid+1,r);
        add[root]=0;
    }
}
void updata(int root,int nowa,int nowb,int l,int r,int p,int c)
{
    if(nowb