差分数组:数列游戏、Color the ball、分苹果
一、差分数组的定义及用途
1.定义:
对于已知有n个元素的离线数列d,我们可以建立记录它每项与前一项差值的差分数组f:显然,f[1]=d[1]-0=d[1];对于整数i∈[2,n],我们让f[i]=d[i]-d[i-1]。
2.简单性质:
(1)计算数列各项的值:观察d[2]=f[1]+f[2]=d[1]+d[2]-d[1]=d[2]可知,数列第i项的值是可以用差分数组的前i项的和计算的,即d[i]=f[i]的前缀和。
(2)计算数列每一项的前缀和:第i项的前缀和即为数列前i项的和,那么推导可知
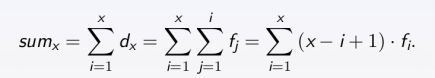
即可用差分数组求出数列前缀和;
3.用途:
(1)快速处理区间加减操作:
假如现在对数列中区间[L,R]上的数加上x,我们通过性质(1)知道,第一个受影响的差分数组中的元素为f[L],即令f[L]+=x,那么后面数列元素在计算过程中都会加上x;最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x,即可保证不会影响到R以后数列元素的计算。这样我们不必对区间内每一个数进行处理,只需处理两个差分后的数即可;
(2)询问区间和问题:
由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值;那么显然,区间[L,R]的和即为ans=sum[R]-sum[L-1];
二、相关题目
分苹果
问题描述
小朋友排成一排,老师给他们分苹果。
小朋友从左到右标号1..N。有M个老师,每次第i个老师会给第Li个到第Ri个,一共Ri-Li+1个小朋友每人发Ci个苹果。
最后老师想知道每个小朋友有多少苹果。
输入格式
第一行两个整数N、M,表示小朋友个数和老师个数。
接下来M行,每行三个整数Li、Ri、Ci,意义如题目表述。
输出格式
一行N个数,第i个数表示第i个小朋友手上的水果。
样例输入
5 3
1 2 1
2 3 2
2 5 3
样例输出
1 6 5 3 3
数据规模和约定
40%的数据,N、M≤1 000。
100%的数据,N、M≤100 000,1≤Li≤Ri≤N,0≤Ci≤100。
代码
package 摘东西;
import java.util.Scanner;
public class 分苹果1 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int[] d=new int[n+5];//d[i]表示第i个小朋友比第i-1个小朋友多的苹果
int lb,ub,c;
while(m--!=0){
lb=sc.nextInt();
ub=sc.nextInt();
c=sc.nextInt();
d[lb]+=c;//每一次发苹果第lb个小朋友比第lb-1个小朋友多c个
d[ub+1]-=c;//第r+1个小朋友比第r个小朋友少c个
}
for(int i=1;i<=n;i++){
d[i]+=d[i-1];//根据差分数组的性质进行求和
System.out.print(d[i]+" ");
}
}
}
[HDU1556]Color the ball
Description
-N个气球排成一排,从左到右依次编号为1,2,3…N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了,你能帮他算出每个气球被涂过几次颜色吗?
-Input:每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行,每行包括2个整数a b(1 <= a <= b <= N)。当N = 0,输入结束。
-Output:每个测试实例输出一行,包括N个整数,第I个数代表第I个气球总共被涂色的次数。
package 差分数组;
import java.util.Scanner;
public class ColorTheBall {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[] d=new int[n+5];
int lb,ub;
int temp=n;
while(temp--!=0){
lb=sc.nextInt();
ub=sc.nextInt();
d[lb]+=1;
d[ub+1]-=1;
}
for(int i=1;i<=n;i++){
d[i]+=d[i-1];
System.out.print(d[i]+" ");
}
}
}

3.用途:
(1)快速处理区间加减操作:
假如现在对数列中区间**[L,R]上的数加上x**,我们通过性质(1)知道,第一个受影响的差分数组中的元素为f[L],即令f[L]+=x,那么后面数列元素在计算过程中都会加上x;最后一个受影响的差分数组中的元素为f[R],所以令f[R+1]-=x,即可保证不会影响到R以后数列元素的计算。这样我们不必对区间内每一个数进行处理,只需处理两个差分后的数即可;
(2)询问区间和问题:
由性质(2)我们可以计算出数列各项的前缀和数组sum各项的值;那么显然,区间[L,R]的和即为ans=sum[R]-sum[L-1];
[NKOJ3754]数列游戏
Description
-给定一个长度为N的序列,首先进行A次操作,每次操作在Li和Ri这个区间加上一个数Ci。
然后有B次询问,每次询问Li到Ri的区间和。
初始序列都为0。
-输入格式:
第一行三个整数N A B。(1<=N<=1000000,1<=A<=N,A<=B<=N)
接下来A行,每行三个数Li Ri Ci。(1<=Li<=N,Li<=Ri<=N,|Ci|<=100000000000000)。
接下来B行,每行两个数 Li Ri。范围同上。
-输出格式:
对于每次询问,输出一行一个整数。
因为最后的结果可能很大,请对结果mod 1000000007。
package 差分数组;
import java.util.Scanner;
public class 数列游戏 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int a=sc.nextInt();
int b=sc.nextInt();
long mod=1000000007;
int[] d=new int[n+5];
int[] sum=new int[n+5];
int lb,ub,c;
while(a--!=0){
lb=sc.nextInt();
ub=sc.nextInt();
c=sc.nextInt();
d[lb]+=c;
d[lb]%=mod;
d[ub+1]-=c;
d[ub+1]%=mod;
}
for(int i=1;i<=n;i++){
d[i]+=d[i-1];
d[i]%=mod;
}
for(int i=1;i<=n;i++){
sum[i]=(sum[i-1]+d[i]);
sum[i]%=mod;
}
for(int i=1;i<=b;i++){
int l,r;
l=sc.nextInt();
r=sc.nextInt();
System.out.println(sum[r]-sum[l]);
}
}
}