KMP算法详解及next数组代码解释

KMP算法详解及next数组代码解释

KMP算法理解起来并不算太过于困难，从图像实例可以很直观得明晰算法原理，难点在于理解KMP算法中生成next数组的代码：

void next(char *s,int *next)
{
	int k = -1;
	int j =  0;
	next[0] = -1;
	while( j < strlen(s))
	{
		if(k == -1 || s[k] == s[j])
		{
			k++;
			j++;
			next[j] = k;
		}
		else
			j = next[j];
	}
}

我们先从概念上了解KMP算法的原理，首先从BF算法开始。

一、从BF算法开始

所谓BF算法（Brute Force)，也就是普通的模式匹配算法。假设我们要从主串 S = “ABCABD”中匹配模式串 P = “ABD”：
1.主串S从0位开始，前两位都与模式串P相互匹配，S[0] = P[0],S[1] = P[1],直到S[2] != P[2]。

2.主串S向后前进一位，P串归0，重新匹配，S[1] ！= P[0]。

3.主串S向后前进一位，P串归0，重新匹配，S[2] ！= P[0]。

4.主串S向后前进一位，P串归0，重新匹配，全部匹配成功。
算法代码如下：

//返回模式串在主串中的位置
int Index(char *s,char *p)
{
	int i = 0;
	int j = 0;
	while(i < strlen(s) && j < strlen(p))
	{
		if(s[i] == p[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i-j+1;
			j = 0;
		}
	}
	if( j == strlen(p))
		return i - strlen(p);
	else
		return -1;
}

BF算法的概念就是遍历主串中的字符，依次与模式串比较，如果出现不同，就将主串向后一位，再与模式串从头比较。我们能发现，这样效率很低，比如算法中的2步是没有必要的，直接进行第3步即可。原因很简单，我们已经知道模式串中‘A’,‘B’,‘C’,各不相同，即P[0] != P[1] != P[2],又从第一步中得知主串S[1] == P[1]，因此P[0] ！= S[1]。
KMP算法就可以避免出现这样不必要的步骤。

二、KMP算法

以下内容图片摘自阮一峰字符串匹配的KMP算法
同样，我们从一个例子开始，看看KMP算法不同之处在哪里：
1.

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。
2.

因为B与A不匹配，搜索词再往后移。
3.

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。
4.

接着比较字符串和搜索词的下一个字符，还是相同。
5.

直到字符串有一个字符，与搜索词对应的字符不相同为止。
6.

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。(也就是之前介绍的BF算法的思路）
7.

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。
8.

怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。
9.

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

移动位数 = 已匹配的字符数 - 对应的部分匹配值

因为 6 - 2 等于4，所以将搜索词向后移动4位。
10.

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（“AB”），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。
11.

因为空格与A不匹配，继续后移一位。
12.

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。
13.

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。
14.

下面介绍《部分匹配表》是如何产生的。

首先，要了解两个概念：“前缀"和"后缀”。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。
15.

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

－　"A"的前缀和后缀都为空集，共有元素的长度为0；

－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

－　“ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A”，长度为1；

－　“ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB”，长度为2；

－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，“ABCDAB"之中有两个"AB”，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

那么下面给出KMP算法代码：

void get_next(char *s,int *next)
{
	int k = -1;
	int j =  0;
	next[0] = -1;
	while( j < strlen(s))
	{
		if(k == -1 || s[k] == s[j])
		{
			k++;
			j++;
			next[j] = k;
		}
		else
			k = next[k];
	}
}
int KMP_Index(char *s,char *p)
{
	int i = 0;
	int j = -1;
	int next[255];
	get_next(p,next);
	int s_length = strlen(s);
	int p_length = strlen(p);
	while(i < s_length && j < p_length)
	{
		if(j == -1 || s[i] == p[j])
		{
			i++;
			j++;
		}
		else
			j = next[j];
	}
	if( j == strlen(p))
		return i - strlen(p);
	else
		return -1;
}

三、代码详解

此部分内容参考自唐小喵KMP算法的Next数组详解

1. get_next函数

先附代码：

void get_next(char *p,int *next)
{
	int k = -1;
	int j =  0;
	next[0] = -1;
	while( j < strlen(p))
	{
		if(k == -1 || p[k] == p[j])
		{
			k++;
			j++;
			next[j] = k;
		}
		else
			k = next[k];
	}
}

这也是关于KMP算法疑问最多的地方，next数组是如何得到的？关键在于要牢牢记住next数组中值的含义到底是什么，记住这一点才能更好得理解next数组。根据前文，next数组中每一项的值都是该位置字符之前子串的相等最长前后缀长度。举个例子：P = “ABABC"，‘C’字符对应next[4]，‘C’字符之前的子串的前缀为’A’,‘AB’,‘ABA’后缀为’B’,‘AB’,'BAB’那么相等最长前后缀就是’AB‘。所以next[4] == 2。

现在我们来看代码。k、j分别代表指向前缀数值和后缀数值，next[0]即对应了P串0位置之前子串的相等最长前后缀长度，0已经是第一个字符了，之前不存在子串，因此，将next[0]设置为-1。循环中每一轮求得的是next[j+1]。
（1）初始状态：初始状态进入循环，此时j = 0,因此求的是j+1 = 1位置的next，进入if条件判断得next[1] = 0，因为next[1]之前的子串只是单个字符，无前后缀。
（2）一般状态：假设j位和j之前的next已经填完，此时进入循环，如何求next[j+1]。如图：

分析图得：
a.由"next[j] == k;"这个条件，我们可以得到A1子串 == A2子串（根据next数组的定义，前后缀那个）。

b.由"next[k] == 绿色色块所在的索引;"这个条件，我们可以得到B1子串 == B2子串。

c.由"next[绿色色块所在的索引] == 黄色色块所在的索引;"这个条件，我们可以得到C1子串 == C2子串。

d.由1和2(A1 == A2，B1 == B2)可以得到B1 == B2 == B3。

e.由2和3(B1 == B2， C1 == C2)可以得到C1 == C2 == C3。

f.B2 == B3可以得到C3 == C4 == C1 == C2
现在要求next[j+1]：
如果k == j，那么如图所示，j+1之前的相等最长前后缀长度自然是A1+k == A2+j也就是红色这一部分，即next[j+1] = k+1;
如果k != j,相等最长前后缀长度就有可能是B1+next[k] == B3+j也就是绿色部分
依然不相等，则继续向前寻找最长的相等前后缀，即黄色部分，以此类推，直到不存在相等前后缀，那么next[j+1] = 0；
上述分析部分就是else语句的原理，通过不断向前寻找最长相等前缀，直到j == 0，回到初始。
我们拿一个实例来看：
假设P = “ABABEFABAB k … ABABEFABAB j j+1…”
由上分析:
A1 = A2 = “ABABEFABAB”
B1 = B2 = B3 = “ABAB”
C1 = C2 = C3 = C4 = “AB”
1、k == j next[j+1] = 11 最长相同前后缀：“ABABEFABABk（j）”
2、k != j 如k == X，j == A 通过回溯k,最终得到next[j+1] = 3 前后缀：“ABA” ，即C1k == C4j.

2、 KMP_Index函数

int KMP_Index(char *s,char *p)
{
	int i = 0;
	int j = -1;
	int next[255];
	get_next(p,next);
	int s_length = strlen(s);
	int p_length = strlen(p);
	while(i < s_length && j < p_length)
	{
		if(j == -1 || s[i] == p[j])
		{
			i++;
			j++;
		}
		else
			j = next[j];
	}
	if( j == strlen(p))
		return i - strlen(p);
	else
		return -1;
}

这一部分就很简单了，先求得P串的next数组，然后和BF算法类似，如果模式串和主串不相等了，就返回到next中储存的位置。

四、代码优化

我们已经了解了KMP算法，但是这其中有一些小问题。
例如，假设P = “AAAX”；next数组值是-1，0，1，2，原串S = “AAAAAB”，使用KMP算法进行对比时，发现：





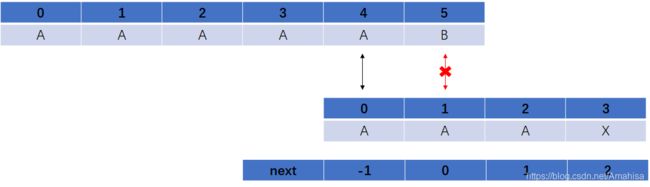
可以看出中间的步骤也是不必要的，因为P中1、2位置的字符与0是一样的，所以如果用next[0]来代替后续next[j]，即可以对KMP算法进行优化了。代码如下：

void get_next(char *p,int *next)
{
	int k = -1;
	int j =  0;
	next[0] = -1;
	while( j < strlen(p))
	{
		if(k == -1 || p[k] == p[j])
		{
			k++;
			j++;
			if(p[k] != p[j])
				next[j] = k;
			else
				next[j] = next[k];
		}
		else
			k = next[k];
	}
}

五、总结

KMP算法的重点其实就是如何获得next数组的问题，而明白这个问题最重要的，就是理解next中储存的值的意义到底是什么。网上就KMP算法已经有相当多的内容可以参考和借鉴，我自己在写这篇博文时也多有参考别人的文章，所以如果我所写的内容能对你有些许帮助，那就太好了，内容如果有错误和疏漏，也欢迎大家指出。

参考资料

阮一峰 字符串匹配的KMP算法
唐小喵 KMP算法的next数组详解
严蔚敏 数据结构（C语言版）