【POJ 1987】树的点分治 Distance Statistics

Frustrated at the number of distance queries required to find a reasonable route for his cow marathon, FJ decides to ask queries from which he can learn more information. Specifically, he supplies an integer K (1 <= K <= 1,000,000,000) and wants to know how many pairs of farms lie at a distance at most K from each other (distance is measured in terms of the length of road required to travel from one farm to another). Please only count pairs of distinct farms (i.e. do not count pairs such as (farm #5, farm #5) in your answer). 

Input

* Lines 1 ..M+1: Same input format as in "Navigation Nightmare" 

* Line M+2: A single integer, K. 

Output

* Line 1: The number of pairs of farms that are at a distance of at most K from each-other. 

Sample Input

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
10

Sample Output

5

Hint

There are 5 roads with length smaller or equal than 10, namely 1-4 (3), 4-7 (2), 1-7 (5), 3-5 (7) and 3-6 (9). 

    最近复习了分治，还学了一些以前没有学过的分治（像什么三分啊、树上的分治啊之类的），这道题就是一道典型的树分治（然而打脸的是做了2小时，TLE了10+次）。

    题意大概是说给出一个带权图（显然是棵树），求图中（树上）距离不超过k的节点对数，我们可以使用树分治来做。

    所谓树分治，就是在树上做分治，将问题转化为规模更小的几个问题，在子树中分别求解。为了让分解的规模更平均，我们必须找到树上的重心，因为这样才可以将子问题分得更小，方便我们求解（不TLE）。重心，就是将其拆掉后原图分成的几颗树中节点最多的树的节点数量在所有节点中最小的节点（好像有些绕）。

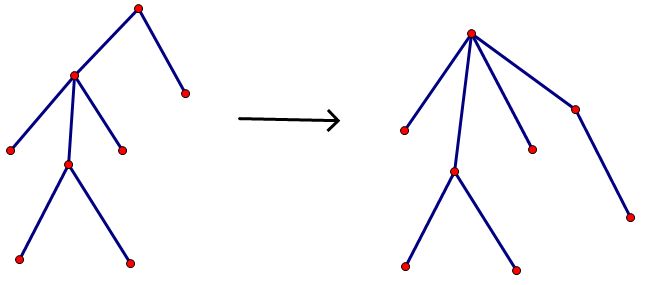
    画图说明吧！如下图，重心即为右图的根节点，因为当他被拆掉时，分出来的树最多有3个节点，而其他的都不能做到比他更少

    我们可以用一遍dfs求出一个重心，然后进行统计。

    此时，设我们已经找到重心r，那么距离小于k的节点对共有两种可能：1.他们之间跨越了r，2.他们之间并没有跨越r，第2种可以递归求解，所以我们只看第一种。将每个点到根节点的距离求出来，进行排序，然后线性寻找满足条件的，最后只要再减去来自同一子树的情况即可（因为他们肯定会在子树中再被计算）。

    当然，这样做的效率并不很高，要注意各种各样的细节处理以防像我一样TLE很多次……

    好了，不说了，放代码：（别在意我的注释）

#include
#include
#include
#include
#include
#include
using namespace std;
#define N 40005
#define M 80005
int n;
int m;//花瓶×1
int fir[N],t[M],nex[M],cnt,son[N],most[N]={0x3f3f3f3f},root,tot;
int k,l[M],dis[N],dis2[N];
bool vis[N];
void add(int a,int b,int c)
{
	cnt++;
	t[cnt]=b;
	nex[cnt]=fir[a];
	l[cnt]=c;
	fir[a]=cnt;
}
void dfs(int r,int f)//重心...
{
	son[r]=1;most[r]=0;
	for(int i=fir[r];i;i=nex[i])
	{
		int v=t[i];
		if(v!=f&&!vis[v])
		{
			dfs(v,r);
			most[r]=max(most[r],son[v]);
			son[r]+=son[v];
		}
	}
	most[r]=max(n-son[r],most[r]);
	if(most[r]zb&&dis2[zb]+dis2[yb]>k)
			yb--;
		sum+=yb-zb;
		zb++;
	}
	return sum;
}
int ans(int r)
{
	vis[r]=1;
	dis[r]=0;int sum=num(r);
	for(int i=fir[r];i;i=nex[i])
	{
		int v=t[i];
		if(!vis[v])
		{
			sum-=num(v);
			n=son[v];
			dfs(v,root=0);
			sum+=ans(root);
		}
	}
	/*for(int i=fir[r];i;i=nex[i])
	{
		int v=t[i];
		if(!vis[v])
		{
			n=son[v];
			dfs(v,root=0);
			sum+=ans(root);
		}
	}*/
	return sum;
}
int main()
{
	//freopen("1.txt","r",stdin);
	//int start=clock();
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int a,b;
		int c;
		char S[5];//花瓶×2
		scanf("%d%d%d%s",&a,&b,&c,S);
		add(a,b,c);
		add(b,a,c);
	}
	scanf("%d",&k);
	dfs(1,0);
	printf("%d",ans(root));
	//int End=clock();
	//printf("\n%d",End-start);
}