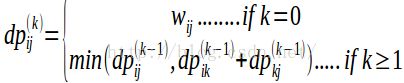所有节点对的最短路径问题
前面在《单源最短路径》中我们接触了最短路径问题,并介绍了求解最短路径问题的算法,比如Bellman-Ford算法,Dijkstra算法。不过,那里我们计算的是从一个固定的源节点到所有其他点的最短路径。假如我们要想求任意节点对之间的最短路径呢?一个方法是以所有节点作为源节点调用上述比如Dijkstra算法,如果使用二叉堆实现最小优先队列时间复杂度为O(VElgV),如果使用斐波那契堆来实现最小优先队列时间复杂度为O(V^2lgV+VE)。如果图中包含权值为负的边,将不能使用Dijkstra算法,而只能用Bellman-Ford算法,时间复杂度为O(V^2E),稠密图的情况下,时间复杂度为O(V^4)。本文将介绍更加高效的算法。
1.Floyd-Warshall算法
首先要求图可以有负权值的边,但是不能有负权值的环。该算法采用的是动态规划来解决问题的。关于动态规划的更过内容可以参考前面的文章《动态规划专题(I)》《动态规划专题(II)》《动态规划专题(III)》,其中介绍了动态规划的知识以及大量用动态规划来解决的问题。
最短路径结构
Flyod-Worshall算法考虑的是一条最短路径上的中间节点。假定图G的所有节点为V = {1,2,...,n},Floyd-Warshall算法利用了路径p和从i到j之间中间节点取自集合{1,,2,...,k-1}的最短路径之间的关系(其中k是小于n的某个整数)。该关系依赖于节点k是否是路径p上的一个中间节点。
1.如果k不是路径p上的中间节点,则路径p上的所有中间节点都属于集合{1,,2,...,k-1}。因此,从节点i到节点j的中间取自集合{1,2,...,k-1}的一条最短路径也是从节点i到j的中间节点取自集合{1,2,...,k}的一条最短路径。
2.如果节点k是路径p上的中间节点,则将路径p分解为i--p1->k--p2->j。那么p1是从节点i到k的中间节点全部取自集合{1,2,...,k-1}的一条最短路径。类似的,p2是从节点k到j的中间节点全部取自集合{1,2,...,k-1}的一条最短路径。
这里的思想比起上面提到的之前文章中介绍的动态规划问题要难,没那么直观,作者的想法是非常巧妙的,我们应该加以总结学习。另外多说一句,虽然Floyd-Warshall算法比较难想到,但是它的一种特殊情况,就是《动态规划专题(III)》中的Minimum Path Sum问题。大家是否已经想到了,这个问题就是图中每个节点最多只能连接到其他两个节点的情况。
现在,我们来求递归解。
设dp_{ij}^{k}(其中i,j是下标,k是上标)表示从节点i到节点j的所有中间节点全部取自集合{1,2,...,k}的一条最短路径的权重。递推公式如下:
对于任意的i,j in V, dp_{ij}^{n} = delta(i,j)。
伪代码:下面的算法返回最短路径权重矩阵D^{(n)}(n为上标)。
FLOYD-WARSHALL (W)
1. n = W.rows
2. D^{(0)} = W
3. for k = 1 to n
4. let D^{(k)} = dp_{ij}^{(k)} be a new nxn matrix
5. for i = 1 to n
6. for j = 1 to n
7. dp_{ij}^{k} = min(dp_{ij}^{(k-1)},dp_{ik}^{(k-1)}+dp_{kj}^{(k-1)})
8. return D^{(n)}
时间复杂度theta(n^3)。
Java代码较长,单独放到《多源最短路径--Floyd-Warshall算法》中。
2. 有向图的传递闭包
定义图G的传递闭包为图G* = (V,E*),其中E* = {(i,j):如果图G包含一条从节点i到节点j的路径}.
我们定义:如果图G中存在一条从节点i到节点j的所有中间节点都取自集合{1,2,...,k}的路径,则t_{ij}^{(k)}为1;否则,t_{ij}^{(k)}为0。
递推公式与Floyd-Warshall算法形式是相同的,只不过把min和+分别替换为逻辑或操作与逻辑与操作。
伪代码实际Java代码均参照Floyd-Warshall算法即可。
3.用于稀疏图的Johnson算法
前面我们知道了Floyd-Warshall算法的复杂度为theta(n^3),这里的n就是节点数,如果我们对每对节点调用Dijkstra算法,如果使用二叉堆实现最小优先队列,那么时间复杂度为O(V^2lgV+VElgV),如果使用斐波那契堆实现最小优先队列,时间复杂度为O(V^2lgV+VE),可以看到,在图为稀疏图的情况下,这里的效率要比Floyd-Warshall算法高。
在《单源最短路径》中我们知道了Dijkstra算法要求边的权值不能为负,Johnson算法采用重新赋予权值的技术来规避这个约束。新赋予的权重必须满足两个性质:
1.对于所有节点对u,v in V,一条路径p是在使用权重函数w时从节点u到v的最短路径,当且仅当p是在使用权重函数w'时从u到v的一条最短路径
2. 对于所有的边(u,v),新权重w'(u,v)为非负值
关于第一个性质有下面的引理
引理1(重新赋予权重不会改变最短路径):给定带权重的有向图G=(V,E),其权重函数为w: E->R,设h: V-->R为任意函数,该函数将节点映射到实数上。对于每条边(u,v) in E,定义
w'(u,v) = w(u,v) + h(u) - h(v)
设p =
关于第二个性质,我们可以根据三角不等式来设计,对于任意节点v in V',h(v) = delta(s,v)。那么h(v) <= h(u)+w(u,v),因此有w'(u,v) = w(u,v) + h(u) - h(v) >= 0。
伪代码:
JOHNSON(G,w)
1. compute G',where G'.V = G.V U {s}
G'.E = G.E U {(s,v):v in G.V}, and
w(s,v) = 0 for all v in G.V
2. if BELLMAN-FORD(G',w,s) == FALSE
3. print .....
4. else for each vertex in G'.V
5. set h(v) to the value of delta(s,v) computed by the Bellman-Ford algorithm
6. for each edge edge(u,v) in G'.E
7. w'(u,v) = w(u,v) + h(u) - h(v)
8. let D = (d_{uv}) be a new nxn matrix
9. for each vertex u in G.V
10. run DIJSKRA(G,w',u) to compute delta'(u,v) for all v in G.v
11. for each vertex v in G.V
12. d_{uv} = delta'(u,v) + h(v) - h(u)
13. return D
Java代码实现比较长,我将其单独放到《稀疏图Johnson算法》中。
4.小结
前面我们在《最小生成树》中介绍了最小生成树算法:Kruskal和Prim算法;在《单源最短路径》中介绍了求解单源路径的算法:比如Bellman-Ford算法、有向无环图的单源最短路径这种特殊情况下的算法、Dijkstra算法。本篇文章中,我们又介绍了多源路径算法:Floyd-Warshall算法、用于稀疏图的Johnson算法。最小生成树算法属于贪心算法,其中Prim算法与Dijkstra算法及其相似;单源路径算法基本上是对路径松弛性质的应用;多源最短路径问题则需要动态规划。