(二)sklearn降维——PCA和LDA

线性判别分析（LDA）尝试识别占类之间差异最大的属性。特别地，与PCA相比，LDA是使用已知类标签的监督方法。

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()

X = iris.data
y = iris.target
target_names = iris.target_names

X.shape,y.shape,target_names

((150, 4), (150,), array(['setosa', 'versicolor', 'virginica'], dtype='

Iris数据集代表3种鸢尾花（Setosa，Versicolour和Virginica），具有4种属性：萼片长度，萼片宽度，花瓣长度和花瓣宽度。

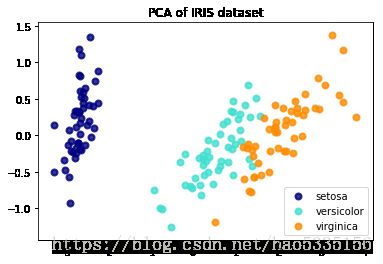
PCA把4种属性降维2种

pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)

X_r.shape

(150, 2)

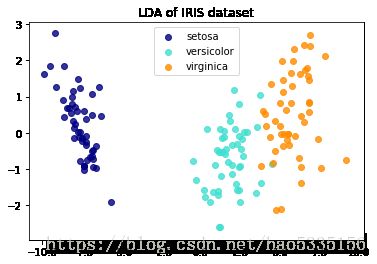
LDA把4种属性降维2种,LDA是使用已知类标签的监督方法

lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)

X_r2.shape

(150, 2)

# Percentage of variance explained for each components
#explained_variance_ 指每个选定的组件所解释的差异量，
#等于n_components的协方差矩阵的最大特征值(保留特征值最大的组分)
#PCA解释方差比,如果没有设置n_components，则会存储所有组件，解释方差之和为1.0。
print('explained variance ratio (first two components): %s'
      % str(pca.explained_variance_ratio_))

explained variance ratio (first two components): [0.92461621 0.05301557]

#绘图X_r[y == i, 0]代表第0个组分作为x轴，y == i代表标签为y的数据。
#一共3个类别，所有有3次不同颜色的绘图
plt.figure()
colors = ['navy', 'turquoise', 'darkorange']
lw = 2

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of IRIS dataset')

Text(0.5,1,'PCA of IRIS dataset')

plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.8, color=color,
                label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA of IRIS dataset')

plt.show()

分析:两种成分基本可以把3个类别区分，甚至一种成分(x轴的数据就可以，因为0.92461621代表大量的信息)