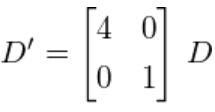摘抄 - 从几何角度看协方差矩阵
简介：
本文通过探索线性变换和变换后数据协方差的的关系，提供一个直观的、几何图示的协方差矩阵解释。大多数教材都是通过协方差矩阵的概念来解释数据的分布形状。相反的我们通过数据分布的形状来解释协方差矩阵。
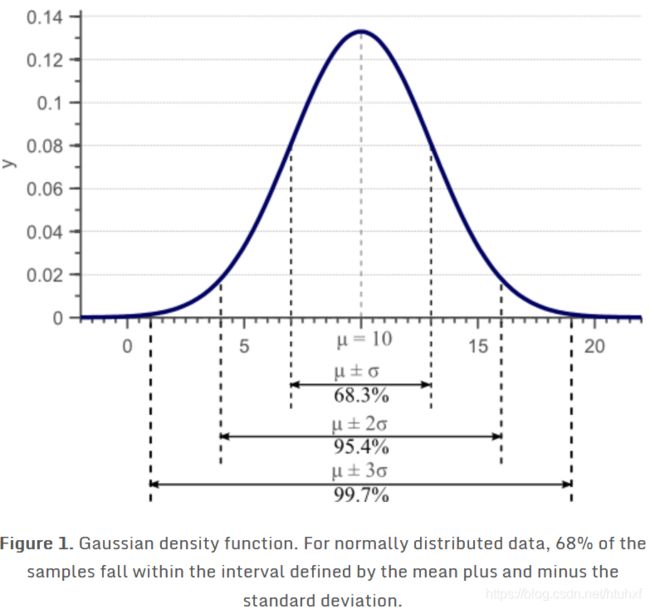
在先前的文章里我们探讨和方差的概念，并给出了预估方差的公式的推导和证明。这里Figure 1 展现了标准差——方差的根，量化了整个数据的分布：
下边这个公式可以获取样本方差的估计值：
σ 2 = 1 N − 1 ∑ i = 1 N ( x i − μ ) 2 = E [ ( x − E ( x ) ) ( x − E ( x ) ) ] = σ ( x , x ) \sigma^2=\frac{1}{N-1} \sum_{i=1}^N (x_i - \mu)^2 = E[(x-E(x))(x-E(x))] =\sigma(x, x) σ2=N−11i=1∑N(xi−μ)2=E[(x−E(x))(x−E(x))]=σ(x,x)
然而，方差只能解释数据在坐标轴方向的离散度。以Figure 2的数据为例
针对上图所示数据分布，我们可以计算出x坐标轴方向的方差 σ ( x , x ) \sigma(x,x) σ(x,x)和y坐标轴方向的方差 σ ( y , y ) \sigma(y,y) σ(y,y)。然而，水平分布和垂直分布不能解释明显的对角线线性相关。明显的Figure 2里边 y y y随 x x x的增大而增大，即 相 关 性 相关性 相关性——它可以通过拓展 方 差 / v a r i a n c e 方差/variance 方差/variance概念来量化描述：
σ ( x , y ) = E [ ( x − E ( x ) ) ( y − E ( y ) ) ] \sigma(x,y)=E[(x-E(x))(y-E(y))] σ(x,y)=E[(x−E(x))(y−E(y))]
我们称之为 协 方 差 / c o v a r i a n c e 协方差/covariance 协方差/covariance。对于二维数据数据，可以获取 σ ( x , x ) \sigma(x,x) σ(x,x)， σ ( y , y ) \sigma(y,y) σ(y,y)， σ ( x , y ) \sigma(x,y) σ(x,y)和 σ ( y , x ) \sigma(y,x) σ(y,x)，这四个值用一个矩阵来精炼的表示就是：
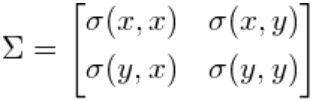
如果x和y正相关，则y和x也是正相关，即 σ ( x , y ) = σ ( y , x ) \sigma(x,y)=\sigma(y,x) σ(x,y)=σ(y,x)，因此，协方差矩阵总是对称的：它对角线上是Variances，其余的是covariances。二维正态分布的数据可用均值和 2 X 2 2X2 2X2协方差矩阵充分表示。类似的， 3 X 3 3X3 3X3协方差矩阵用来获取三维数据的分布状况， N X N NXN NXN协方差矩阵用来或许N维数据的分布状况。
Figure 3展示了数据分布如何定义协方差矩阵：
协方差矩阵的特征值分解
这里将讨论如何从线性变换的角度来理解协方差矩阵。在此之前，十分必要先从直观的角度看看特征值/eigenvalue和特征向量/eigenvector，是如何唯一定义协方差矩阵和数据分布形状。
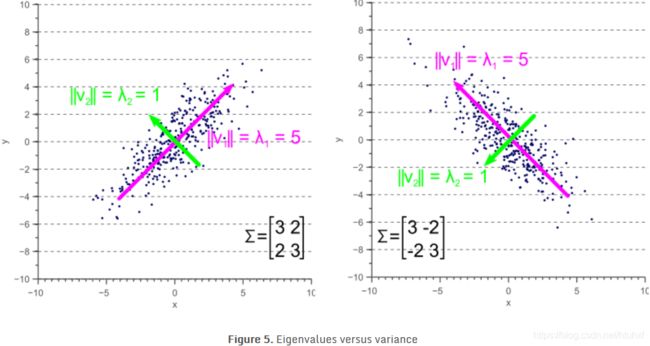
从Figure 3里我们看到，协方差矩阵定义了数据的 s p r e a d / [ v a r i a n c e ] spread/[variance] spread/[variance]和 o r i e n t a t i o n / [ c o v a r i a n c e ] orientation/[covariance] orientation/[covariance]，所以我们要从协方差矩阵里边找出最特殊也最具有代表性的direction vector和 scale value，也就是eigenvector和eigenvalue。
（感觉不容易理解的话，看下大神3Blue1Brown《线性代数的本质》之“特征向量和特征值”，小心！别沉迷其中不能自拔！）
我们知道：一个特征值/ λ \lambda λ、一个特征向量 / v ⃗ \vec{v} v以及一个矩阵/ Σ \Sigma Σ有如下关系：
Σ v ⃗ = λ v ⃗ = λ I v ⃗ \Sigma\vec{v}=\lambda\vec{v}=\lambda I \vec{v} Σv=λv=λIv
当协方差矩阵是对角矩阵的时候，此时 c o v a r i a n c e covariance covariance为0，此时意味着 v a r i a n c e variance variance一定等于特征值 λ \lambda λ，此时相当于把原来的基向量 i ⃗ / ( 1 , 0 ) T \vec{i}/(1,0)^T i/(1,0)T、 j ⃗ / ( 1 , 0 ) T \vec{j}/(1,0)^T j/(1,0)T进行了拉伸，结果见图 F i g u r e 4 Figure 4 Figure4：
当协方差矩阵不是对角矩阵的时候，相当于对基向量进行了拉伸的基础上又叠加了旋转：如Figure 5
协方差矩阵作为线性变换
我们先看个例子：Figure 3里任何一个分部都看作如下Figure 6经过某种线性变换得到
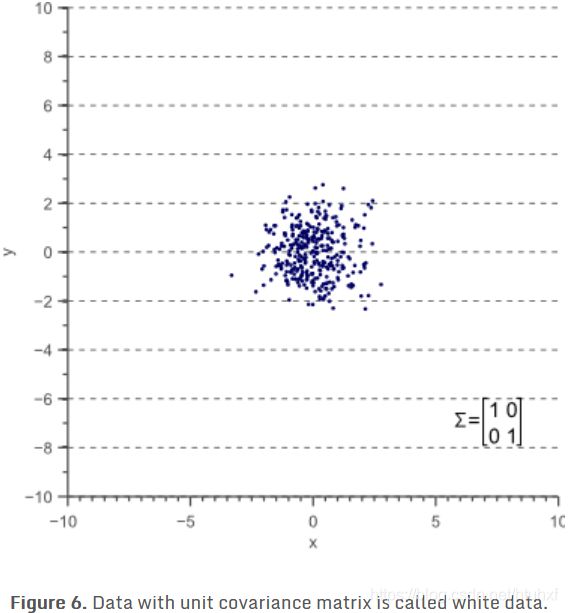我们用 D D D代表Figure 6的数据Data，这个线性变换矩阵用 T T T表示，则有：
D n e w = T D D_{new}=TD Dnew=TD
这个线性变换矩阵 T T T可以分解为旋转矩阵/Rotation Metrix和拉伸矩阵/Scaling Metrix，分别用 R R R和 S S S表示：
T = R S T=R S T=RS
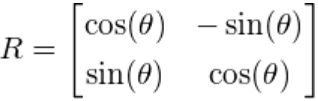
其中 θ \theta θ是旋转的角度
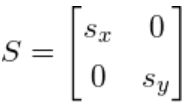
此处 s x s_x sx和 s y s_y sy分别是x轴方向和y轴方向的拉伸数值。
接下来我们讨论一下协方差矩阵 Σ \Sigma Σ和线性变换矩阵 T = R S T=RS T=RS的关系。
我们从一个“white data”着手因为数据来自于正态分布因此称之为white data，即它的误差是white/uncorrelated noise
上图的white data对应单位矩阵，即variance是1，covariance是0
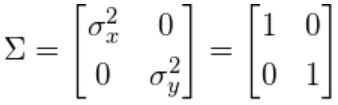现在让我们把x周的单位向量拉伸4倍：
D ′ D' D′分布图如下
它的协方差矩阵 Σ ′ \Sigma' Σ′
从先前的式子 Σ v ⃗ = λ v ⃗ \Sigma\vec{v}=\lambda\vec{v} Σv=λv可以引申到矩阵的表示：
Σ V = V L \Sigma V=VL ΣV=VL
此处， V V V是矩阵 Σ \Sigma Σ的特征向量组成的矩阵， L L L是其特征值组成的对角矩阵。
这就明显看出来，协方差矩阵是其特征向量和特征值的函数：
Σ = V L V − 1 \Sigma = V L V^{-1} Σ=VLV−1
上式就是协方差矩阵的特征值分解。此处的特征向量指向数据最大variance方向，特征值是这些variance在特征向量方向的拉伸数值，也正因此协方差矩阵又可以写作
Σ = R S S − 1 R − 1 = R S S R − 1 \Sigma = RS S^{-1}R^{-1}=RS SR^{-1} Σ=RSS−1R−1=RSSR−1
此处 R = V R=V R=V是旋转矩阵， S = L S=\sqrt{L} S=L是拉伸矩阵。
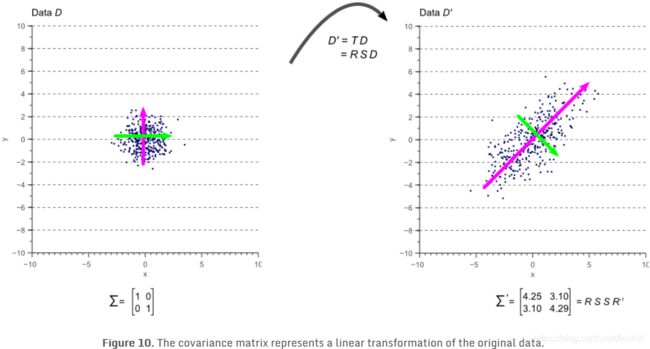
从上图可以看出来，最大的eigenvector指向最大的variance的方向，其余的eigenvector也一定是和最大的特征向量正交的（即向量乘积为0，相互垂直）。旋转矩阵是正交矩阵。
结论
在本文中我们可以看到任何一个数据的协方差矩阵都是和一个white & uncorrlelated data的线性变换直接相关的，该线性变换完全是由数据本身的特征向量和特征值决定；特征向量代表旋转矩阵，特征值是伸缩量。