R语言--粒子群优化算法PSO
粒子群优化算法(Particle Swarm Optimization,简称PSO)是通过模拟鸟群捕食行为设计的一种群智能算法。本文介绍算法原理,R代码实现以及R包实现。
粒子群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解。
PSO的优势在于简单容易实现并且没有许多参数的调节,广泛应用于函数优化、神经网络训练等领域。
算法原理
介绍
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟,粒子仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解,并将其记为当前个体极值,并将个体极值与整个粒子群里的其他粒子共享,找到最优的那个个体极值作为整个粒子群的当前全局最优解,粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程:
公式
PSO初始化为一群随机粒子,然后通过迭代找到最优解。在每一次的迭代中,粒子通过跟踪两个极值(pbest,gbest)来更新自己。在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置。
速度更新公式
V i = ω × V i + c 1 × r a n d ( ) × ( p b e s t i − X i ) + c 2 × r a n d ( ) × ( g b e s t − X i ) V_i=\omega\times V_i+c_1\times rand()\times (pbest_i-X_i)+c_2\times rand()\times (gbest-X_i) Vi=ω×Vi+c1×rand()×(pbesti−Xi)+c2×rand()×(gbest−Xi)
其中:
ω \omega ω为惯性因子,数值范围为0到1之间;
V i V_i Vi为第i个粒子的速度;
X i X_i Xi为第i个粒子的位置;
c 1 c_1 c1和 c 2 c_2 c2为学习因子,通常为2;
r a n d ( ) rand() rand()为0到1之间的随机数;
p b e s t i pbest_i pbesti为第i个粒子的历史最优位置;
g b e s t gbest gbest为粒子群的历史最优位置。
位置更新公式
X i = X i + V i X_i=X_i+V_i Xi=Xi+Vi
流程图
代码实现
用PSO算法解决一个实际的优化问题:
求解 z = x 2 + y 2 z=x^2+y^2 z=x2+y2在 x , y ∈ [ − 10 , 10 ] x,y\in[-10,10] x,y∈[−10,10]值域范围内的最小值。
- 函数定义
# 目标函数(x输入长度为2的向量)
fit <- function(x)sum(x^2)
# 值域
lower <- -10
upper <- 10
- 图像展示
library(plotly)
# 计算函数值矩阵
z <- apply(expand.grid(x=lower:upper,y=lower:upper),1,fit) %>% matrix(ncol = length(lower:upper))
# 3d展示
plot_ly(x=lower:upper,y=lower:upper,z=z) %>% add_surface()
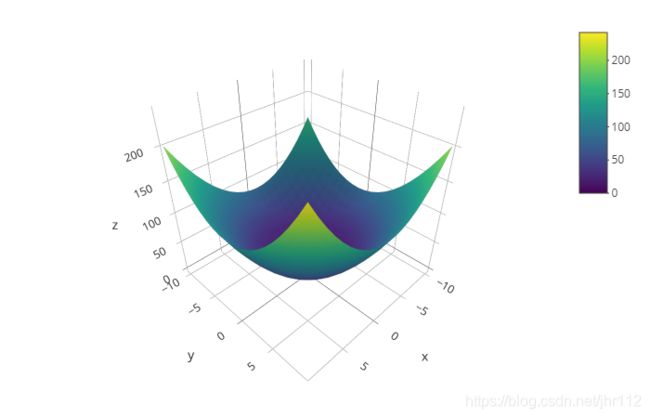
通过图像可知,该函数是一个“碗状”结构,在值域范围内有且只有一个最小值。
- 粒子群初始化
# 初始粒子数量
n <- 20
# 速度最大值
vmax <- 2
# 惯性因子
w <- 1
# 学习因子
c1 <- c2 <- 2
# 随机数
r1 <- runif(1)
r2 <- runif(1)
# 适应度变化初始值
gBestDelta <- NULL
# 最佳适应度变化阈值
alpha <- 0.0001
# 粒子群迭代次数
iters <- 1000
# 随机位置矩阵 X
X <- data.frame(x=runif(n,-10,10),y=runif(n,-10,10)) %>% as.matrix()
# 随机速度矩阵 V
V <- data.frame(x=runif(n,-vmax,vmax),y=runif(n,-vmax,vmax)) %>% as.matrix()
# pBest初始设置为X
pBest <- X
# gBest初始设置 gBest=min{pBesti}
gBest <- pBest[which.min(apply(pBest,1,fit)),]
- 粒子群迭代更新
# 结果向量
fitness <- c()
# 迭代
for(j in 1:iters){
# 粒子群更新
for(i in 1:n){
# 粒子速度更新
V[i,] <- w*V[i,]+c1*r1*(pBest[i,]-X[i,])+c2*r2*(gBest-X[i,])
# 粒子速度约束(超过最大速度则设置为最大速度)
V[i,V[i,]>vmax] <- vmax
# 粒子位置更新
X[i,] <- X[i,]+V[i,]
# 粒子pBest更新
if(fit(X[i,]) < fit(pBest[i,])) pBest[i,] <- X[i,]
# 粒子群gBest更新(全局解)
if(fit(pBest[i,]) < fit(gBest)){
gBestDelta <- abs(fit(gBest)-fit(pBest[i,])) # 粒子群适应度变化量
gBest <- pBest[i,]
}
}
# 存储每次迭代的结果
fitness[j] <- fit(gBest)
# 达到阈值条件则结束
if(!is.null(gBestDelta) & gBestDelta < alpha) break
}
- 输出结果
从计算结果可知,最优解x和y都非常小,约等于0。同时,从图中可以看出,PSO在迭代几十次后,拟合度下降的非常快,之后几乎不再变化,算法很快找到了全局最优解。
print(gBest)
## x y
## 0.010550688 0.009236431
plot(1:length(fitness),fitness,type="l",xlab="iters",ylab="fitness")
R包实现
R中有第三方包实现PSO算法–pso,同样,用该包实现上述优化问题求解。
- 安装包
install.packages("pso")
- psoptim函数
library(pso)
psoptim(par = rep(NA,2),fn = fit,lower = -10,upper = 10)
## $par
## [1] -4.761513e-48 4.881461e-48
##
## $value
## [1] 4.650066e-95
##
## $counts
## function iteration restarts
## 12000 1000 0
##
## $convergence
## [1] 2
##
## $message
## [1] "Maximal number of iterations reached"
从psoptm函数的计算结果可知,其中par表示计算参数结果,分别约等于0,value表示对于的优化函数值。更多的函数使用说明可以参考官方文档。



