R语言--邻近算法KNN
KNN(k邻近算法)是机器学习算法中常见的用于分类或回归的算法。它简单,训练数据快,对数据分布没有要求,使它成为机器学习中使用频率较高的算法,并且,在深度学习大行其道的今天,传统可解释的简单模型在工业大数据领域的应用更为广泛。本文介绍KNN算法的基本原理和用R代码实现。
算法介绍
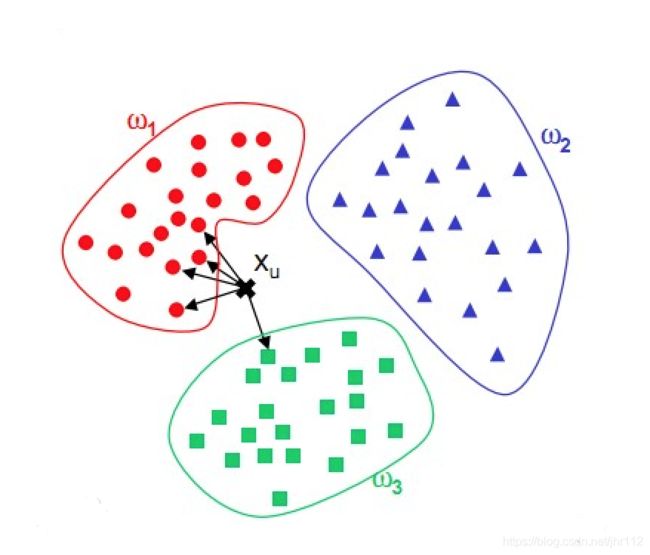
KNN的核心思想可以用平常的俗语表示"物以类聚,人以群分",就是相似的东西很有可能具有相似的属性。k邻近法假设给定一个训练数据集,其中的数据标签已给。对于新的样本,找到与其k个最近邻的训练数据,这k个训练数据的多数属于某个类,就把新样本归为这个类。
k近邻算法不具有显式的学习过程,不会从训练数据中学习到某个假设函数,用来预测,它实际上是利用训练数据对特征向量空间进行划分,并作为其学习出来的“模型”。
k值的选择,距离的度量是KNN算法的主要影响因素。
距离度量
距离度量是KNN中用来表示样本的距离大小的评价指标,选取不同的距离度量会产生精度不同的预测结果。
特征空间中两个实例点的距离是两个实例点相似程度的反映。k近邻模型的特征空间一般是n维实数向量空间 R n R^n Rn。使用的距离一般是欧式距离,欧式距离也是最常用的。也可以是其他距离,比如曼哈顿距离或者Minkowski距离等。
设特征空间 χ \chi χ是n维实数向量空间 R n R^n Rn, x i , x j ∈ χ x_i,x_j\in\chi xi,xj∈χ, x i = ( x i 1 , x i 2 , . . . , x i n ) T x_i=(x^1_i,x^2_i,...,x^n_i)^T xi=(xi1,xi2,...,xin)T, x j = ( x j 1 , x j 2 , . . . , x j n ) T x_j=(x^1_j,x^2_j,...,x^n_j)^T xj=(xj1,xj2,...,xjn)T, x i , x j x_i,x_j xi,xj的 L p L_p Lp距离定义为
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p ( p ≥ 1 ) L_p(x_i,x_j)=\left( \sum^n_{l=1}\left|x^{(l)}_i-x^{(l)}_j \right|^p \right)^\frac{1}{p} (p\ge1) Lp(xi,xj)=(l=1∑n∣∣∣xi(l)−xj(l)∣∣∣p)p1(p≥1)
当p=2时,为欧式距离(Euclidean distance),即
L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_2(x_i,x_j)=\left( \sum^n_{l=1}\left|x^{(l)}_i-x^{(l)}_j \right|^2 \right)^\frac{1}{2} L2(xi,xj)=(l=1∑n∣∣∣xi(l)−xj(l)∣∣∣2)21
当p=1时,为曼哈顿距离(Manhattan distance),即
L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_1(x_i,x_j)=\sum^n_{l=1}\left|x^{(l)}_i-x^{(l)}_j \right| L1(xi,xj)=l=1∑n∣∣∣xi(l)−xj(l)∣∣∣
在R语言中,内置的dist函数(stats包),可以很方便的计算各种距离。
# 样本矩阵(5个样本)
x <- matrix(1:100,nrow = 5)
# 距离计算(默认欧式距离)
dist(x)
## 1 2 3 4
## 2 4.472136
## 3 8.944272 4.472136
## 4 13.416408 8.944272 4.472136
## 5 17.888544 13.416408 8.944272 4.472136
# 曼哈顿距离
dist(x,method = "manhattan")
## 1 2 3 4
## 2 20
## 3 40 20
## 4 60 40 20
## 5 80 60 40 20
k值选取
相比于距离度量的选择,k值的选择对knn算法的性能影响更大。
如果选择较小的k值,就是意味着用较小的相邻训练数据进行预测,预测的结果会对近邻的训练数据非常敏感,当近邻的数据中存在噪声时,预测结果往往出现较大偏差,过小的k值会导致模型变得复杂,因此也更容易发生过拟合现象。
如果选择较大的k值,就相当于用较大邻域中的训练数据进行预测,与输入数据距离较远的训练数据也会对模型产生影响,往往使预测结果发生错误。过大的k值使得模型过于简单。
k值的选择,根据经验,一般在3~10之间。但在实际模型训练中,我们往往会自定义k值范围,采用网格搜索的方法去选择最佳k值。
特征的标准化
在应用knn算法进行建模前,必须要做的一件事就是特征标准化。因为knn依赖于距离的计算,现实数据中,各个特征的标度一般是不一样的,即数据范围有差异,假如某个特征的数值特别大,那么距离的度量就会强烈地被这个较大数值的特征所支配,其他特征起到的作用就很小了,模型也就失去了意义。
对特征标准化有多种方法,常见的有min-max标准化,z-score标准化等。
- min-max标准化
X为特征向量, X n e w X_{new} Xnew为min-max标准化后的特征向量。min-max标准化后的数值范围为[0,1]。
X n e w = X − m i n ( X ) m a x ( X ) − m i n ( X ) X_{new}=\frac{X-min(X)}{max(X)-min(X)} Xnew=max(X)−min(X)X−min(X)
- z-score标准化
μ \mu μ表示特征向量X的平均值, σ \sigma σ表示特征向量X的标准差。z-score标准化后的数值范围是无界的( − ∞ , ∞ -\infty,\infty −∞,∞)。
X n e w = X − μ σ X_{new}=\frac{X-\mu}{\sigma} Xnew=σX−μ
哑变量编码
在应用knn进行建模时,有一个前提就是训练数据的特征必须都是数值型的。假如此时训练数据中有名义特征(类别值),如果考虑将名义特征加入模型之中,那么就需要对名义特征进行哑变量编码,使名义特征变成数值特征。
假设有一个为gender(性别)的特征,取值范围是male或female,那么就可以产生一个新的数值特征male来代替gender,male的产生逻辑如下:
m a l e = { 1 如 果 x = m a l e 0 其 他 male=\left\{ \begin{aligned} 1 & & 如果x=male \\ 0 & & 其他 \\ \end{aligned} \right. male={10如果x=male其他
细节:
- 一般根据名义特征的类别数来定义产生新的哑变量个数,即名义特征类别数为n,则只需要产生n-1个哑变量。
- 名义变量类别数大于2,类别之间是平等地位,用0、1哑变量编码。
- 名义变量类别数大于2,类别之间有确定的递进关系,可以用1、2、3…编码,然后min-max标准化。
实战演练
数据准备
数据来源《机器学习与R语言》书中,具体来自UCI机器学习仓库。
地址:http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/
下载wbdc.data和wbdc.names这两个数据集,数据经过整理,成为面板数据。
由于外网访问慢,这里直接给出整理好的数据源:
百度网盘:https://pan.baidu.com/s/1NNoemlf7XCUHXgpy6gl85g 提取码:gi2d
数据预处理
读取数据:
data <- read.csv("wisc_bc_data.csv",stringsAsFactors = FALSE)
查看数据维度,568个样本,32个特征(包括响应特征)。
dim(data)
## [1] 568 32
查看数据结构,其中第一列为id列,无特征意义,需要删除。第二列diagnosis为响应变量,字符型,一般在R语言中分类任务都要求响应变量为因子类型,因此需要做数据类型转换。剩余的为预测变量,数值类型。
str(data)
## 'data.frame': 568 obs. of 32 variables:
## $ id : int 842517 84300903 84348301 84358402 843786 844359 84458202 844981 84501001 845636 ...
## $ diagnosis : chr "M" "M" "M" "M" ...
## $ radius_mean : num 20.6 19.7 11.4 20.3 12.4 ...
## $ texture_mean : num 17.8 21.2 20.4 14.3 15.7 ...
## $ perimeter_mean : num 132.9 130 77.6 135.1 82.6 ...
## $ area_mean : num 1326 1203 386 1297 477 ...
## $ smoothness_mean : num 0.0847 0.1096 0.1425 0.1003 0.1278 ...
## $ compactne_mean : num 0.0786 0.1599 0.2839 0.1328 0.17 ...
## $ concavity_mean : num 0.0869 0.1974 0.2414 0.198 0.1578 ...
## $ concave_points_mean : num 0.0702 0.1279 0.1052 0.1043 0.0809 ...
## $ symmetry_mean : num 0.181 0.207 0.26 0.181 0.209 ...
## $ fractal_dimension_mean : num 0.0567 0.06 0.0974 0.0588 0.0761 ...
## $ radius_se : num 0.543 0.746 0.496 0.757 0.335 ...
## $ texture_se : num 0.734 0.787 1.156 0.781 0.89 ...
## $ perimeter_se : num 3.4 4.58 3.44 5.44 2.22 ...
## $ area_se : num 74.1 94 27.2 94.4 27.2 ...
## $ smoothness_se : num 0.00522 0.00615 0.00911 0.01149 0.00751 ...
## $ compactne_se : num 0.0131 0.0401 0.0746 0.0246 0.0335 ...
## $ concavity_se : num 0.0186 0.0383 0.0566 0.0569 0.0367 ...
## $ concave_points_se : num 0.0134 0.0206 0.0187 0.0188 0.0114 ...
## $ symmetry_se : num 0.0139 0.0225 0.0596 0.0176 0.0216 ...
## $ fractal_dimension_se : num 0.00353 0.00457 0.00921 0.00511 0.00508 ...
## $ radius_worst : num 25 23.6 14.9 22.5 15.5 ...
## $ texture_worst : num 23.4 25.5 26.5 16.7 23.8 ...
## $ perimeter_worst : num 158.8 152.5 98.9 152.2 103.4 ...
## $ area_worst : num 1956 1709 568 1575 742 ...
## $ smoothness_worst : num 0.124 0.144 0.21 0.137 0.179 ...
## $ compactne_worst : num 0.187 0.424 0.866 0.205 0.525 ...
## $ concavity_worst : num 0.242 0.45 0.687 0.4 0.535 ...
## $ concave_points_worst : num 0.186 0.243 0.258 0.163 0.174 ...
## $ symmetry_worst : num 0.275 0.361 0.664 0.236 0.399 ...
## $ fractal_dimension_worst: num 0.089 0.0876 0.173 0.0768 0.1244 ...
查看数据缺失情况,发现无数据缺失,不需要做缺失值填补。
sum(is.na(data))
## [1] 0
数据预处理。
library(tidyverse)
data <- select(data,-1) %>%
mutate_at('diagnosis',as.factor)
数据分割
将原始数据分割成训练数据和测试数据,测试数据不参与训练建模,将根据模型在测试数据中的表现来选择最优模型参数。
一般做数据分割会留70%的训练数据和30%的测试数据,当然这个比例可以更改,但是一般是训练数据要大于测试数据,用来保证模型学习的充分性。
此外,在做分类任务时,有一个需要额外考虑的问题就是需要尽可能保证训练数据和测试数据中正负样本的比例相近。这里采用分层抽样来完成这个任务。
library(sampling)
set.seed(123)
# 每层抽取70%的数据
train_id <- strata(data,'diagnosis',size = rev(round(table(data$diagnosis)*0.7)))$ID_unit
# 训练数据
train_data <- data[train_id,]
# 测试数据
test_data <- data[-train_id,]
可以检查一下数据分割后是否保证了训练数据和测试数据中正负样本比例相同。
# 查看训练、测试数据中正负样本比例
prop.table(table(train_data$diagnosis))
##
## B M
## 0.6281407 0.3718593
prop.table(table(test_data$diagnosis))
##
## B M
## 0.6294118 0.3705882
数据建模
在R语言中,knn建模有多个包可以选择,常用的机器学习包是caret,集成了很多常用的机器学习算法。
library(caret)
# 设置10折交叉训练
control <- trainControl(method = 'cv',number = 10)
# knn模型训练
model <- train(diagnosis~.,train_data,
method = 'knn',
preProcess = c('center','scale'),
trControl = control,
tuneLength = 5)
- 通过
trainControl函数设置10折交叉训练,并传入到trControl参数中; - 通过
preProcess参数设置训练数据标准化处理; - 通过
tuneLength参数设置k取值个数,模型以此进行参数网格搜索调优。 - 模型训练评价指标,分类问题默认为准确率。
查看训练好的模型,可知模型的准确率都超过了95%,且最优模型的k值为5。
model
## k-Nearest Neighbors
##
## 398 samples
## 30 predictor
## 2 classes: 'B', 'M'
##
## Pre-processing: centered (30), scaled (30)
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 358, 358, 358, 359, 358, 359, ...
## Resampling results across tuning parameters:
##
## k Accuracy Kappa
## 5 0.9648077 0.9233640
## 7 0.9623077 0.9178105
## 9 0.9622436 0.9170249
## 11 0.9597436 0.9116195
## 13 0.9622436 0.9168826
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 5.
模型预测
利用训练好的模型,可以对测试数据进行预测,来检验模型的性能。一般通过混淆矩阵来评估分类模型的性能,通过confusionMatrix函数实现。
# 测试数据真实值
truth <- test_data$diagnosis
# 测试数据预测值
pred <- predict(model,newdata = test_data)
# 计算混淆矩阵
confusionMatrix(table(pred,truth))
## Confusion Matrix and Statistics
##
## truth
## pred B M
## B 107 9
## M 0 54
##
## Accuracy : 0.9471
## 95% CI : (0.9019, 0.9755)
## No Information Rate : 0.6294
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.8831
##
## Mcnemar's Test P-Value : 0.007661
##
## Sensitivity : 1.0000
## Specificity : 0.8571
## Pos Pred Value : 0.9224
## Neg Pred Value : 1.0000
## Prevalence : 0.6294
## Detection Rate : 0.6294
## Detection Prevalence : 0.6824
## Balanced Accuracy : 0.9286
##
## 'Positive' Class : B
##
从预测的结果来看,模型的准确率达到了94.71%,模型有良好的泛化能力,说明出knn算法的性能不错;同时,可以看出模型也错分了9个负样本,模型也有进一步优化的空间。总体来说,knn模型表现良好,不过在实际工程应用中,一次训练的模型一般不能直接上线部署,需要多次试验,充分验证模型的准确率和泛化能力,比如可以在数据切割阶段,根据实际数据情况,保留更多的测试数据。