贪心算法类典型题目的常规思路—Leetcode-thinking_record06
目录
分糖果(Easy)
总体思路
细节设计
代码实现
经验总结
摇摆序列(Medium)
总体思路
细节设计
代码实现
经验总结
移除K个数字(Medium)
总体思路
细节设计
代码实现
经验总结
跳跃游戏Ⅰ(Medium)
总体思路
细节设计
代码实现
经验总结
跳跃游戏Ⅱ(Medium)
总体思路
细节设计
代码实现
经验总结
射击气球(Medium)
总体思路
细节设计
代码实现
经验总结
最优加油方法(Hard)
总体思路
细节设计
代码实现
经验总结
贪心法精髓:遵循某种规律,不断贪心的选取当前最优策略的算法设计方法。
只要保证当前环节结果是最优的,那么就能保证整个过程都是最优的!
一般来说,贪心算法适用的题目都不会特别的长,而且特别容易理解题意,也不需要特别复杂的数据结构,所以特别能考察算法的思维方式。
贪心算法的难度一般都不会特别难,一般只有跟堆啊或者其他比较复杂的数据结构结合在一起的时候,才会变的复杂点儿。
分糖果(Easy)
LeetCode 455.Assign Cookies
已知一些孩子和一些糖果,每个孩子有需求因子g,每个糖果有大小s,当某个糖果的大小s>=某个孩子的需求因子g时,代表该糖果可以满足该孩子;求使用这些糖果,最多能满足多少孩子?(注意,某个孩子最多只能用1个糖果满足)
例如,需求因子数组g = [5, 10,2, 9, 15, 9]; 糖果大小数组s = [6, 1, 20, 3, 8];最多可以满足3个孩子。
总体思路
先思考两个问题:
- 当某个函数可以被多个糖果满足时,是否需要优先用某个糖果满足这个孩子?
- 当某个糖果可以满足多个孩子时,是否需要优先满足某个孩子?
那么如果以“让更多孩子得到满足”为核心目标,就会发现有如下规律:
- 某个糖果如果不能满足某个孩子,则该糖果也一定不能满足需求因子更大的孩子。如,糖果1(s=1)不能满足孩子1(g=2),则不能满足孩子2、孩子3、...、孩子7;糖果2(s=3)不能满足孩子2(g=5),则不能满足孩子3、孩子4、...、孩子7....
- 某个孩子可以用更小的糖果满足时,就没必要用更大糖果满足,因为可以保留更大的糖果去满足需求因子更大的孩子(贪心算法的精髓),如,孩子1(g=2),可以被糖果2(s=3)满足,则没必要用糖果3、糖果4、糖果5满足;孩子2(g=5),可以被糖果3(s=6)满足,则没必要用糖果4、糖果5满足。
- 孩子的需求因子更小则其更容易被满足,故优先从需求因子小的孩子尝试,用某个糖果满足一个较大需求因子的孩子或满足一个较小需求因子的孩子效果是一样的(最终满足的总理是不变的)(贪心算法的精髓)
细节设计
对需求因子数组g与糖果大小数组s进行从小到大的排序。
按照从小到大的顺序使用各糖果尝试是否可满足某个孩子,每个糖果只尝试1次;若尝试成功,则换下一个孩子尝试;直到发现没更多的孩子或者没更多的糖果,循环结束。
代码实现
#include
#include
#include
class Solution {
public:
int findContentChildren(std::vector& g, std::vector& s) {
std::sort(g.begin(), g.end());
std::sort(s.begin(), s.end());
int child = 0;
int cookie = 0;
while(child < g.size() && cookie < s.size()){
if (g[child] <= s[cookie]){
child++;
}
cookie++;
}
return child;
}
};
int main(){
Solution solve;
std::vector g;
std::vector s;
g.push_back(5);
g.push_back(10);
g.push_back(2);
g.push_back(9);
g.push_back(15);
g.push_back(9);
s.push_back(6);
s.push_back(1);
s.push_back(20);
s.push_back(3);
s.push_back(8);
printf("%d\n", solve.findContentChildren(g, s));
return 0;
} 经验总结
摇摆序列(Medium)
LeetCode 376.Wiggle Subsequence
一个整数序列,如果两个相邻元素的差恰好正负(负正)交替出现,则该序列被称为摇摆序列。一个小于2个元素的序列直接为摇摆序列。
例如:
序列[1,7,4,9,2,5],相邻元素的差(6,-3,5,-7,3),该序列为摇摆序列。
序列[1,4,7,2,5](3,3,-5,3)、[1,7,4,5,5](6,-3,1,0)不是摇摆序列。
给一个随机序列,求这个序列满足摇摆序列定义的最长子序列的长度。
例如:
输入[1,7,4,9,2,5],结果为6;输入[1,17,5,10,13,15,10,5,16,8],结果为7([1,17,10,13,10,16,8]);输入[1,2,3,4,5,6,7,8,9],结果为2。
总体思路
以[1,17,5,10,13,15,10,5,16,8]为例,当观察后会发现,这个序列整体不是摇摆序列,但是,
如果只看前六位,摇摆序列的第四位备选项有三个:10、13、15,那到底那个会使这个摇摆序列变的最长吗?
这里面用到贪心算法的地方就在于,要保证站在当前元素,应该尽可能使下个元素的摇摆序列的几率更大,那就应该选“摇摆幅度”最大的那个。
当序列有一段连续的递增(或递减)时,为形成摇摆子序列,我们只需要保留这段连续的递增(或递减)的首尾元素,这样更可能使得尾部的后一个元素成为摇摆子序列的下一个元素。
其中 ,用红框标住的,就是保证序列长度最长的摇摆序列。可以发现,摇摆序列的每个元素,应该选择在摇摆的转折点,这样可以仅最大保证能够入选下一个摇摆序列的元素多。
细节设计
代码实现
#include
#include
class Solution {
public:
int wiggleMaxLength(std::vector& nums) {
if (nums.size() < 2){
return nums.size();
}
static const int BEGIN = 0;
static const int UP = 1;
static const int DOWN = 2;
int STATE = BEGIN;
int max_length = 1;
for (int i = 1; i < nums.size(); i++){
switch(STATE){
case BEGIN:
if (nums[i-1] < nums[i]){
STATE = UP;
max_length++;
}
else if (nums[i-1] > nums[i]){
STATE = DOWN;
max_length++;
}
break;
case UP:
if (nums[i-1] > nums[i]){
STATE = DOWN;
max_length++;
}
break;
case DOWN:
if (nums[i-1] < nums[i]){
STATE = UP;
max_length++;
}
break;
}
}
return max_length;
}
};
int main(){
std::vector nums;
nums.push_back(1);
nums.push_back(17);
nums.push_back(5);
nums.push_back(10);
nums.push_back(13);
nums.push_back(15);
nums.push_back(10);
nums.push_back(5);
nums.push_back(16);
nums.push_back(8);
Solution solve;
printf("%d\n", solve.wiggleMaxLength(nums));
return 0;
} 经验总结
- 在选择当前节点的时候,尽可能使满足成为下一个节点的条件的备选节点增多。
移除K个数字(Medium)
LeetCode 402.Remove K Digits
已知一个使用字符串表示的非负整数num,将num中的k个数字移除,求移除k个数字后,可以获得的最小的可能的新数字。
输入:num = “1432219”,k=3
在去掉3个数字后得到的很多很多可能里,如1432、4322、219、1219、1229。。。;
去掉数字4、3、2得到的1219最小!
总体思路
经过初步分析,这种问题肯定不能通过枚举法来求解,因为遇到的数字可能是非常大的。根据经验这是一个线性思路去求解的,无非要么是贪心算法要么是动态规划。
总结规律可以发现: 如果需要去掉某位数字,为了使得到的新数字最小,需要尽可能让得到的新数字优先最高位最小,其次,次高位最小,其次,次次高位最小,依次类推。那么,从高位向低位遍历,如果对应的数字大于下一位数字,则把该位数字去掉,得到的数字最小!
但是,问题又来了,那总不能要求去掉k个数字,就循环k次吧,那样的话时间复杂度是非常大的,所以,有没有什么办法在降低时间复杂度的情况下,又可以保证上面思路的实现呢?
这就要用到上篇博客中所提及的栈模型了,为啥栈模型可以呢?因为栈独特的先进后出模型,把所有位数字都放进栈中,最高位最先进去放在栈的最底下,后面进去的数字会跟放进去的最高位做比较,如果大于上一次放进去的最高位数字,就把当前的数字给去掉,然后计数加一,如果小于上一次放进去的最高位数字,就把上一次放进去的最高位数字给去掉,然后计数加一,重复这样的操作,直到计数达到设定的k值,停下。
另外,需要考虑数值为0的时候的边界值情况;当所有数字都扫描完后,k仍然大于0的时候,应该如何处理;如何将最后的结果存储为字符串并返回。
细节设计
代码实现
#include
#include
#include
class Solution {
public:
std::string removeKdigits(std::string num, int k) {
std::vector S;
std::string result = "";
for (int i = 0; i < num.length(); i++){
int number = num[i] - '0';
while(S.size() != 0 && S[S.size()-1] > number && k > 0){
S.pop_back();
k--;
}
if (number != 0 || S.size() != 0){
S.push_back(number);
}
}
while(S.size() != 0 && k > 0){
S.pop_back();
k--;
}
for (int i = 0; i < S.size(); i++){
result.append(1, '0' + S[i]);
}
if (result == ""){
result = "0";
}
return result;
}
};
int main(){
Solution solve;
std::string result = solve.removeKdigits("1432219", 3);
printf("%s\n", result.c_str());
std::string result2 = solve.removeKdigits("100200", 1);
printf("%s\n", result2.c_str());
return 0;
} 经验总结
- 通过从高位向低位遍历,每次去除当前位和下一位中数值较大的那个,来保证每次去掉的后,整体数字的值最小。
- 贪心法的简单之处在于,每道用贪心算法解决的题目,都可以看见每个环节最优,然后,重复对每个环节的操作,就可以保证整个过程的最优操作,但是,它的难点也在于,实现每个环节的最优的方法,各不相同,都需要对具体场景量身定做。
跳跃游戏Ⅰ(Medium)
LeetCode 55.Jump Game
一个数组存储了非负整型数据,数组中的第i个元素a[i],代表了可以从数组第i个位置最多向前跳跃a[i]步;已知数组各元素的情况下,求是否可以从数组的第0个位置跳跃到数组的最后一个元素的位置?
例如:
nums = [2,3,1,1,4],可以从nums[0]=2跳跃至nums[4]=4;
nums = [3,2,1,0,4],不可以从nums[0]=3跳跃至nums[4]=4。
总体思路
总结一下,每次保证跳到可覆盖距离中的,可跳位置最多的位置,可以保证到达最后位置,如果这都到达不了,那就说明无法到达了。
细节设计
代码实现
#include
#include
class Solution {
public:
bool canJump(std::vector& nums) {
std::vector index;
for (int i = 0; i < nums.size(); i++){
index.push_back(i + nums[i]);
}
int jump = 0;
int max_index = index[0];
while(jump < index.size() && jump <= max_index){
if (max_index < index[jump]){
max_index = index[jump];
}
jump++;
}
if (jump == index.size()){
return true;
}
return false;
}
};
int main(){
std::vector nums;
nums.push_back(2);
nums.push_back(3);
nums.push_back(1);
nums.push_back(1);
nums.push_back(4);
Solution solve;
printf("%d\n", solve.canJump(nums));
return 0;
} 经验总结
跳跃游戏Ⅱ(Medium)
LeetCode 45.Jump Game II
一个数组存储了非负整型数据,数组中的第i个元素a[i],代表了可以从数组第i个位置最多向前跳跃a[i]步;已知数组各元素的情况下,确认可以从第0位置跳跃到数组最后一个位置,求最少需要跳跃几次?
例如,nums=[2,3,1,1,4],从第0位置跳到第1位置,从第1位置跳至最后一个位置。
总体思路
每次跳到可选范围之内的,可以跳最多距离的位置。
细节设计
代码实现
#include
#include
class Solution {
public:
int jump(std::vector& nums) {
if (nums.size() < 2){
return 0;
}
int current_max_index = nums[0];
int pre_max_max_index = nums[0];
int jump_min = 1;
for (int i = 1; i < nums.size(); i++){
if (i > current_max_index){
jump_min++;
current_max_index = pre_max_max_index;
}
if (pre_max_max_index < nums[i] + i){
pre_max_max_index = nums[i] + i;
}
}
return jump_min;
}
};
int main(){
std::vector nums;
nums.push_back(2);
nums.push_back(3);
nums.push_back(1);
nums.push_back(1);
nums.push_back(4);
Solution solve;
printf("%d\n", solve.jump(nums));
return 0;
} 经验总结
- 保证每次跳跃的距离最大
射击气球(Medium)
LeetCode 452.Minimum Number of Arrows to Burst Balloons
已知在一个平面上有一定数量的气球,屏幕可以看作一个坐标系,在平面的x轴的不同位置弓箭手向y轴方向射箭,弓箭可以向y轴走无穷远;给定气球的宽度xstart<=x<=xend,问至少需要多少弓箭手,将全部气球打爆?
例如:四个气球:[[10,16],[2,8],[1,6],[7,12]],至少需要2个弓箭手。
总体思路
细节设计
代码实现
#include
#include
#include
bool cmp(const std::pair &a, const std::pair &b) {
return a.first < b.first;
}
class Solution {
public:
int findMinArrowShots(std::vector >& points) {
if (points.size() == 0){
return 0;
}
std::sort(points.begin(), points.end(), cmp);
int shoot_num = 1;
int shoot_begin = points[0].first;
int shoot_end = points[0].second;
for (int i = 1; i < points.size(); i++){
if (points[i].first <= shoot_end){
shoot_begin = points[i].first;
if (shoot_end > points[i].second){
shoot_end = points[i].second;
}
}
else{
shoot_num++;
shoot_begin = points[i].first;
shoot_end = points[i].second;
}
}
return shoot_num;
}
};
int main(){
std::vector > points;
points.push_back(std::make_pair(10, 16));
points.push_back(std::make_pair(2, 8));
points.push_back(std::make_pair(1, 6));
points.push_back(std::make_pair(7, 12));
Solution solve;
printf("%d\n", solve.findMinArrowShots(points));
return 0;
} 经验总结
- 尽可能使单次的效果最优
- 贪心算法最关键的是推算每次最优的策略
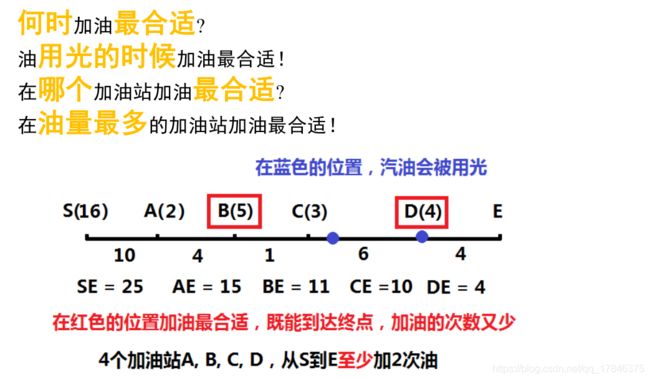
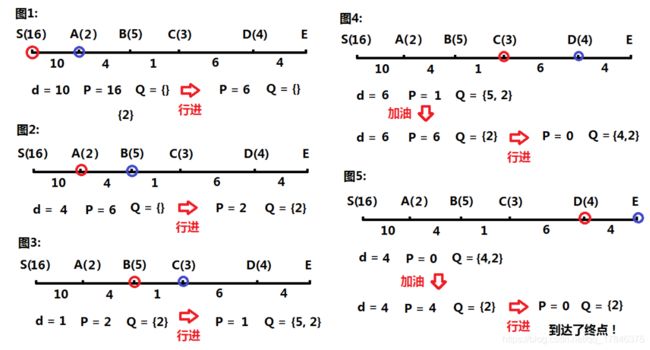
最优加油方法(Hard)
已知一条公路上,有一个起点与一个终点,这之间有n个加油站;已知从这n个加油站到终点的距离d与各个加油站可以加油的量l,起点位置至终点的距离L与起始时刻邮箱中汽油量P;假设使用1个单位的汽油即走1个单位的距离,油箱没有上限,最少加几次油,可以从起点开至终点?(如果无法到达终点,返回-1)
总体思路
细节设计
代码实现
#include
#include
#include
#include
bool cmp(const std::pair &a, const std::pair &b) {
return a.first > b.first;
}
int get_minimum_stop(int L, int P, std::vector > &stop){
std::priority_queue Q;
int result = 0;
stop.push_back(std::make_pair(0, 0));
std::sort(stop.begin(), stop.end(), cmp);
for (int i = 0; i < stop.size(); i++){
int dis = L - stop[i].first;
while (!Q.empty() && P < dis){
P += Q.top();
Q.pop();
result++;
}
if (Q.empty() && P < dis){
return -1;
}
P = P - dis;
L = stop[i].first;
Q.push(stop[i].second);
}
return result;
}
int main(){
std::vector > stop;
int N;
int L;
int P;
int distance;
int fuel;
scanf("%d", &N);
for (int i = 0; i < N; i++){
scanf("%d %d", &distance, &fuel);
stop.push_back(std::make_pair(distance, fuel));
}
scanf("%d %d", &L, &P);
printf("%d\n", get_minimum_stop(L, P, stop));
return 0;
} 经验总结
- 借用其他数据结构模型解决