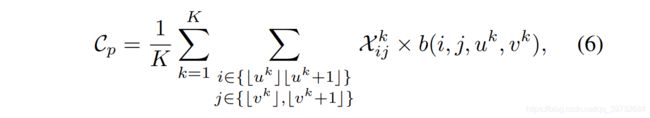小白科研笔记:深入理解SA-SSD中的Part-sensitive Warping机制
1. 前言
这篇博客将细致分析3D目标单阶段检测方法SA-SSD中的Part-sensitive warping机制(简称PS Warping)。
2. 代码上对PS Warping理解
论文上对PS Warping的介绍明明每个单词都认识,但是这些单词合在一起,就不明白说的什么意思了(笑哭),以及论文中公式(6)就是看不明白。那就先看看代码上PS Warping的实现(代码实现并不复杂,论文中的公式倒写的高大上)。如果你不想看代码,也可以跳过去看第三节。
class PSWarpHead(nn.Module):
# 该类初始化所需要的变量和它们的值
# grid_offsets = (0., 40.)
# featmap_stride=.4 => 0.4
# in_channels=256
# num_class=1 (应该是只针对车一类)
# num_parts=28
def __init__(self, grid_offsets, featmap_stride, in_channels, num_class=1, num_parts=49):
super(PSWarpHead, self).__init__()
self._num_class = num_class
out_channels = num_class * num_parts # 等于 28*1 = 28
# gen_grid_fn 是一个指向 gen_sample_grid 的句柄,字面理解是生成网格点
# 后面会深入分析它
self.gen_grid_fn = partial(gen_sample_grid, grid_offsets=grid_offsets, spatial_scale=1 / featmap_stride)
# 把输入通道为 256 的特征输出为通道为 28 的特征
self.convs = nn.Sequential(
nn.Conv2d(in_channels, out_channels, 3, 1, padding=1, bias=False),
nn.BatchNorm2d(out_channels, eps=1e-3, momentum=0.01),
nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, 1, 1, padding=0, bias=False)
)
# x 是 Neck 中的 BEVNet 的 conv6 的输出,张量尺寸为 [B, 256, 200, 176]
# guided_anchors 是所有 Anchors 中跟网络初始输出的预测 Box 相重叠那一部分
# guided_anchors 是 [B,N,7] 的张量, N 表示 anchor 的数量,
# 7 表示 xyzlwh 以及水平转角 theta,这七个参数
def forward(self, x, guided_anchors, is_test=False):
x = self.convs(x) # 张量尺寸为 [B, 28, 200, 176],称之为 confidence map
bbox_scores = list()
# 遍历每一个批次中的 guided_anchors,i 表示批次序号
# ga 是 [N,7] 的张量
for i, ga in enumerate(guided_anchors):
# 如果这个批次没有 guided anchor,就输出一个零值张量,尺寸跟 x 一样
if len(ga) == 0:
bbox_scores.append(torch.empty(0).type_as(x))
continue
# ga[:, [0, 1, 3, 4, 6]] 是 [N,5] 的张量
# 指 BEV 视图下的 Anchors,xy 和 lw 以及 水平转角 theta
# 在 BEV 视图下,每个 anchor 是一个矩形区域,
# 而 gen_grid_fn 是提取这个矩形区域内的栅格采样点
# xs, ys 分别是矩形区域内的栅格采样点在 x 和 y 轴坐标,是 [4*7, N] 张量
(xs, ys) = self.gen_grid_fn(ga[:, [0, 1, 3, 4, 6]])
# 提取这个批次下的特征图,im 是 [1, C, 200, 176] 的张量
im = x[i]
# 在每个 anchor 内的栅格采样点中插值出特征图中的特征向量,是 [N, C, w, h]
out = bilinear_interpolate_torch_gridsample(im, xs, ys)
# 以第一个维度做平均,score 是一个标量,返回每个 anchor 中所有采样点对应特征之平均值
score = torch.mean(out, 0).view(-1)
bbox_scores.append(score)
# 如果是模型学习阶段,就只输出 bbox_scores
if is_test:
return bbox_scores, guided_anchors
else:
return torch.cat(bbox_scores, 0)
上述代码中需要先了解gen_grid_fn的含义。话不多说看源码:
# box 是 [N,5] 的张量,表示 BEV 视图下的 Anchors
# window_size=(4, 7),4 对应论文中的 K 值吗?
# grid_offsets = (0., 40.)
# spatial_scale = 1/0.4 = 2.5
# gen_sample_grid 用于生成 bev anchor 下 window_size 个均匀网格点
def gen_sample_grid(box, window_size=(4, 7), grid_offsets=(0, 0), spatial_scale=1.):
N = box.shape[0]
win = window_size[0] * window_size[1]
xg, yg, wg, lg, rg = torch.split(box, 1, dim=-1) # 把 [N,5] 拆分为 5 个 [N,1]
xg = xg.unsqueeze_(-1).expand(N, *window_size) # 维度扩展为 [N,4,7]
yg = yg.unsqueeze_(-1).expand(N, *window_size) # 维度扩展为 [N,4,7]
rg = rg.unsqueeze_(-1).expand(N, *window_size) # 维度扩展为 [N,4,7]
cosTheta = torch.cos(rg) # cos(\theta) [N,1]
sinTheta = torch.sin(rg) # sin(\theta) [N,1]
# torch.linspace(-.5, .5, window_size[0]) 指在 [-0.5,0.5] 平均分为 window_size[0] 份
# type_as 表示指定张量数据类型,比如 float
# torch.linspace(-.5, .5, window_size[0]) = [-0.5000, -0.1667, 0.1667, 0.5000]
# torch.linspace(-.5, .5, window_size[1]) = [-0.5000, -0.3333, -0.1667, 0.0000, 0.1667, 0.3333, 0.5000]
# xx = [1,4] * [N,1] = [N,4] 张量
xx = torch.linspace(-.5, .5, window_size[0]).type_as(box).view(1, -1) * wg
yy = torch.linspace(-.5, .5, window_size[1]).type_as(box).view(1, -1) * lg
xx = xx.unsqueeze_(-1).expand(N, *window_size) # 维度扩展为 [N,4,7]
yy = yy.unsqueeze_(1).expand(N, *window_size)
x=(xx * cosTheta + yy * sinTheta + xg) # 生成 4*7 网格点,BEV anchor 所覆盖的网格点
y=(yy * cosTheta - xx * sinTheta + yg)
x = (x.permute(1, 2, 0).contiguous() + grid_offsets[0]) * spatial_scale
y = (y.permute(1, 2, 0).contiguous() + grid_offsets[1]) * spatial_scale
# 输出张量是 [28, N],表示 4*7 网格点在 x 和 y 轴上的坐标
return x.view(win, -1), y.view(win, -1)
3. 理论上对PS Warping理解
读懂上述代码,差不多就对论文中的PS Warping就能理解了。我尽量以通俗易懂的语言说明此过程计算。论文中的计算公式如下所示:
对于一个3D候选框,它对应目标的置信度为 C p C_p Cp。该3D候选框可以压缩为一个BEV视图下的2D候选框。然后在该2D候选框中均匀采集 K K K个点。在代码中, K = 4 × 7 = 28 K=4\times7=28 K=4×7=28,相当于在2D候选框中采集 4 × 7 4\times 7 4×7阵列个点。然后我想提取这些采样点在BEV特征图下的特征向量。
BEV视图的尺寸是 H × W H\times W H×W,在代码中是 1600 × 1408 1600 \times 1408 1600×1408。而BEV特征图的尺寸是 h × w h \times w h×w,在代码中是 200 × 176 200 \times 176 200×176。BEV特征图比BEV视图的尺寸小了整整八倍,即 h H = w W = 1 8 \frac{h}{H}=\frac{w}{W}=\frac{1}{8} Hh=Ww=81。所以说这些采样点的坐标必须要缩小八倍,才能在BEV特征图上找到相应的特征向量。
举个例子,比如说第 k k k个采样点在BEV视图下的坐标是 ( x k , y k ) (x_k,y_k) (xk,yk)。该采样点在BEV特征图下对应坐标应该是 ( u k , v k ) (u_k,v_k) (uk,vk),即 ( x k ∗ h H , y k ∗ w W ) (x_k*\frac{h}{H},y_k*\frac{w}{W}) (xk∗Hh,yk∗Ww)。这就存在一个问题,就是 u k u_k uk可能不是一个整数。比如说 u k = 1.2 u_k=1.2 uk=1.2, v k = 3.8 v_k=3.8 vk=3.8。我们希望用它周围区域的特征插值出 ( u k , v k ) (u_k,v_k) (uk,vk)对应的特征。常见的方法就是双线性插值。
对双线型插值而言,首先要得到 ( u k , v k ) (u_k,v_k) (uk,vk)邻域四个点的坐标,即 ( ⌊ u k ⌋ , ⌊ v k ⌋ ) (\lfloor u_k \rfloor, \lfloor v_k \rfloor) (⌊uk⌋,⌊vk⌋), ( ⌊ u k ⌋ , ⌊ v k + 1 ⌋ ) (\lfloor u_k \rfloor, \lfloor v_k+1 \rfloor) (⌊uk⌋,⌊vk+1⌋), ( ⌊ u k + 1 ⌋ , ⌊ v k ⌋ ) (\lfloor u_k+1 \rfloor, \lfloor v_k \rfloor) (⌊uk+1⌋,⌊vk⌋), ( ⌊ u k + 1 ⌋ , ⌊ v k + 1 ⌋ ) (\lfloor u_k+1 \rfloor, \lfloor v_k+1 \rfloor) (⌊uk+1⌋,⌊vk+1⌋)。对应上述公式中 i i i和 j j j的索引范围。按照前文的例子,就是 ( 1 , 3 ) (1,3) (1,3), ( 1 , 4 ) (1,4) (1,4), ( 2 , 3 ) (2,3) (2,3), ( 2 , 4 ) (2,4) (2,4),这四个坐标。然后这四个坐标点 ( i , j ) (i,j) (i,j)到目标点 ( u k , v k ) (u_k,v_k) (uk,vk)的权值就是 b ( i , j , u k , v k ) b(i,j,u_k,v_k) b(i,j,uk,vk)。而这四个坐标点在BEV特征图上的特征就是 X i j k X_{ij}^k Xijk。
总而言之,计算 C p C_p Cp公式其实是双线性插值的紧凑数学表达而已。个人感觉,PS warping应该是ROIAlign的一种变形吧。
PS:代码中的张量尺寸可能有的弄错了。