（系列笔记）27.主成分分析——PCA（下）

PCA——用 SVD 实现 PCA

PCA 优化算法

PCA的优化算法目的是优化它的目标函数：

算法一，拉格朗日乘子法：

令：

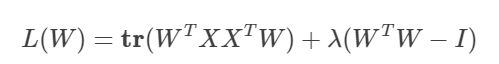
然后对W求导，并令导函数为0可得：

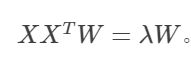
这是一个标准的特征方程求解问题，只需要对协方差矩阵$X{X}^T$进行特征值分解，将求得的特征值排序：${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_d$，再取前$d^{\prime }$个特征对应的特征向量构成$W=(w_1,w_2,...,w_{d^{\prime }})$即可。这样就求出了W，即为主成分分析的解。

算法描述：
【输入】：

• d维空间中n个样本数据的集和D={$x^{(1)},x^{(2)},...,x^{(n)}$}
• 低维空间的维数$d^{\prime }$，这个数值通常由用户指定。

【过程】：

1. 对所有原始样本做中心话：$x^{(i)}:=x^{(i)}-\frac{1}{n}{\sum }_{i=1}^n{x}^{(i)}$
2. 计算样本的协方差矩阵：$X{X}^T$
3. 协方差矩阵$X{X}^T$进行特征值分解；
4. 取最大的$d^{\prime }$个特征值对应的特征向量$w^{(1)},w^{(2)},...,w^{(d^{\prime })}$

【输出】：
$W=(w^{(1)},w^{(2)},...,w^{(d^{\prime })})$

算法二

上述求解过程可以换一个角度来看。

先对协方差矩阵${\sum }_{i=1}^n{x}^{(i)}{x^{(i)}}^T$做特征值分解，取最大特征值对应的特征向量$w_1$； 再对${\sum }_{i=1}^n{x}^{(i)}{x^{(i)}}^T-{\lambda }_1{w}_1{w}_1^T$做特征值分解，取其最大特征值对应的特征向量$w_2$；以此类推。因为 W 的各个分量正交，因此${\sum }_{i=1}^n{x}^{(i)}{x^{(i)}}^T={\sum }_{j=1}^d{\lambda }_1{w}_1{w}_1^T$

故而解法二和解法一等价。

PCA 的作用

PCA 将 d 维的原始空间数据转换成了d′ 维的新空间数据，无疑丧失了部分数据。

根据上面讲的算法我们知道，经过 PCA 后，原样本集协方差矩阵进行特征值分解后，倒数(d−d′) 个特征值对应的特征向量被舍弃了。

因为舍弃了这部分信息，导致的结果是：

• 样本的采样密度增大——这是降维的首要动机；]
• 最小的那部分特征值所对应的特征向量往往与噪声有关，舍弃它们有降噪的效果。

奇异值分解（Singular Value Decomposition, SVD）

SVD 是线性代数中一种重要的矩阵分解方法，在信号处理、统计学等领域有重要应用。

SVD的三个矩阵

我们先来看看 SVD 方法本身。假设 M 是一个 m×n 阶实矩阵，则存在一个分解使得：


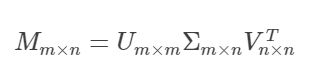
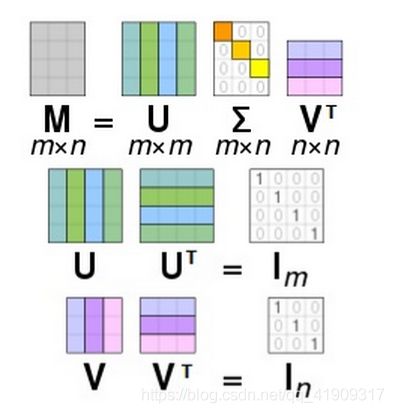
其中，Σ 是一个m×n 的非负实数对角矩阵，Σ 对角线上的元素是矩阵 M 的奇异值：

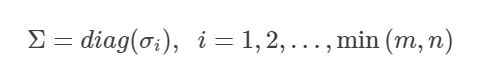
注意：对于一个非负实数 σ 而言，仅当存在 m 维的单位向量 u 和 n 维的单位向量v，它们和 M 及 σ 有如下关系时：$Mv=\sigma u$ 且 $M^{T}u=\sigma v$
我们说 σ 是 M 矩阵的奇异值，向量 u 和 v 分别称为 σ 的左奇异向量和右奇异向量。
一个 m×n 的矩阵至多有 min(m,n) 个不同的奇异值

U是一个m×m的酉矩阵，它是一组由 M 的左奇异向量组成的正交基：$U=(u_1,u_2,...,u_m)$。

它的每一列$u_i$都是$\sum$中对应序号的对角值${\sigma }_i$关于M的左奇异向量。

V是一个n×n的酉矩阵，它是一组由 M 的右奇异向量组成的正交基：$V=(v_1,v_2,...,v_n)$。

它的每一列$u_i$都是$\sum$中对应序号的对角值${\sigma }_i$关于M的右奇异向量。

酉矩阵：若一个n×n的实数方阵U满足$U^{T}U=U{U}^T=I_n$，则称为酉矩阵。

三个矩阵间的关系

我们这样看来：

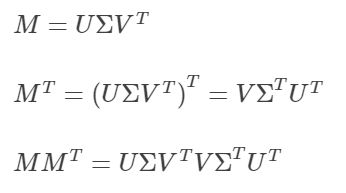
又因为U和V都是酉矩阵，所以：

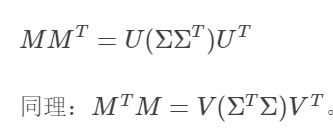
也就是说U的列向量是$M{M}^T$的特征向量，V的列向量是$M^{T}M$的特征向量；而$\sum$的对角元素，是M的奇异值，也是$M{M}^T$或者$M^{T}M$的非零特征值的平方根。

SVD的计算

手动计算过程：

1. 计算$M{M}^T$和$M^{T}M$；
2. 分别计算$M{M}^T$和$M^{T}M$的特征向量及其特征值；
3. 用$M{M}^T$的特征向量组成U，$M^{T}M$的特征向量组成V；
4. 对$M{M}^T$和$M^{T}M$的非零特征值求平方根，对应上述特征向量的位置，填入$\sum$的对角元。

更详细的过程可以看：http://web.mit.edu/be.400/www/SVD/Singular_Value_Decomposition.htm

用 SVD 实现 PCA

所谓降维度，就是按照重要性排列现有特征，舍弃不重要的，保留重要的。

上面讲了 PCA 的算法，很关键的一步就是对协方差矩阵进行特征值分解，不过其实在实践当中，我们通常用对样本矩阵 X 进行奇异值分解来代替这一步。

X 是原空间的样本矩阵，W 是投影矩阵，而 T 是降维后的新样本矩阵，有 $T=XW$。

我们直接对X做SVD，得到：$T=XW=U\sum W^{T}W$

因为W是标准正交基组成的矩阵，因此：$T=U\sum W^{T}W=U\sum$。

我们选矩阵U前d’列，和$\sum$左上角前d’×d’区域内的对角值，也就是前d’打的奇异值，然后直接降维：$T_{d^{\prime }}=U_{d^{\prime }}{\sum }_{d^{\prime }}$

这样做很容易解释其物理意义：样本数据的特征重要性程度既可以用特征值来表征，也可以用奇异值来表征。

动机也很清楚，当然是成本。直接做特征值分解需要先求出协方差矩阵，当样本或特征量大的时候，计算量很大。更遑论对这样复杂的矩阵做特征值分解的难度了。

而对矩阵M进行SVD时，直接对$M{M}^T$做特征值分解，要简单得多。

当然SVD算法本身也是一个接近$O(m^3)$（假设m>n）时间复杂度的运算，不过现在SVD的并行运算已经被实现，效率也因此提高不少。

直接用 SVD 降维

除了可以用于 PCA 的实现，SVD 还可以直接用来降维。

在现实应用中，SVD 也确实被作为降维算法大量使用。

有一些应用，直接用眼睛就能看得见。比如：用 SVD 处理图像，减少图片信息量，而又尽量不损失关键信息。

图片是由像素（Pixels）构成的，一般彩色图片的单个像素用三种颜色（Red、Green、Blue）描述，每一个像素点对应一个 RGB 三元值。一张图片可以看作是像素的二维点阵，正好可以对应一个矩阵。那么我们用分别对应 RGB 三种颜色的三个实数矩阵，就可以定义一张图片。

设$X_R,X_G,X_B$是用来表示一张图片的RGB数值矩阵，我们对其做SVD：

$X_R=U_R{\sum }_R{V}_R^T$

然后我们制定一个参数：$k,U_R$和$V_R$取前k列，形成新的矩阵$U_R^k$和$V_R^k$，${\sum }_R$取左上k×k的区域，形成新矩阵${\sum }_R^k$，然后用它们生成新的矩阵：

$X_R^{{}^{\prime }}=U_R^k{\sum }_R^k{(V_R^k)}^T$

对$X_G,X_B$做同样的事情，最后形成的$X_R^{\prime },X_G^{\prime },X_B^{\prime }$定义的图片，就是压缩了信息量后的图片。

如此处理后的图片尺寸未变，也就是说$X_R^{\prime },X_G^{\prime },X_B^{\prime }$与原本的$X_R,X_G,X_B$行列数一致，只不过矩阵承载的信息量变小了。
比如，$X_R$是一个m×n矩阵，那么$U_R$是一个m×m矩阵，${\sum }_R$是一个m×n矩阵，而$V_R^T$是一个n×n矩阵，$U_R^k$是一个m×k矩阵，${\sum }_R^k$是一个k×k矩阵，而${(V_R^k)}^T$是一个k×n矩阵,它们相乘的矩阵仍然是m×n矩阵。从数学上讲，经过 SVD 重构后的新矩阵，相对于原矩阵秩（Rank）下降了。

SVD & PCA 实例

压缩这张图

我们将分别尝试 SVD 和 PCA 两种方法。

SVD压缩图片

我们用 SVD 分解上面这张图片，设不同的 k 值，来看分解后的结果。

下面几个结果的 k 值分别是：100、50、20和5。很明显，k 取 100 的时候，损失很小，取 50 的时候还能看清大致内容，到了 20 就模糊得只能看轮廓了，到了 5 则是一片条纹。

code

    import os
    import threading

    import numpy as np
    import matplotlib.pyplot as plt
    import matplotlib.image as mpimg
    import sys

    def svdImageMatrix(om, k):
        U, S, Vt = np.linalg.svd(om)
        cmping = np.matrix(U[:, :k]) * np.diag(S[:k]) * np.matrix(Vt[:k,:])    
        return cmping

    def compressImage(image, k):
        redChannel = image[..., 0]
        greenChannel = image[..., 1]
        blueChannel = image[..., 2]

        cmpRed = svdImageMatrix(redChannel, k)
        cmpGreen = svdImageMatrix(greenChannel, k)
        cmpBlue = svdImageMatrix(blueChannel, k)

        newImage = np.zeros((image.shape[0], image.shape[1], 3), 'uint8')

        newImage[..., 0] = cmpRed
        newImage[..., 1] = cmpGreen
        newImage[..., 2] = cmpBlue

        return newImage

    path = 'liye.jpg'
    img = mpimg.imread(path)

    title = "Original Image"
    plt.title(title)
    plt.imshow(img)
    plt.show()

    weights = [100, 50, 20, 5]

    for k in weights:
        newImg = compressImage(img, k)

        title = " Image after =  %s" %k
        plt.title(title)
        plt.imshow(newImg)
        plt.show()    

        newname = os.path.splitext(path)[0] + '_comp_' + str(k) + '.jpg'
        mpimg.imsave(newname, newImg)

PCA压缩图片

使用from sklearn.decomposition import PCA

过程部分，只要将上面代码中的svdImageMatrix() 替换为如下 pca() 即可：

    def pca(om, cn):

        ipca = PCA(cn).fit(om)
        img_c = ipca.transform(om)

        print img_c.shape
        print np.sum(ipca.explained_variance_ratio_)

        temp = ipca.inverse_transform(img_c)
        print temp.shape

        return temp

cn 对应 sklearn.decomposition.PCA 的 n_components 参数，指的是 PCA 算法中所要保留的主成分个数 n，也就是保留下来的特征个数 n。

我们仍然压缩四次，具体的 cn 值还是 [100, 50, 20, 5]。

从运行的结果来看，和 SVD 差不多。

其实好好看看 sklearn.decomposition.PCA 的代码，不难发现，它其实就是用 SVD 实现的。