【智算之道】2020智算之道复赛题解

发挥不好的一场

只包含ABCD ，E 过两日会update！

A.数字

签到题吧，枚举前三位即可

Code:

/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(3)
#include 
using namespace std;
typedef long long ll;
ll n,m,p;
int main()
{
    read(n);read(m);
    int ans = 0;
    ll x = 1;
    while(x<=n) x*=10;
    for(register int i=100;i<=999;i++){
        ll temp = (i*x+n);
        if((temp/m)*m == temp) ans++;
    }
    printf("%d\n",ans);
    return 0;
}
/***
***/

B.网格

贪心的考虑一下

如果平常走费用少，绝对会平常走

否则尽可能多的去走魔法方格

多的魔法方格就走一个xy都哦严格递增的最长上升子序列

Code:

ll n,m,p;
struct node{
    ll x,y;
}q[maxn];
bool operator<(node a,node b){
    if(a.x == b.x) return a.y < b.y;
    return a.x < b.x;
}
int st[maxn];
int main()
{
    ll a,b;
    read(n);read(m);read(a);read(b);
    for(register int i=1;i<=m;i++){
        read(q[i].x);
        read(q[i].y);
    }
    if(2*a <= b)
        printf("%lld\n",(2*n-1)*a);
    else{
        sort(q+1,q+1+m);
        int s = 0;
        for(int i=1;i<=m;i++){
            int k = i;
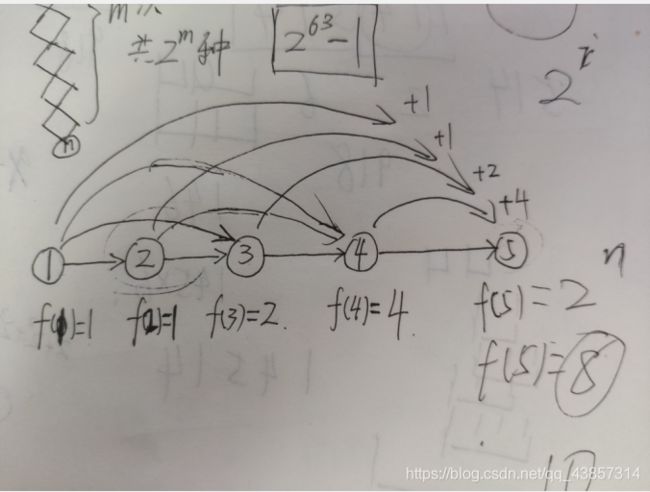
            if(!s||st[s]

C.有向无环图

考虑连成一个无向图

令fi代表从1~i的路径数量

然后你就会发现一些奇特的性质..

/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(3)
#include 
inline bool read(ll &num)
{char in;bool IsN=false;
    in=getchar();if(in==EOF) return false;while(in!='-'&&(in<'0'||in>'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
int cnt = 2;
ll n,m,p;
struct No{
    int x,y;
};
vectorres;
int main()
{
    ll K,N;scanf("%llu%llu",&K,&N);
    __int128 temp = 1;
    while(temp>(i-2)&1)==0) res.push_back(No{i,cnt});
    }
    printf("%d %d\n",cnt,res.size());
    int sz = res.size();
    for(int i=0;i

D.分数

考虑首先每一个绝对会被质因子筛去一次

对于剩下的只有质因子的幂次

所以直接欧拉筛即可

8e7能开还是狠莽的..

Code:

/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(3)
#include 
ll n,m,p;
bool vis[maxn];
int prime[12000000],f[maxn];
int cnt = 0;
void set_prime()
{
    for(register int i=2;imod) a%=mod;
        }
        else if(f[i]){
            a = (a*f[i]+b);
            if(a>mod) a%=mod;
        }
    }
    printf("%lld\n",a);
    return 0;
}
/***
10 2
1 2
2 3
3 4
4 10
2 5
5 6
6 7
7 8
8 9
***/

总结：

rk53..没关系

不以弱于强者而自卑

不以强于弱者而骄傲

更重要的

不能被失落的低谷吞噬。