洛谷——P2241 统计方形（数据加强版）（数学+暴力枚举）

洛谷——P2241 统计方形（数据加强版）

题目

题目背景

1997年普及组第一题

题目描述

有一个n*m方格的棋盘，求其方格包含多少正方形、长方形

输入格式

n,m因为原来数据太弱，现规定m小于等于5000，n小于等于5000（原来是100,100）

输出格式

方格包含多少正方形、长方形

输入输出样例

输入 #1

2 3

输出 #1

8 10

解题思路

  网上有很多更简练的解题思路，这里介绍一种通俗易懂的。
  我们假设一个长方形长为 x , 宽为 y ,那么在长为 n ，宽为 m 的矩形中，其存在数量为 (n-x+1)*(m-y+1)个。是不是很懵，哎，哎，哎，不如来画个图吧。

 （原谅我惨不忍睹的画画技能）

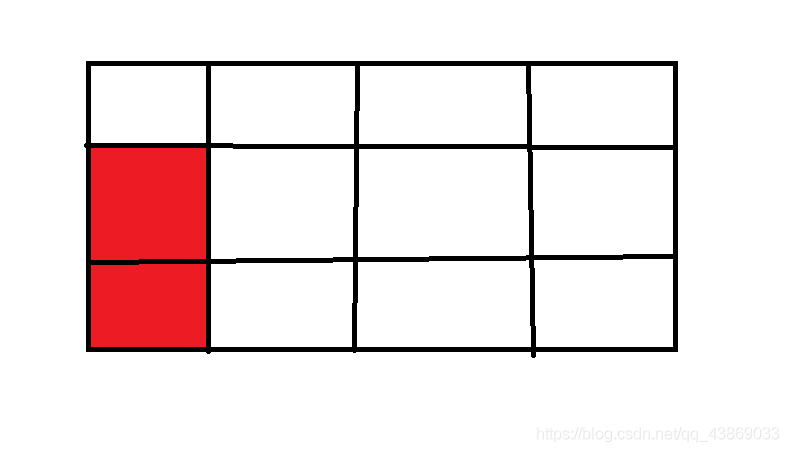
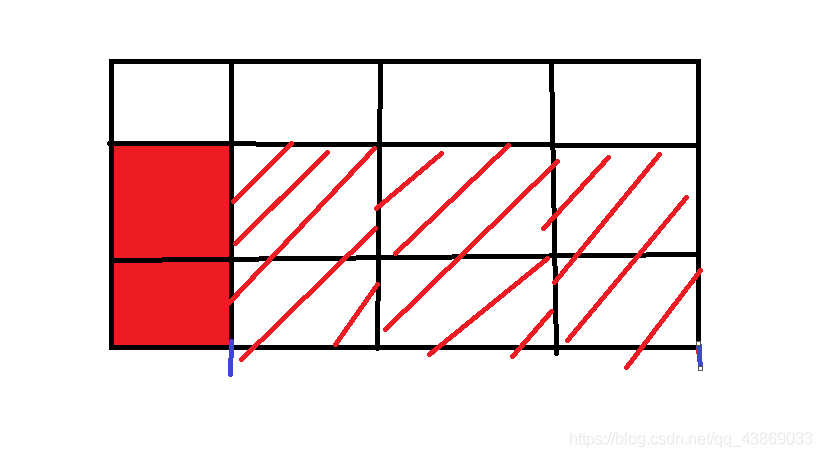
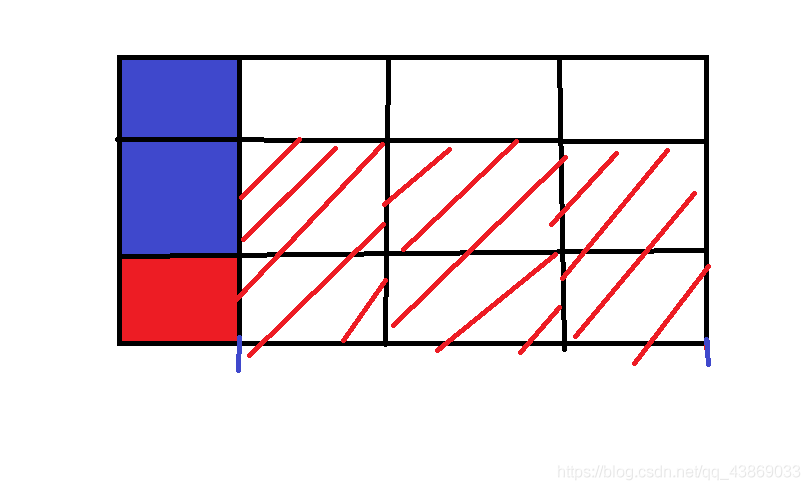
  假设大矩形 n=4 ,m=3 ，我们要求的小矩形 x=1, y=2。我们可以看到在两
个蓝线段之间的部分允许红色小矩形任意向右平移，那么他在横方向上总共有 4-1+1 =
4个可选择的位置，也就是横方向上允许存在4个不同的该矩形，同理，在纵方向上允许存在3-2+1=2个该种矩形，所以一共允许存在2*4=8 个该矩形。那么我们只要将 x 从 1 枚举到 n， y 从 1 枚举到 m , 即可得到各种边长下矩形允许存在数量 ，然后加和即可得到所有矩形允许数量，但需要注意的是，正方形是特殊的矩形，所以当 x=y 时即为正方形允许的存在数量。（数据可能很大，记得用 long long）

AC代码

#include 
using namespace std;
typedef long long ll;
int main()
{
    int n,m;
    cin>>n>>m;

    ll sq=0;
    ll rec=0;
    for(int i=0;i<n;i++)     		//从0开始就可以将+1省略
    {
        for(int j=0;j<m;j++)        //从0开始就可以将+1省略
        {
            if(i==j)
            {
                sq=sq+(m-i)*(n-i);
            }
            else
            {
                rec=rec+(n-i)*(m-j);
            }
        }
    }
    cout<<sq<<" "<<rec<<endl;
    return 0;
}