2019 ICPC 南京区域赛 - C Digital Path（多段图DP）

题目链接

---

前言：时隔八个多月，终于学了DP，前来补题

首先看到这个题，容易想到从最左列到最右列的最短(长)路的问题，明显是DP。唯一的区别是本题可能有多个起点，因为是求长度大于等于$4$的序列个数，那么我们设$d(i,j,k)$代表当前坐标$(i,j)$，以它为起点的长度为$k$的序列个数，大于$4$的也归为$4$中。然后我一开始写的dfs是这样的：

void dfs(int x,int y){
    if(vis[x][y]) return;
    vis[x][y]=1;
    d[x][y][1]=1LL;
    for(int i=0;i<4;i++){
        int xx=x+dx[i],yy=y+dy[i];
        if(xx<0 || xx>=r || yy<0 || yy>=c) continue;
        if(a[x][y]+1==a[xx][yy]){
            dfs(xx,yy);
            d[x][y][2]=(d[x][y][2]+d[xx][yy][1])%Mod;
            d[x][y][3]=(d[x][y][3]+d[xx][yy][2])%Mod;
            d[x][y][4]=(d[x][y][4]+max(d[xx][yy][4],d[xx][yy][3]))%Mod;

        }
    }
}

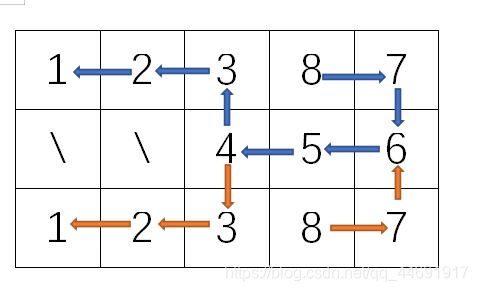
看起来这个函数没有问题，但是跑一下样例，却是大于样例的，第二个更是远大于。然后我就按第一个样例debug，打印一下每个起点长度为4的解的个数，然后我发现路径重复统计了，因此我们必须统计所有节点的入度和出度，然后只有当出度为0也就是终点的$d[x][y][1]=1$，整体思路是深搜得到每个起点能延伸到的终点，从终点回溯，这样能保证每个节点只访问一次的条件下得到答案

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> P;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=1005;

const int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
int a[maxn][maxn],in[maxn][maxn],out[maxn][maxn];
ll d[maxn][maxn][5];
bool vis[maxn][maxn];
int r,c;

bool check(int x,int y){
    if(x<0 || x>=r || y<0 || y>=c) return false;
    return true;
}

void dfs(int x,int y){
    if(vis[x][y]) return;
    vis[x][y]=1;
    if(!out[x][y]) d[x][y][1]=1LL;
    for(int i=0;i<4;i++){
        int xx=x+dx[i],yy=y+dy[i];
        if(!check(xx,yy)) continue;
        if(a[x][y]+1==a[xx][yy]){
            dfs(xx,yy);
            d[x][y][2]=(d[x][y][2]+d[xx][yy][1])%Mod;
            d[x][y][3]=(d[x][y][3]+d[xx][yy][2])%Mod;
            d[x][y][4]=(d[x][y][4]+d[xx][yy][4]+d[xx][yy][3])%Mod;
        }
    }
}

void init(){
    memset(vis,0,sizeof vis);
    memset(d,0,sizeof d);
    memset(out,0,sizeof out);
    memset(in,0,sizeof in);
    for(int i=0;i<r;i++)
        for(int j=0;j<c;j++)
            for(int k=0;k<4;k++){
                int x=i+dx[k],y=j+dy[k];
                if(check(x,y) && a[i][j]+1==a[x][y])
                    out[i][j]++,in[x][y]++;
            }
}

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    //ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    scanf("%d%d",&r,&c);
    for(int i=0;i<r;i++)
        for(int j=0;j<c;j++)
            scanf("%d",&a[i][j]);
    init();
    for(int i=0;i<r;i++)
        for(int j=0;j<c;j++){
            dfs(i,j);
        }
    ll ans=0;
    for(int i=0;i<r;i++)
        for(int j=0;j<c;j++) if(!in[i][j]){
            ans=(ans+d[i][j][4])%Mod;
        }
    printf("%lld\n",ans);
    return 0;
}