pytorch学习之四 简单的二类分类问题

用神经网络解决一个简单的二类分类问题

仍然是看莫烦pytorch的教程。先上代码

from torch.autograd import Variable
import matplotlib.pyplot as plt
import torch.nn.functional as F  #激励函数都在这里
#假数据
n_data = torch.ones( 100,2 )      #数据的基本形态
x0 = torch.normal(2*n_data,1)     #类型0 的x坐标，
                    #torch.normal的意思是从2*datad对应位置的值取期望值，
                    #标准差是第二个参数的正态分布中取值。

y0 = torch.zeros(100)             #0代表是第一个类
x1 = torch.normal( -2*(n_data),1 ) #类型1 
y1 = torch.ones(100)


x,y = Variable(x),Variable(y) #老版本的包装代码。自动微分变量
#注意x，y数据的数据形式一定要像下面一样（torch.cat是合并数据）
x = torch.cat( (x0,x1),0 ).type(torch.FloatTensor)
y = torch.cat( (y0,y1), ).type( torch.LongTensor )
#这是合并两个tensor，cat用后跟着是0的话就是按行来合并，否则为1就是
#按列来合并。而且如果要让Net这种结构能够训练他，必须是这种形式的数据
#x的尺寸应该是torch.Size([200,2])
#y的尺寸应该是torch.Size([200]),x的每一行对应一个样本，y对应标签。

#画图
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()
class Net(torch.nn.Module):  #继承torch.nn.Moudle这个模块，可以调用这个模块的接口
    def __init__(self, n_features,n_hidden,n_output ):     #搭建计算图的一些变量的初始化
        super(Net,self).__init__()  #将self（即自身）转换成Net类对应的父类，调用父类的__init__（）来初始化
        self.hidden = torch.nn.Linear( n_features,n_hidden )
        self.out = torch.nn.Linear( n_hidden,n_output )
        
              
    def forward(self,x):      #前向传播，搭建计算图的过程
        x = F.relu(self.hidden(x))
        x = self.out(x)
        return x
    
net = Net( n_features=2,n_hidden=10,n_output=2 )
optimizer=torch.optim.SGD(net.parameters(),lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()

plt.ion()   # 画图
plt.show()
for t in range(100):
    out = net(x)
    loss = loss_func(out,y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if t % 2 == 0:
        plt.cla()
        # 过了一道 softmax 的激励函数后的最大概率才是预测值
        prediction = torch.max(F.softmax(out), 1)[1]
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = sum(pred_y == target_y)/200.  # 预测中有多少和真实值一样
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)
plt.ioff()  # 停止画图
plt.show()

整体框架跟回归问题差不多。

构建伪数据

n_data = torch.ones( 100,2 )      #数据的基本形态
x0 = torch.normal(2*n_data,1)     #类型0 的x坐标，
                    #torch.normal的意思是从2*datad对应位置的值取期望值，
                    #标准差是第二个参数的正态分布中取值。

y0 = torch.zeros(100)             #0代表是第一个类
x1 = torch.normal( -2*(n_data),1 ) #类型1 
y1 = torch.ones(100)

x,y = Variable(x),Variable(y) #老版本的包装代码。自动微分变量

构建两类数据，torch.normal是正态分布函数，它会生成一个与n_data尺寸相同的tensor，每个元素会以n_data中对应元素的值为期望，1为标准差,最后再把两个类型的xi,yi按行连接到一个tensor里面，
值得注意的是y值。并没有修改成one hot的形式。，这是因为最终的代价函数选择的是
torch.nn.CrossEntropyLoss()，交叉熵代价。这里有一篇博文，对这个代价函数有详细的介绍
https://www.cnblogs.com/fledlingbird/p/9879457.html
简单的说，交叉熵函数定义

其中yi’对应样本类别的独热码形式，yi对应神经网络输出层的形式
如

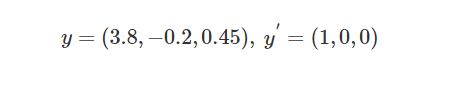
可以看到计算的值，还要通过softmax映射到0-1之间，也就是将输出映射出一个概率值，如下图

对于pytorch中的torch.nn.CrossEntropyLosss()，其实one hot编码，最后交叉熵的结果是

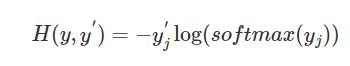
除了样本输出特征为1的那一项，其他的项都为0，那么其实我只需要知道是样本输出特征值为1个好了，换句话说，只需要知道label就好了，。
oss = nn.CrossEntropyLoss( )
loss（output, label） label就对应上式的j。

也就是说计算CrossEntropyLoss, 只需要一个label，以及一个样本输出向量就可以了

• 输出值不需要进行softmax函数
• 标签不需要进行独热编码

搭建神经网络以及梯度下降

net = Net( n_features=2,n_hidden=10,n_output=2 )
optimizer=torch.optim.SGD(net.parameters(),lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()

plt.ion()   # 画图
plt.show()
for t in range(100):
    out = net(x)
    loss = loss_func(out,y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    

这部分几乎跟做线性回归的时候一模一样，只不过代价函数给换成了交叉熵，这种函数在分类里面用的很多。

绘图过程

plt.ion()   # 画图
plt.show()
for t in range(100):
...
    
    if t % 2 == 0:
        plt.cla()
        # 过了一道 softmax 的激励函数后的最大概率才是预测值
        prediction = torch.max(F.softmax(out), 1)[1]
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = sum(pred_y == target_y)/200.  # 预测中有多少和真实值一样
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)
plt.ioff()  # 停止画图
plt.show()

F.softmax(out) 将out向量转化成一个概率分布，
torch.max( A,1)表示返回一列中最大的那个值，和它所在的行号
torch.max( A,1)[1]就是最大值所在列号的索引值，也就是label值。
所以prediction = torch.max(F.softmax(out), 1)[1]会返回预测的label编号

pred_y = prediction.data.numpy().squeeze()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = sum(pred_y == target_y)/200.  #计算预测精度

pred_y, target_y分别是输出的类别，以及样本的类别。都转成numpy形式，为了方便计算和绘图 画图的时候，点坐标还是样本的输入特征值，颜色关联的是预测向量，那么颜色将会关联两个类别。

sum( pred_y == target_y ) 表示一个bool数组，如果预测类别和样本类别相同，该位置置1，否则置0 。

       plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

最后打印一个精度值。结束