【蓝桥杯】 算法训练 数字三角形

历届试题 数字三角形

问题描述
在下面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。 三角形的行数大于1小于等于100，数字为 0–99。

输入格式：
第一行为一个整数n，表示接下来将要输入的三角形行数
接下来是n行，每行输入当前行数的个数个数

输出格式：输出一个数字，表示最大和

样例输入：如上图

样例输出：30
数据说明：最大路径为（7-3-8-7-5）从上至下

---

—— 初入江湖之动态规划 ——

---

分析：
这是一道经典的动态规划问题，我们还是从最浅显的算法出发，由浅到深慢慢研究
首先最容易想到的，就是暴力搜索算法。我们先用一个二维数组map来存放上面的数字三角形，于是有:
map[1][1]=7
map[2][1]=3 map[2][2]=8
map[3][1]=8 map[3][2]=1 map[3][3]=0
……
然后我们假设，这里有一个名为dfs(x,y)的函数，该函数能从上述三角形中位置为(x,y)处出发，往其下自动寻找最大路径和，并返回这个和。那么对于题目输入的任何数字三角形，我们只需要输出dfs(1,1)即可
接下来，我们的重点就落在了如何设计这个dfs函数上，这样的转换和汉诺塔问题挺像的，我们慢慢分析
我们看图可以知道，在map[1][1]下面，只有两条路：要么选择map[2][1]，要么选择map[2][2]
也就是说，最大路径应该在这两者之间产生，那么我们为了选择最大路径和，当然是选较大的，即：
return max( dfs(2,1),dfs(2,2) ) + map[1][1]
同样地，在dfs(2,1)和dfs(2,2)中也一样，其分别也是选择在其下方中较大的，于是我们可以得出递归式：

int dfs(int i,int j)
{	
	return max( dfs(i+1,j),dfs(i+1,j+1) ) + map[i][j];  
}

上述递归式中给出了程序在自顶向下进行寻找最大路径和的过程，但是却没有给出中止条件
细想，当i走到了最后一行时（即i==n）时，我们的dfs函数就不能再往下dfs下去了，那么此时我们就直接返回值就行了，于是可以得到采用递归方法进行求解的完整代码为：

#include
using namespace std;

const int N=105;
int n,map[N][N];
int dfs(int i,int j)
{
	if(i==n) return map[i][j];
	else return max(dfs(i+1,j),dfs(i+1,j+1))+map[i][j];
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin>>map[i][j];
	cout<<dfs(1,1)<<endl;
	return 0;
}

提交这个代码上去，只得了57分(过了4/7的数据)
得到这样的结果是很正常的。要知道，递归是需要使用大量堆栈上的空间，极易造成栈溢出。而通常在递归树超过了50层的时候，就会消耗大量的时间和空间。并且根据前面“动态规划之斐波那契数列”对递归算法的分析，我们知道递归做了大量的重复工作。因此，为了能通过所有的测试数据，我们就需要用一个数组来保存前面已经算出的结果，从而使得递归变为递推

根据dfs算法的思路，程序总会dfs到最后一行，然后开始选择最大值，那么我们的表格也应该是从最后一行开始填写，如下图所示，我们首先把最下面一行填入表格中：

然后开始倒数第二行的填写。先分析数字2，2可以和最后一行4相加，也可以和最后一行的5相加，但是很显然和5相加要更大一点，结果为7，我们此时就可以将7保存起来；然后分析数字7，7可以和最后一行的5相加，也可以和最后一行的2相加，很显然和5相加更大，结果为12，因此我们将12保存起来。以此类推……最终可以得到下面这张图：

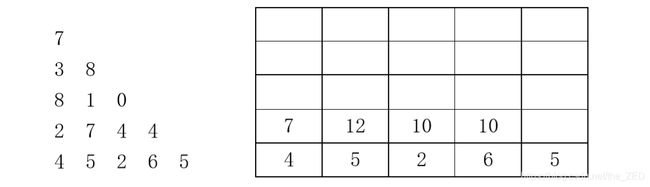
然后按同样的方法填写倒数第三行和倒数第四行，直至第一行，我们可以依次得到如下结果：

如果设maxSum(i,j)表示坐标为(i,j)的位置通向最后一行所寻找到的最大路径和
那么根据上面的推导过程，我们可以得到这里面的递推公式为：
maxSum[ i ][ j ] = max( maxSum[ i+1 ][ j ],maxSum[ i+1 ][ j+1 ] ) + map[ i ][ j ];
根据这样的思路写出的完整代码如下：

#include
using namespace std;
const int N=105;
int n,map[N][N],maxSum[N][N];
void dp()
{
	for(int i=1;i<=n;i++) maxSum[n][i]=map[n][i];
	for(int i=n-1;i>=1;i--)
		for(int j=1;j<=i;j++)
			maxSum[i][j] = max(maxSum[i+1][j],maxSum[i+1][j+1]) + map[i][j];
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin>>map[i][j];
	dp();
	cout<<maxSum[1][1]<<endl;
	return 0;
}

实际上，我们没有必要用一个maxSum[N][N]数组来进行递推，我们就在map[N][N]数组上就行，即：

#include
using namespace std;

const int N=105;
int n,map[N][N];
void dp()
{
	for(int i=n-1;i>=1;i--)
		for(int j=1;j<=i;j++)
			map[i][j] = max(map[i+1][j],map[i+1][j+1]) + map[i][j];
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin>>map[i][j];
	dp();
	cout<<map[1][1]<<endl;
	return 0;
}

---

—— 翻山越岭之内存优化 ——

---

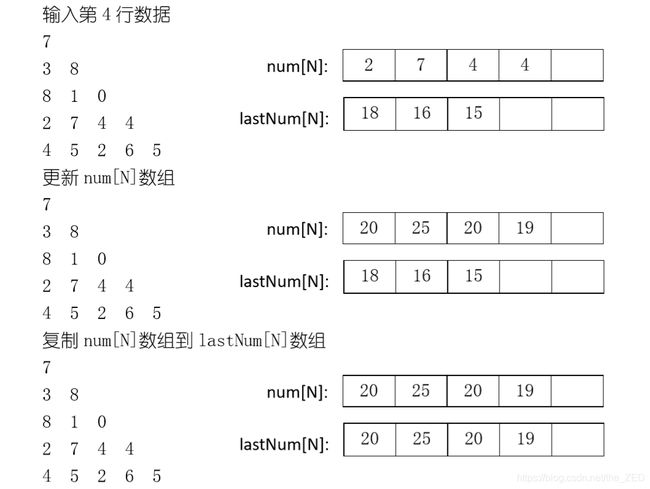
更进一步，我们甚至连二维矩阵都不需要，直接用两个一维数组就行，一个一维数组num[N]用于存放当前输入的某一行数字；另一个一维数组lastNum[N]用于存放对某行进行操作后的情况。显然，这种处理办法是基于对输入的数字三角形进行行处理而得到的，但是题目给出的数字三角形的输入是从上往下进行的，而上面介绍的所有求解办法都是从下往上进行的。因此，在介绍用两个一维数组进行处理的办法前，需要先介绍下从上往下解答的算法。老规矩，从填表开始：

第一次，由于第一行只有一个数字，因此得到的表格如下：

第二次，此时往下走，由于出发点只有一个数字7，且终点也只有两个数字（分别为3和8），因此从第一行往二行走的办法只有两条，无需选择，于是得到的表格如下：

第三次，此时出发点就有两个了，我们把目光主要放在第三行，比如现在针对第三行第一列的数字8，其只能由其上方的数字3走来，于是得到第三行第一列的路径和为7+3+8=18；然后看第三行第二列的数字1，其可以由其上方的数字3和数字8走来，但是显然，从数字8走来会使得路径和更大，因此第三行第二列的路径和为7+8+1=16；最后是第三行第三列的数字0，其也只能从其上方的数字8走来，于是得到第三行第三列的路径和为7+8+0=15。最终得到的表格如下：

按照这样的思路继续填表，得到的表格内容依次如下：

最终，表格的最下边那一行装填了从整个数字三角形顶端到底端各个出口的最大路径和。如果我们要求解这其中的最大值就还需要写一个取数组maxSum[n][n]={24，30，27，26，24}最大值的函数
实际上，在上面的填表过程中，动态转移方程变成了（设原始数据存放在map[N][N]中，所填的表格为maxSum[N][N]）：
maxSum[ i ][ j ] = max( maxSum[ i-1 ][ j-1 ],maxSum[ i-1 ][ j ] ) + map[ i ][ j ]
同样地，这里我们也可以不用maxSum[N][N]数组，而是直接在map[N][N]中进行动态转移变换：
map[ i ][ j ] = max( map[ i-1 ][ j-1 ],map[ i-1 ][ j ] ) + map[ i ][ j ]

采用这种方法求解本题题的完整代码如下：

#include
using namespace std;

const int N=105;
int n,map[N][N];
void dp()
{
	for(int i=2;i<=n;i++)
		for(int j=1;j<=i;j++)
			map[i][j] = max(map[i-1][j-1],map[i-1][j]) + map[i][j];
}
int maxValue()
{
	int max=map[n][1];
	for(int i=2;i<=n;i++)
		if(map[n][i]>max) max=map[n][i];
	return max;
}

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin>>map[i][j];
	dp();
	cout<<maxValue()<<endl;
	return 0;
}

---

—— 登峰造极之递推求解 ——

---

上面的内容是个小插曲，主要是为了让大家熟悉从上往下解题的方法。别忘了我们的初衷是要优化程序的空间为两个一维数组，下面开始介绍具体的做法。同样地，我们依然填表开始，如下：

首先是将第一行的数据输入num[N]数组，如下：

然后再更新num[N]数组中的某个元素num[i]为max( lastNum[ i ],lastNum[ i-1 ] )+num[ i ]，如下：

最后将num[N]数组中的内容复制到lastNum[N]数组中，如下：



接下来到了第2行，同样地先将整行数据输入num[N]数组中，即num[N]={3，8}，如下：

然后将num[N]数组中的某个元素num[i]更新为max( lastNum[i],lastNum[i-1] )+num[i]，如下：

最后将num[N]数组中的内容复制到lastNum[N]数组中，如下：

然后按照这样的方式不断更新lastNum[N]数组，如下：

最终，在lastNum[N]数组中存储的就是该数字三角形自顶向下往金字塔底部每个数字出去的最大路径和，为了取得这之间的最大值我们就还需要写一个对某数组求解最大值的函数
此外还需要提的一点是，上述算法我们需要将num[N]数组中的内容更新到lastNum[N]数组中。在上面的演示中我采用的是复制过去的方式。我们知道，复制某个数组到另一个数组是一个线性的时间复杂度，那么在具有n行的数字金字塔中，上述算法在复制数组上的时间复杂度就变成了O(n2/2)。如果为了降低空间复杂度而使得程序的时间复杂度增加，这样是得不偿失的。但是我们可以采用指针来完成这项工作！
即通过用指针来改变指向的数组即可，这样就避免了数组的复制，从而使得时间复杂度不变
下面直接给出使用此方法求解本题的完整代码：

#include
using namespace std;

const int N=105;
int n,*num,*lastNum,ary1[N],ary2[N];
void dp()
{
	num=ary1,lastNum=ary2;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			cin>>num[j];
			num[j]=max(lastNum[j],lastNum[j-1])+num[j];
		}
		swap(num,lastNum);
	}

}
int maxValue()
{
	int max=lastNum[1];
	for(int i=2;i<=n;i++)
		if(lastNum[i]>max) max=lastNum[i];
	return max;
}

int main()
{
	cin>>n;dp();
	cout<<maxValue()<<endl;
	return 0;
}

---