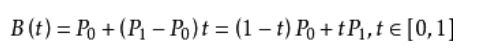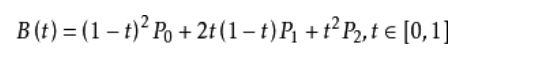Unity 工具类 之 贝塞尔 Bezier 曲线

Unity 工具类 之 贝塞尔 Bezier 曲线

 

目录

Unity 工具类 之 贝塞尔 Bezier 曲线

一、简单介绍

二、原理与分类

三、公式与原理图演示

五、注意事项

六、样例使用步骤（三次贝塞尔方程曲线）

七、代码

---

 

一、简单介绍

贝塞尔曲线是最基本的曲线，一般用在计算机 图形学和 图像处理。贝塞尔曲线可以用来创建平滑的曲线的道路、 弯曲的路径就像 祖玛游戏、 弯曲型的河流等。

 

二、原理与分类

贝塞尔曲线返回点的贝塞尔函数，使用线性插值的概念作为基础。

 一条贝塞尔曲线是由一组定义的控制点 P0到 Pn，在 n 调用它的顺序 (n = 1 为线性，2 为二次，等.)。第一个和最后一个控制点总是具有终结点的曲线;然而，中间两个控制点 (如果有的话) 一般不会位于曲线上 。

（1）贝塞尔曲线包含两个控制点即 n = 2 称为线性的贝塞尔曲线

（2）贝塞尔曲线包含三个控制点即 n = 3 称为二次贝塞尔曲线

（3）贝塞尔曲线包含四个控制点即 n = 4，所以称为三次贝塞尔曲线。

三、公式与原理图演示

1.线性贝塞尔公式：

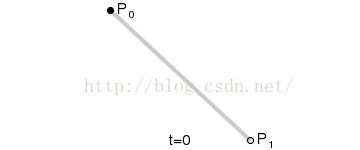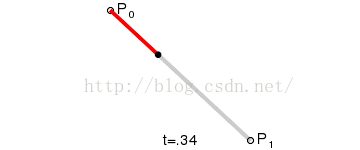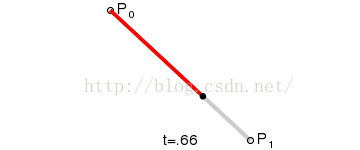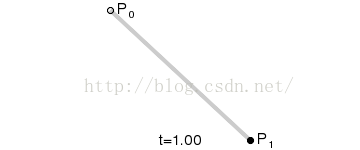
给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。这条线由下式给出：

其等同于线性插值。

2.二次贝塞尔公式：

二次方贝兹曲线的路径由给定点P0、P1、P2控制，这条线由下式给出：

3.三次贝塞尔方程：

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是用来充当控制点。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。

曲线的参数形式为：

4.一般参数形式的贝塞尔方程：

 N阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：

如上公式可如下递归表达： 用表示由点P0、P1、…、Pn所决定的贝兹曲线。

 

五、注意事项

1、通过两个低阶的贝塞尔曲线插值的堆叠总能够获得更高阶的贝塞尔曲线，通俗的来说通过对两条低阶的贝塞尔曲线插值，你可以求得一条高一阶的贝塞尔曲线。

2、二次贝塞尔曲线是点对点的两个线性贝塞尔曲线的线性插值，三次贝塞尔曲线是两条二次贝塞尔曲线的线性插值。
 

六、样例使用步骤（三次贝塞尔方程曲线）

1、打开Unity，新建一个场景，里面 添加一些球体，作为贝塞尔曲线点，如下图

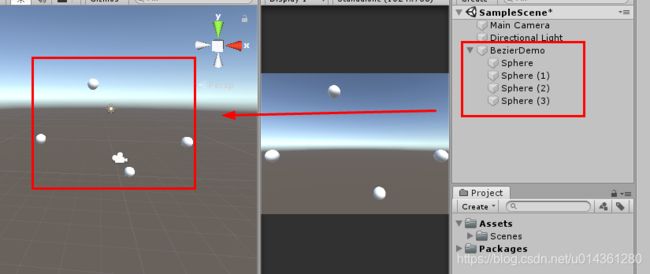
2、新建贝塞尔接口脚本，和调用脚本，调用脚本挂载到 BezierDemo 物体上，并把球体依次赋值，如下图

3、运行场景，三次贝塞尔曲线效果，如下图

 

七、代码

1、BezierDemo 代码

using UnityEngine;

[RequireComponent(typeof(LineRenderer))]
public class BezierDemo : MonoBehaviour
{
    // 三次贝塞尔控制点
    public Transform[] controlPoints;

    // LineRenderer 
    private LineRenderer lineRenderer;
    private int layerOrder = 0;

    // 设置贝塞尔插值个数
    private int _segmentNum = 50;   


    void Start()
    {
        if (!lineRenderer)
        {
            lineRenderer = GetComponent();
        }
        lineRenderer.sortingLayerID = layerOrder;

    }

    void Update()
    {

        DrawThreePowerCurve();

    }


    Vector3[] points3;
    void DrawThreePowerCurve()
    {
        // 获取三次贝塞尔方程曲线
        points3 = BezierUtils.GetThreePowerBeizerList(controlPoints[0].position, controlPoints[1].position, controlPoints[2].position, controlPoints[3].position, _segmentNum);
        // 设置 LineRenderer 的点个数，并赋值点值
        lineRenderer.positionCount = (_segmentNum);
        lineRenderer.SetPositions(points3);

    }

}

 

2、BezierUtils 代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class BezierUtils
{

    /// 

    /// 线性贝塞尔曲线，根据T值，计算贝塞尔曲线上面相对应的点
    /// 
    /// T值
    /// 起始点
    /// 控制点
    /// 根据T值计算出来的贝赛尔曲线点
    private static Vector3 CalculateLineBezierPoint(float t, Vector3 p0, Vector3 p1)
    {
        float u = 1 - t;
         
        Vector3 p = u * p0;
        p +=  t * p1;
    

        return p;
    }

    /// 

    /// 二次贝塞尔曲线，根据T值，计算贝塞尔曲线上面相对应的点
    /// 
    /// T值
    /// 起始点
    /// 控制点
    /// 目标点
    /// 根据T值计算出来的贝赛尔曲线点
    private static Vector3 CalculateCubicBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2)
    {
        float u = 1 - t;
        float tt = t * t;
        float uu = u * u;

        Vector3 p = uu * p0;
        p += 2 * u * t * p1;
        p += tt * p2;

        return p;
    }

    /// 

    /// 三次贝塞尔曲线，根据T值，计算贝塞尔曲线上面相对应的点
    /// 
    /// 插量值
    /// 起点
    /// 控制点1
    /// 控制点2
    /// 尾点
    /// 
    private static Vector3 CalculateThreePowerBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
    {
        float u = 1 - t;
        float tt = t * t;
        float uu = u * u;
        float ttt = tt * t;
        float uuu = uu * u;

        Vector3 p = uuu * p0;
        p += 3 * t * uu * p1;
        p += 3 * tt * u * p2;
        p += ttt * p3;

        return p;
    }


    /// 

    /// 获取存储贝塞尔曲线点的数组
    /// 
    /// 起始点
    /// 控制点
    /// 目标点
    /// 采样点的数量
    /// 存储贝塞尔曲线点的数组
    public static Vector3[] GetLineBeizerList(Vector3 startPoint,  Vector3 endPoint, int segmentNum)
    {
        Vector3[] path = new Vector3[segmentNum];
        for (int i = 1; i <= segmentNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pixel = CalculateLineBezierPoint(t, startPoint, endPoint);
            path[i - 1] = pixel;
            Debug.Log(path[i - 1]);
        }
        return path;

    }

    /// 

    /// 获取存储的二次贝塞尔曲线点的数组
    /// 
    /// 起始点
    /// 控制点
    /// 目标点
    /// 采样点的数量
    /// 存储贝塞尔曲线点的数组
    public static Vector3[] GetCubicBeizerList(Vector3 startPoint, Vector3 controlPoint, Vector3 endPoint, int segmentNum)
    {
        Vector3[] path = new Vector3[segmentNum];
        for (int i = 1; i <= segmentNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pixel = CalculateCubicBezierPoint(t, startPoint,
                controlPoint, endPoint);
            path[i - 1] = pixel;
            Debug.Log(path[i - 1]);
        }
        return path;

    }

    /// 

    /// 获取存储的三次贝塞尔曲线点的数组
    /// 
    /// 起始点
    /// 控制点1
    /// 控制点2
    /// 目标点
    /// 采样点的数量
    /// 存储贝塞尔曲线点的数组
    public static Vector3[] GetThreePowerBeizerList(Vector3 startPoint, Vector3 controlPoint1, Vector3 controlPoint2 , Vector3 endPoint, int segmentNum)
    {
        Vector3[] path = new Vector3[segmentNum];
        for (int i = 1; i <= segmentNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pixel = CalculateThreePowerBezierPoint(t, startPoint,
                controlPoint1, controlPoint2, endPoint);
            path[i - 1] = pixel;
            Debug.Log(path[i - 1]);
        }
        return path;

    }
}