拉格朗日乘子法及浅谈Svm
拉格朗日乘子法是干啥的
简单点来说给你一个z=ƒ(x,y),求这个函数的极值点(x0,y0),但是我有个约束条件,这个约束条件是φ(x,y)=0。就是说你找到的极值点必须同时满足φ(x0,y0)=0.
在数学最优问题中,拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法,下面的讨论中我们暂且先只考虑一个约束条件。
拉格朗日乘子法证明
我们把z=ƒ(x,y)投影到xOy平面,ƒ(x,y)=Ci(i=1,2…n)是一系列的等值线。对于φ(x,y)=0本身就是二维的,因为没有变量Z,所以直接画在xOy平面上。

(图片来源百度百科)
可知在φ(x,y)=0的约束条件下,图中的交点就是我们x,y所可以取的值。我们要在这些交点里面找到某一个点,这个点是f(x,y)的极值点。其实图中的等值线有很多,与φ(x,y)=0的交点构成一条闭合曲线,这条曲线就是φ(x,y)=0,这很容易想到。图中只花了一些代表性的的等值线和φ(x,y)=0。M1和M3比较特殊是切点,其余的点和M2都是普通的交点,只标注一个M2.
现在我们要做的就是在这些交点里面找到一个点,这个点是f(x,y)的极值。你可能会问不应该是z=f(x,y)的极值么,怎么变成f(x,y)的极值了。没错,但是Z在里是关于x,y的应变量,与x,y有关。也就是找到f(x,y)的极值,这很容易想到。
小思考
现在的问题是如何找到这个极值点。因为这个约束条件很烦,我们不能像以往那样直接令f(x,y)对x,y的偏导数为0去直接求极值点,因为这个约束在,我们如果直接求得话,有可能求出来得x,y不符合这个约束条件。有人就会说,那我先求出来,然后再把结果带入到φ(x,y)=0看看成不成立不就行了。没错,这样做在一些简单得数学问题中是最常用的方法,但是往往我们需要解决得问题很复杂,极值点可能有非常多个一个一个试比较耗费事件,我们不希望这样做。
几何的角度分析
对于这个图们假设随着x,y增大等值曲线得值也增大。
那么从M2到M3这一段可以看出,值在不断增大,从M3到M1的值不断的减小。那我们就认为在M3这一点就是个转折点,也就是我们所说的极值点。很容易看出在这一点f(x,y)的法向量和φ(x,y)的法向量是平行的。我们知道某点的法向量就是梯度向量,所以说在极值点这两个函数的梯度是平行的。这是我们从几何的角度去看的。
数学分析角度
下面我们从分析的角度去分析。
φ(x,y)我们可以写成隐函数的形式y=y(x),在极值点的话有y0=y(x0).那么在极值点处的z=ƒ(x,y)可以写成z=ƒ(x,y(x))。可知z在这个点对x求偏导是0。
推导过程用到了复合函数求导和隐函数求导,得到下面得过程:
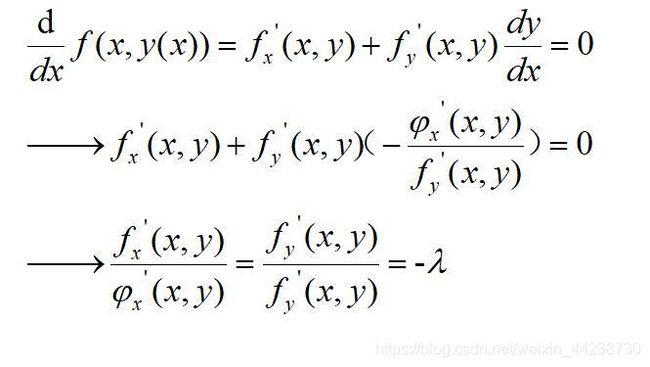
我们通过数学证明了在极值点处两个梯度是平行的,并且我们记这个比值为-λ。
好的我们现在回头看看原来的问题,在φ(x,y)=0的条件之下求ƒ(x,y)的极值点(x0,y0)就转换成了求某一个点使这个两个函数在这个点的梯度平行。这样我们就把约束问题转换成了非约束问题。
拉格朗日函数
对于上面的转换我们可以写成L(x,y,λ)=f(x,y)+λφ(x,y)。这个函数我们称为拉格朗日函数,λ称为拉格朗日乘子。我们只要求得这个函数得驻点,也就是梯度为0的点,就是求出了问题转换前得极值点。为什么呢?其实很简单我只要写出来你就知道了。对于求拉格朗日函数的驻点我们可以很自然的写出下面的式子 
可以看到这个式子就是我们之前得到的梯度平行的式子。
就是说,在没转换之前我们对x,y的取值受到了φ(x,y)=0的约束,我们的x,y必须在这个条件之下才能够进行取值,转换之后我们的x,y取值不受约束,我么只需要像以前那样使偏导数为0来求极值,只不过这里多了一个λ
你可能想问为什么转换之后,x,y得取值就不受约束了呢?拉格朗日乘子妙就妙在,当你转换成拉格朗日函数之后,对其求解的过程,就自动的把那些不符合φ(x,y)=0的点去掉了。就比如上面对拉格朗日函数求导时,你自然得就符合了之前得约束条件。
并且拉格朗日乘子法可以对多个约束条件进行求解。之前我们把一个约束条件的拉格朗日函数写成L(x,y,λ)=f(x,y)+λφ(x,y),进而我们可以推广到对对于n个约束条件的拉格朗日函数的写法
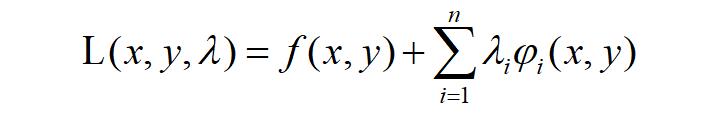
SVM中的拉格朗日乘子法(浅谈)
在支持向量机得求解优化得过程,我们就用到了拉格朗日乘子法。拉格朗日求到的是极值,你怎么知道求到的是极大值还是极小值呢?就拿SVM来说,我们希望求到的是最小值,你如何保证求值结果不是极大值或者是局部极小值。对于SVM来说是一个凸二次规划问题,也就是凸函数的求解,凸函数的性质就是局部最小即全局最小,而且没有极大值。这涉及到最优化理论的问题,不再深入。并且我这里也只是简单的引出一下SVM,拉格朗日乘子法只是其中一小部分。后续我会具体的写一些关于SVM的知识。